2018-2019学年山西省长治二中高二上学期期末考试数学（理）试题 解析版

2018-2019学年山西省长治二中高二上学期期末考试数学（理）试题 解析版

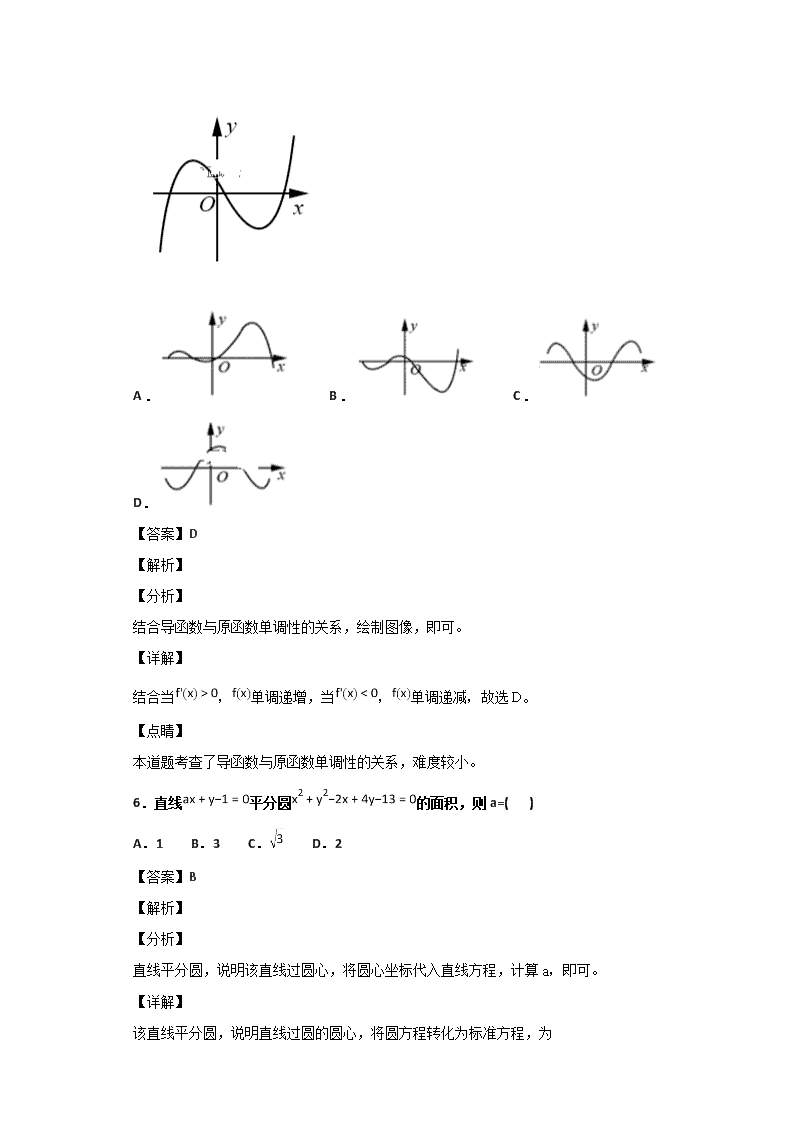
绝密★启用前 山西省长治二中2018-2019学年高二上学期期末考试数学（理)试卷 评卷人 得分 一、单选题 ‎1．已知命题：，：，则是的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】A ‎【解析】‎ 分析：根据题意，求得，即可利用集合之间的关系，判定得到结论.‎ 详解：由题意可得，解得，‎ 则“”是“”成立的充分不必要条件，‎ 即“”是“”成立的充分不必要条件，故选A.‎ 点睛：本题考查了充分不必要条件的判定，其中正确求解命题，利用集合之间的大小关系是解答的关键，着重考查了学生的推理与运算能力.‎ ‎2．双曲线的实轴长是 A．2 B． C．4 D．4‎ ‎【答案】C ‎【解析】‎ 试题分析：双曲线方程变形为，所以，虚轴长为 考点：双曲线方程及性质 ‎3．某三棱锥的三视图如图所示，则该三棱锥的体积是( )‎ ‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由三视图判断底面为等腰直角三角形，三棱锥的高为2，则，选B.‎ ‎【考点定位】三视图与几何体的体积 ‎4．已知函数的导函数为，则的解集为( )‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 计算导函数，解不等式，即可。‎ ‎【详解】‎ 计算导函数得到,,解得x的范围为，故选C。‎ ‎【点睛】‎ 本道题考查了导函数计算方法，考查了不等式的计算，难度较小。‎ ‎5．函数的导函数的图象如图所示，则函数的图象可能是( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 结合导函数与原函数单调性的关系，绘制图像，即可。‎ ‎【详解】‎ 结合当，单调递增，当，单调递减，故选D。‎ ‎【点睛】‎ 本道题考查了导函数与原函数单调性的关系，难度较小。‎ ‎6．直线平分圆的面积，则a=( )‎ A．1 B．3 C． D．2‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 直线平分圆，说明该直线过圆心，将圆心坐标代入直线方程，计算a，即可。‎ ‎【详解】‎ 该直线平分圆，说明直线过圆的圆心，将圆方程转化为标准方程，为 ‎，圆心坐标为，代入直线方程，得到 ‎，故选B。‎ ‎【点睛】‎ 本道题考查了直线与圆的位置关系，考查了参数计算方法，难度较小。‎ ‎7．已知双曲线C： (a>0，b>0)的一条渐近线方程为y＝x，且与椭圆有公共焦点，则C的方程为(　　)‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由双曲线的渐近线方程可得=，① 由椭圆的焦点坐标（），即c=3 a2+b2=9，②，解方程可得a，b的值，得到双曲线的方程．‎ ‎【详解】‎ 双曲线C：=1（a＞0，b＞0）的一条渐近线方程为y＝x，‎ 可得=，①‎ 椭圆的焦点为（±3，0），‎ 可得c=3，即a2+b2=9，②‎ 由①②可得a=2，b= ，‎ 则双曲线的方程为．‎ 故选：B．‎ ‎【点睛】‎ 本题考查双曲线的方程的求法，注意运用双曲线的渐近线方程和椭圆的焦点，考查运算能力，属于基础题．‎ ‎8．若在上是减函数，则的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先对函数进行求导，根据导函数小于0时原函数单调递减即可得到答案．‎ ‎【详解】‎ 由题意可知，在x∈（﹣1，+∞）上恒成立，‎ 即b＜x（x+2）在x∈（﹣1，+∞）上恒成立，‎ 由于y=x（x+2）在（﹣1，+∞）上是增函数且y（﹣1）=﹣1，所以b≤﹣1，‎ 故选：C．‎ ‎【点睛】‎ 函数单调性与导函数的符号之间的关系要注意以下结论 ‎（1）若在内，则在上单调递增（减）．‎ ‎（2）在上单调递增（减） （）在上恒成立，且在的任意子区间内都不恒等于0．（不要掉了等号．）‎ ‎（3）若函数在区间内存在单调递增（减）区间，则在上有解．（不要加上等号．）‎ ‎9．如图，已知直线与抛物线交于A，B两点，且OA⊥OB,OD⊥AB交AB于点D，点D的坐标（4，2），则p=( )。‎ A．3 B． C． D．4‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 结合D点坐标,计算直线方程,代入抛物线方程,建立一元二次方程,结合,建立等式,结合根与系数的关系,代入,计算p，即可。‎ ‎【详解】‎ 设出该直线方程为，得到因为D O点到该直线的距离为，结合点到直线距离公式，得到 解得，‎ 将直线方程代入抛物线方程，得到，解得 ‎，结合得到 ‎，得到,解得,故选C.‎ ‎【点睛】‎ 本道题考查了直线与抛物线位置关系，考查了直线方程计算，难度偏难。‎ ‎10．函数的图像经过四个象限，则实数的取值范围是( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 本道题计算导函数，结合a取不同范围，判定是否满足条件，进而得出a的范围，结合导函数与原函数的单调性关系，结合题意，判定极值满足的条件，进而得出a的确定范围，即可。‎ ‎【详解】‎ 求导得到 若则在递增，在 递减，可知，故函数不会经过第三、四象限，因而 得到在递减，在其他区间递增，要使得经过四个象限，则要求 得到a的范围是，故选D。‎ ‎【点睛】‎ 本道题考查了导函数与原函数的单调性关系，难度偏难。‎ ‎11．已知椭圆：的左右焦点分别为，为椭圆上的一点与椭圆交于。若的内切圆与线段在其中点处相切，与切于，则椭圆的离心率为( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 结合题意,证明得到三角形为等边三角形,对三角形运用余弦定理,计算离心率,即可.‎ ‎【详解】‎ 结合题意可知结合内切圆的性质,可得,结合椭圆的性质 ‎,而,所以,结合内切圆的性质,可以得出结合椭圆的性质,可得,由此可知为等边三角形,进而得出,对三角形运用余弦定理,得到 ‎,解得,故选D.‎ ‎【点睛】‎ 本道题考查了椭圆基本性质,考查了余弦定理,难度偏难.‎ ‎12．已知函数在上 可导，其导函数为，若满足：当时，，，则下列判断一定正确的是 ( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 本道题构造函数,结合导函数,判定单调性,判定对称轴,得到大小关系,即可.‎ ‎【详解】‎ 构造函数,计算导函数得到 结合题意得到当时,当时,‎ 所以在单调递增,在单调递减,‎ 而,所以关于对称,‎ 故,得到,故选D.‎ ‎【点睛】‎ 本道题考查了导函数判定原函数单调性,考查了函数对称轴判定,难度偏难.‎ 第II卷（非选择题)‎ 请点击修改第II卷的文字说明 评卷人 得分 二、填空题 ‎13．命题，使得”的否定为____。‎ ‎【答案】都有 ‎【解析】‎ ‎【分析】‎ 改为，改为，即可。‎ ‎【详解】‎ 改为，改为，故命题的否定为都有 ‎【点睛】‎ 本道题考查了命题的否定改写，关键抓住改为，改为，属于较容易的题。‎ ‎14．函数的极值点是____。‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 令导数为0，计算x，即可。‎ ‎【详解】‎ 解得 ‎【点睛】‎ 本道题考查了函数导数计算方法，关键抓住，即可，难度较容易。‎ ‎15．已知F1、F2分别为双曲线的左、右焦点，点P为双曲线右支上的一点，满足，且，则该双曲线离心率为 ． ‎ ‎【答案】.‎ ‎【解析】‎ 试题分析：，在中，设，‎ 则，.‎ 考点：双曲线的离心率.‎ ‎16．已知a、b、c是实数，方程的三个实数根可以作为椭圆、双曲线、抛物线的离心率，则的取值范围是____。‎ ‎【答案】(5，+)‎ ‎【解析】‎ ‎【分析】‎ 本道题结合题意，得出c与a,b的关系，结合题意，构造不等式，转化为线性规划的题，计算最值，计算范围，即可。‎ ‎【详解】‎ 构造函数,因为一个根为抛物线的离心率,可知 ‎,解得,因为三个实数根分别为椭圆、双曲线和抛物线的离心率，可知一个根大于0，小于1，一个根大于1，一个根为1，绘制图像 计算导函数设导函数为0时两个根为m,n，依据图像可知 ‎，所以得到且而 ‎，建立不等式得到 ‎，绘制可行域，可得 而可以看成点到距离的平方和，所以A可以使得取得最小值，‎ 所以最小值为，故写成集合的形式为 ‎【点睛】‎ 本道题考查了线性规划问题，关键在于结合题意，建立不等式，转化为线性规划进行解决，难度偏难。‎ 评卷人 得分 三、解答题 ‎17．已知命题 “方程表示焦点在轴上的椭圆”，命题 “方程表示双曲线”.‎ ‎（1）若是真命题，求实数的取值范围；‎ ‎（2）若“或”是真命题，求实数的取值范围.‎ ‎【答案】（1）（2）或.‎ ‎【解析】试题分析：‎ ‎(1)由题意得到关于实数k的不等式组，求解不等式组有.‎ ‎(2)由题意可得，命题至少一个是真命题，即一真一假或全为真.据此得到关于实数k的不等式组，求解不等式组可得实数的取值范围是或.‎ 试题解析：‎ ‎（1）命题：“方程表示焦点在轴上的椭圆”，则，解得.‎ ‎（2）命题 “方程表示双曲线”，则，解得或.‎ 若“或”是真命题，则至少一个是真命题，即一真一假或全为真.‎ 则或或，‎ 所以或或或.‎ 所以或.‎ ‎18．如图，四面体ABCD中，O是BD的中点，AB=AD=2，.‎ ‎（1）求证：AO⊥平面BCD；‎ ‎（2）求异面直线AD与BC所成角的余弦值的大小；‎ ‎【答案】（1）详见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)分别证明AO垂直OC,垂直BD,结合直线与平面垂直判定,即可.(2)建立空间坐标系，分别计算各点坐标，结合向量数量积公式，计算，即可。‎ ‎【详解】‎ 解：（1）连接OC，∵BO=DO，AB=AD，∴AO⊥BD，‎ ‎∵BO=DO，BC=CD，∴CO⊥BD，‎ 在△AOC中，由题设知AO=，,AC=，‎ ‎∴AO2+CO2=AC2， ‎ ‎∴∠AOC=90°，即AO⊥OC，‎ ‎∵AO⊥BD，BD∩OC=O， ‎ ‎∴AO⊥平面BCD；‎ ‎（2）结合题意,建立坐标系,以OB为y轴，以OC为x轴，以AO为z轴，则 ‎,‎ 解得 ‎【点睛】‎ 本道题考查了直线与平面垂直判定，考查了空间向量数量积计算公式，难度中等。‎ ‎19．已知圆C的圆心为(1，1)，直线与圆C相切。‎ ‎（1）求圆C的标准方程；‎ ‎（2）若直线过点(2，3)，且被圆C所截得的弦长为2，求直线的方程。‎ ‎【答案】（1）（2）或 ‎【解析】‎ ‎【分析】‎ ‎（1）结合点到直线距离公式，计算半径，建立圆方程，即可。（2）结合点到直线距离公式，计算斜率k，建立直线方程，即可。‎ ‎【详解】‎ ‎（1）该圆心到直线距离为，所以该圆的标准方程为 ‎（2）结合题意，可以计算出该圆心到直线距离，圆心坐标为 该直线过点，可设出该直线方程为，结合点到直线距离公式 则，解得，同时当直线为也满足条件，故直线方程为 ‎【点睛】‎ 本道题考查了点到直线距离公式，关键抓住圆心到直线距离，建立方程，计算，属于中档题。‎ ‎20．已知函数的图象过点，且在点处的切线方程为.‎ ‎（1）求的解析式；‎ ‎（2）求的单调区间.‎ ‎【答案】(1) 解析式为;(2) 在和内是增函数，在内是减函数.‎ ‎【解析】试题分析：‎ ‎(1)由题意结合切线的性质可得关于实数b,c的方程组，求解方程组可得函数的解析式为.‎ ‎(2)结合(1)中函数的解析式求导可得，结合导函数与原函数的单调性之间的关系可得函数的单调递增区间为和，单调递减区间为.‎ 试题解析：‎ ‎（1）由的图象经过点，知，‎ ‎∴， .‎ 由在点处的切线方程为，‎ 知，即， .‎ ‎∴即解得.‎ 故所求的解析式是.‎ ‎（2）‎ 令，得或；‎ 令，得.‎ 故的单调递增区间为和 单调递减区间为.‎ ‎21．在平面直角坐标系xoy中，已知A(1,0)，点B在直线x=－1上，M点满足，，M点的轨迹为曲线C。‎ ‎（1）求曲线C的方程；‎ ‎（2）斜率为的直线l与曲线C交于P、Q两点，曲线C上是否存在定点N，使得NP与NQ的倾斜角互补，若存在，求点N的坐标，若不存在请说明理由。‎ ‎【答案】（1）（2）（1，2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）设出M,B的坐标，结合，建立方程，得出曲线C的方程，即可。（2）设出N的坐标，设出PQ的方程，代入抛物线方程，分别表示，求和，即可。‎ ‎【详解】‎ 解：（1）设M点的坐标为则 则 由于 即 所以曲线C的方程是 ‎（2）假设满足条件的点N存在，设设PQ的方程为 联立消去x得 则的斜率分别为 同理 点N的坐标是（1，2）‎ ‎【点睛】‎ 本道题考查了直线与抛物线位置关系，考查了抛物线方程求解，难度偏难。‎ ‎22．已知函数，，其中.‎ ‎（Ⅰ）讨论的单调性；‎ ‎（Ⅱ）设函数，当时，若，，总有成立，求实数的取值范围。‎ ‎【答案】（1）在上单调递减，上单调递增（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）计算导函数，结合导函数与原函数单调性关系，判定单调性，即可。（2）结合的导函数，结合导函数与原函数单调性，判定最大值，结合题意，建立不等式，计算m的范围，即可。‎ ‎【详解】‎ 解：（1）的定义域为，且 当时，在上单调递增；‎ 当时，由得由得；‎ 故在上单调递减，在上单调递增 ‎（2）当时，，‎ 由得或 当时，；当时，.‎ 所以在上，‎ 而“，，总有成立”等价于 ‎“在上的最大值不小于在上的最大值”‎ 而在上的最大值为 所以有 所以实数的取值范围是 ‎【点睛】‎ 本道题考查了导函数与原函数的单调性关系，考查了利用导函数计算最值，难度偏难。‎