2017-2018学年江苏省扬州中学高二上学期期中数学试题（解析版）

2017-2018学年江苏省扬州中学高二上学期期中数学试题（解析版）

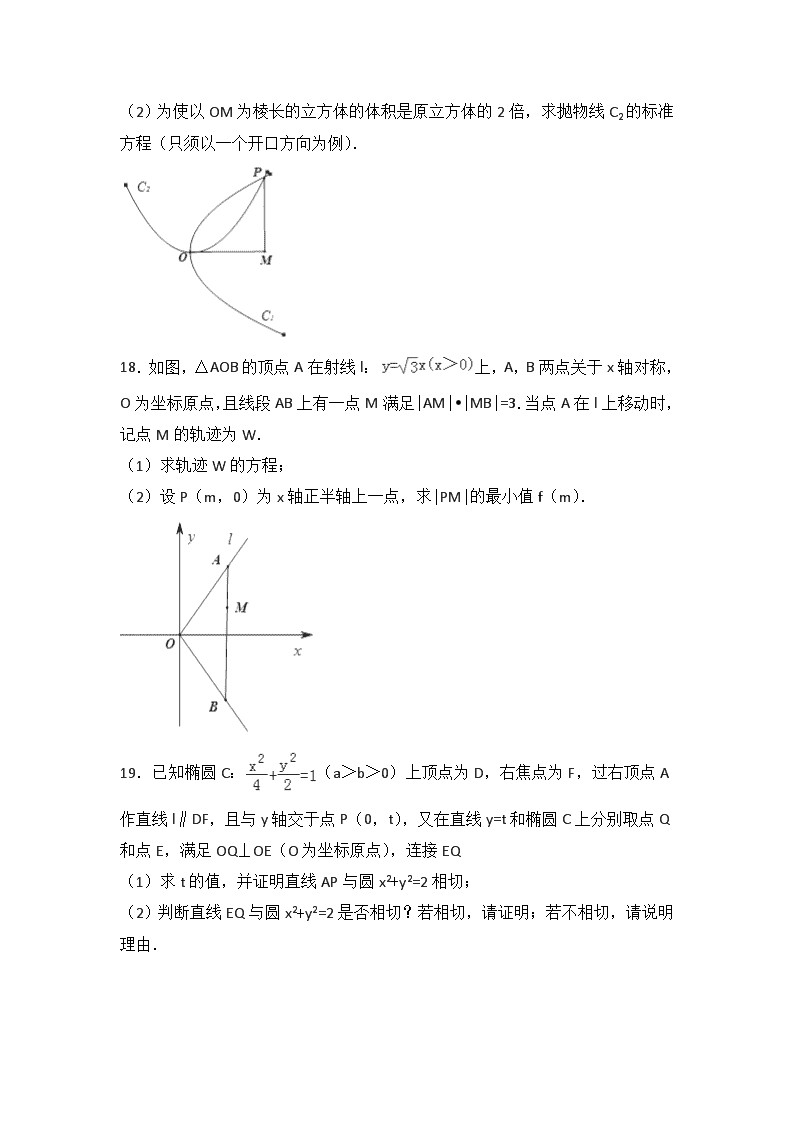
‎2017-2018学年江苏省扬州中学高二（上）期中数学试卷 ‎　‎ 一、填空题：‎ ‎1．（3分）直线l：2x﹣y+1=0的斜率为　 　．‎ ‎2．（3分）命题p：∃x∊R，使得x2+1≤0的否定为　 　．‎ ‎3．（3分）直线l：kx+y﹣2k=0经过定点的坐标为　 　．‎ ‎4．（3分）若命题p：x12+y12＜4（x1，y1∈R），命题q：点（x1，y1）在圆x2+y2=4内，则p是q的　 　条件．‎ ‎5．（3分）已知两条直线l1：x+ay=2a+2，l2：ax+y=a+1，若l1⊥l2，则a=　 　．‎ ‎6．（3分）命题p：“若a＞b，则＜”的否命题是　 　（填：真、假）命题．‎ ‎7．（3分）两圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0的公切线条数为　 　．‎ ‎8．（3分）若直线x﹣y﹣2=0被圆（x﹣a）2+y2=4所截得的弦长为，则实数a的值为　 　．‎ ‎9．（3分）离心率为2且与椭圆+=1有共同焦点的双曲线方程是　 　．‎ ‎10．（3分）椭圆+=1和双曲线﹣y2=1的公共焦点为F1、F2，P是两曲线的一个交点，那么cos∠F1PF2的值是　 　．‎ ‎11．（3分）在平面直角坐标系xOy中，由不等式所确定的图形的面积为　 　．‎ ‎12．（3分）已知点F是椭圆 的右焦点，过原点的直线交椭圆于点A、P，PF垂直于x轴，直线AF交椭圆于点B，PB⊥PA，则该椭圆的离心率e=　 　．‎ ‎13．（3分）在平面直角坐标系xOy中，抛物线y2=2x的焦点为F．设M是抛物线上的动点，则的最大值为　 　．‎ ‎14．（3分）已知对于点A（0，12），B（10，9），C（8，0），D（﹣4，7），存在唯一一个正方形S满足这四个点在S的不同边所在直线上，设正方形S面积为k，则10k的值为　 　．‎ ‎　‎ 二、解答题：‎ ‎15．已知命题p：“方程表示焦点在x轴上的椭圆”，命题q：“方程表示双曲线”．‎ ‎（1）若p是真命题，求实数k的取值范围；‎ ‎（2）若q是真命题，求实数k的取值范围；‎ ‎（3）若“p∨q”是真命题，求实数k的取值范围．‎ ‎16．已知圆M的方程为x2+（y﹣2）2=1，直线l的方程为x﹣2y=0，点P在直线l上，过点P作圆M的切线PA，PB，切点为A，B．‎ ‎（1）若∠APB=60°，试求点P的坐标；‎ ‎（2）若P点的坐标为（2，1），过P作直线与圆M交于C，D两点，当CD=时，求直线CD的方程．‎ ‎17．古希腊有一著名的尺规作图题“倍立方问题”：求作一个立方体，使它的体积等于已知立方体体积的2倍．倍立方问题可以利用抛物线（可尺规作图）来解决．首先作一个通经为2a（其中正数a为原立方体的棱长）的抛物线C1，如图，再作一个顶点与抛物线C1顶点O重合而对称轴垂直的抛物线C2，且与C1交于不同于点O的一点P，自点P向抛物线C1的对称轴作垂线，垂足为M，可使以OM为棱长的立方体的体积为原立方体的2倍．‎ ‎（1）建立适当的平面直角坐标系，求抛物线C1的标准方程；‎ ‎（2）为使以OM为棱长的立方体的体积是原立方体的2倍，求抛物线C2的标准方程（只须以一个开口方向为例）．‎ ‎18．如图，△AOB的顶点A在射线l：上，A，B两点关于x轴对称，O为坐标原点，且线段AB上有一点M满足|AM|•|MB|=3．当点A在l上移动时，记点M的轨迹为W．‎ ‎（1）求轨迹W的方程；‎ ‎（2）设P（m，0）为x轴正半轴上一点，求|PM|的最小值f（m）．‎ ‎19．已知椭圆C：（a＞b＞0）上顶点为D，右焦点为F，过右顶点A作直线l∥DF，且与y轴交于点P（0，t），又在直线y=t和椭圆C上分别取点Q和点E，满足OQ⊥OE（O为坐标原点），连接EQ ‎（1）求t的值，并证明直线AP与圆x2+y2=2相切；‎ ‎（2）判断直线EQ与圆x2+y2=2是否相切？若相切，请证明；若不相切，请说明理由．‎ ‎20．已知椭圆C：左焦点F，左顶点A，椭圆上一点B满足BF⊥x轴，且点B在x轴下方，BA连线与左准线l交于点P，过点P任意引一直线与椭圆交于C、D，连结AD、BC交于点Q，若实数λ1，λ2满足：=λ1，=λ2．‎ ‎（1）求λ1•λ2的值；‎ ‎（2）求证：点Q在一定直线上．‎ ‎　‎ ‎2017-2018学年江苏省扬州中学高二（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、填空题：‎ ‎1．（3分）直线l：2x﹣y+1=0的斜率为　2　．‎ ‎【分析】根据题意，将直线的方程变形为y=2x+1，由直线斜截式的形式分析可得答案．‎ ‎【解答】解：根据题意，直线l：2x﹣y+1=0，变形可得y=2x+1，‎ 其斜率k=2；‎ 故答案为：2．‎ ‎【点评】本题考查直线的斜率，注意将直线的方程变形为斜截式方程．‎ ‎　‎ ‎2．（3分）命题p：∃x∊R，使得x2+1≤0的否定为　∀x∈R，都有x2+1＞0　．‎ ‎【分析】直接利用特称命题的否定是全称命题，写出经过即可．‎ ‎【解答】解：因为特称命题的否定是全称命题，所以，命题p：∃x∊R，使得x2+1≤0”的否定为：∀x∈R，都有x2+1＞0．‎ 故答案为：∀x∈R，都有x2+1＞0．‎ ‎【点评】本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．‎ ‎　‎ ‎3．（3分）直线l：kx+y﹣2k=0经过定点的坐标为　（2，0）　．‎ ‎【分析】直线l：kx+y﹣2k=0化为：k（x﹣2）+y=0，令，解出即可得出．‎ ‎【解答】解：直线l：kx+y﹣2k=0化为：k（x﹣2）+y=0，令，解得x=2，y=0．‎ 因此直线经过定点的坐标为（2，0）．‎ 故答案为：（2，0）．‎ ‎【点评】本题考查了直线系的应用，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎4．（3分）若命题p：x12+y12＜4（x1，y1∈R），命题q：点（x1，y1）在圆x2+y2=4内，则p是q的　充要　条件．‎ ‎【分析】命题q：点（x1，y1）在圆x2+y2=4内⇔x12+y12＜4（x1，y1∈R），即可判断出结论．‎ ‎【解答】解：命题q：点（x1，y1）在圆x2+y2=4内⇔x12+y12＜4（x1，y1∈R），‎ ‎∴p是q的充要条件．‎ 故答案为：充要．‎ ‎【点评】本题考查了点与圆的位置关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎5．（3分）已知两条直线l1：x+ay=2a+2，l2：ax+y=a+1，若l1⊥l2，则a=　0　．‎ ‎【分析】对a分类讨论，利用两条直线相互垂直与斜率的关系即可得出．‎ ‎【解答】解：a=0时，两条直线方程分别化为：x=2；y=1，此时两条直线相互垂直．‎ a≠0时，由﹣×（﹣a）=1≠﹣1，可知两条直线不垂直．‎ 综上可得：a=0．‎ 故答案为：0．‎ ‎【点评】本题考查了两条直线相互垂直与斜率的关系、分类讨论方法，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎6．（3分）命题p：“若a＞b，则＜”的否命题是　假　（填：真、假）命题．‎ ‎【分析】写出命题p的否命题，再判断它的真假性．‎ ‎【解答】解：命题p：“若a＞b，则＜”的否命题是 ‎“若a≤b，则≥”，它是假命题；‎ 例如a=﹣1，b=1时，有＜．‎ 故答案为：假．‎ ‎【点评】本题考查了命题与它的否命题的应用问题，是基础题．‎ ‎　‎ ‎7．（3分）两圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0的公切线条数为　2　．‎ ‎【分析】求圆x2+y2﹣6x+16y﹣48=0和圆x2+y2+4x﹣8y﹣44=0的圆心、半径及两圆的圆心距，得到圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0相交，由此能求出圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0的公切线条数．‎ ‎【解答】解：圆x2+y2﹣6x+16y﹣48=0的圆心C1（3，﹣8），半径r1==11．‎ 圆x2+y2+4x﹣8y﹣44=0的圆心C2（﹣2，4），半径r2==8，‎ ‎|C1C2|==13，‎ ‎∵|r1﹣r2|=3＜|C1C2|=13＜r1+r2，‎ ‎∴圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0相交，‎ ‎∴圆x2+y2﹣6x+16y﹣48=0与x2+y2+4x﹣8y﹣44=0的公切线条数为2条．‎ 故答案为：2．‎ ‎【点评】本题考查两圆的公切线的条数的求法，考查圆、两点间距离公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．‎ ‎　‎ ‎8．（3分）若直线x﹣y﹣2=0被圆（x﹣a）2+y2=4所截得的弦长为，则实数a的值为　0或4　．‎ ‎【分析】由圆的方程，得到圆心与半径，再求得圆心到直线的距离，由 求解．‎ ‎【解答】解：∵圆（x﹣a）2+y2=4‎ ‎∴圆心为：（a，0），半径为：2‎ 圆心到直线的距离为：‎ ‎∵，‎ 即，‎ ‎∴a=4，或a=0．‎ 故答案为：0或4．‎ ‎【点评】本题考查直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，得到，这是解题的关键．‎ ‎　‎ ‎9．（3分）离心率为2且与椭圆+=1有共同焦点的双曲线方程是　﹣=1　．‎ ‎【分析】根据题意，求出椭圆的焦点，分析可得双曲线的焦点在x轴上，且c=4，可设双曲线的方程为﹣=1，由离心率公式和c的值可得a的值，进而计算可得b的值，将a、b的值代入双曲线的方程，即可得答案．‎ ‎【解答】解：根据题意，椭圆+=1的焦点为（±4，0），‎ 又由双曲线与椭圆有共同焦点，则双曲线的焦点在x轴上，且c=4，‎ 设其方程为﹣=1，‎ 又由双曲线的离心率e=2，即e==2，则a=2，‎ b2=c2﹣a2=16﹣4=12，‎ 则双曲线的方程为：﹣=1；‎ 故答案为：﹣=1．‎ ‎【点评】本题考查双曲线的几何性质，注意先求出椭圆的焦点，方便设出双曲线的方程．‎ ‎　‎ ‎10．（3分）椭圆+=1和双曲线﹣y2=1的公共焦点为F1、F2，P是两曲线的一个交点，那么cos∠F1PF2的值是　　．‎ ‎【分析】先求出公共焦点分别为F1，F2，再联立方程组求出P，由此可以求出 ，最后根据公式cos∠F1PF2=进行求解即可．‎ ‎【解答】解：由题意知F1（﹣2，0），F2（2，0），‎ 解方程组 得 ，‎ 取P点坐标为（ ），，‎ cos∠F1PF2==‎ 故答案为：．‎ ‎【点评】本题考查圆锥曲线的性质和应用，解题时要注意公式的灵活运用，属基础题．‎ ‎　‎ ‎11．（3分）在平面直角坐标系xOy中，由不等式 所确定的图形的面积为　50π　．‎ ‎【分析】根据题意，将x2+x﹣2≥y2+y﹣2变形可得或，又由x2+y2≤100表示以原点为圆心，10为半径的圆以及圆的内部，即可作出不等式组表示的图形，分析可得其面积为圆O面积的一半，计算即可得答案．‎ ‎【解答】解：根据题意，‎ 若x2+x﹣2≥y2+y﹣2，变形可得x2﹣y2≥y﹣2﹣x﹣2，‎ 即x2﹣y2≥，‎ 分析可得：或，‎ 又由x2+y2≤100表示以原点为圆心，10为半径的圆以及圆的内部，‎ 则不等式所确定的图形如图：‎ 其面积为圆O面积的一半，即不等式组所确定的图形的面积为×102×π=50π；‎ 故答案为：50π．‎ ‎【点评】本题考查二元二次不等式组的应用，关键是分析不等式组表示的平面区域．‎ ‎　‎ ‎12．（3分）已知点F是椭圆 的右焦点，过原点的直线交椭圆于点A、P，PF垂直于x轴，直线AF交椭圆于点B，PB⊥PA，则该椭圆的离心率e=　　．‎ ‎【分析】由题意得该椭圆的形状确定，与大小无关．因此设a=1，得P（c，b2），从而A（﹣c，﹣b2），可得到直线AF的方程为：y=（x﹣c），与椭圆方程联解得出点B（，），由此得出PB的斜率k1，并化简得k1=﹣2c，结合PA的斜率k2=且PB⊥PA，由k1k2=﹣1列式并解之，可得b=c=，最终得出该椭圆的离心率e．‎ ‎【解答】解：根据题意椭圆的离心率为定值，故椭圆的形状确定，与大小无关 因此设a=1，得椭圆的方程为，‎ 求出椭圆的半焦距c，即得椭圆的离心率．‎ 由F（c，0）及PF⊥x轴，得P（c，b2）‎ ‎∵PA的中点为坐标原点O ‎∴A的坐标为（﹣c，﹣b2），得直线AF的斜率k==‎ ‎∴直线AF的方程为：y=（x﹣c）‎ 由联解，得B的横坐标xB=，‎ 将b2=1﹣c2代入，化简得xB=，代入直线AF方程，得B的纵坐标yB=‎ ‎∴直线PB的斜率k1==﹣2c ‎∵PA的斜率k2=，且PB⊥PA，‎ ‎∴k1k2=﹣1，得﹣2c•=﹣1，解之得b=c=‎ 因此，该椭圆的离心率e==‎ 故答案为：‎ ‎【点评】本题给出满足特殊条件的椭圆，求该椭圆的离心率，着重考查了椭圆的标准方程和简单几何性质等知识，属于中档题．‎ ‎　‎ ‎13．（3分）在平面直角坐标系xOy中，抛物线y2=2x的焦点为F．设M是抛物线上的动点，则的最大值为　　．‎ ‎【分析】设M（m，n）到抛物线y2=2x的准线x=﹣的距离等于d，由抛物线的定义可得=，化简为，令m﹣=t，利用基本不等式可求得最大值．‎ ‎【解答】解：焦点F（，0），设M（m，n），则n2=2m，m＞0，设M到准线x=﹣的距离等于d，‎ 则由抛物线的定义得====，‎ 令m﹣=t，‎ 依题意知，m＞0，‎ 若t＞0，‎ 则==≤=，‎ ‎∴tmax=，此时==；‎ 若﹣＜t＜0，y=t++单调递减，故y＜﹣﹣+=﹣1，∈（﹣1，0）；‎ 综上所述，=．‎ 故答案为：．‎ ‎【点评】本题考查抛物线的定义、简单性质，基本不等式的应用，体现了换元的思想，把化为 是解题的关键和难点，属于难题．‎ ‎　‎ ‎14．（3分）已知对于点A（0，12），B（10，9），C（8，0），D（﹣4，7），存在唯一一个正方形S满足这四个点在S的不同边所在直线上，设正方形S面积为k，则10k的值为　1936　．‎ ‎【分析】设m为过点B的正方形S的边所在直线的斜率，则该直线方程l1：mx﹣y+（9﹣10m）=0，过点C的正方形S的边所在直线方程l2：x+my﹣8=0，点D到l1的距离等于点A到l1的距离，由此能求出10k．‎ ‎【解答】解：点A（0，12），B（10，9），C（8，0），D（﹣4，7），‎ 设m为过点B的正方形S的边所在直线的斜率，‎ 则该直线方程l1：y﹣9=m（x﹣10），即mx﹣y+（9﹣10m）=0，‎ 过点C的正方形S的边所在直线方程l2：x+my﹣8=0，‎ ‎∵点D到l1的距离等于点A到l1的距离，‎ ‎∴=，‎ 解得m=或m=﹣3，‎ 当m=时，点A与点C在l1的两侧，矛盾，‎ 当m=3时，符合，此时k=（）2=，‎ ‎∴10k=1936．‎ 故答案为：1936．‎ ‎【点评】本题考查实数值的求法，考查直线方程、点到直线的距离公式等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．‎ ‎　‎ 二、解答题：‎ ‎15．已知命题p：“方程表示焦点在x轴上的椭圆”，命题q：“方程表示双曲线”．‎ ‎（1）若p是真命题，求实数k的取值范围；‎ ‎（2）若q是真命题，求实数k的取值范围；‎ ‎（3）若“p∨q”是真命题，求实数k的取值范围．‎ ‎【分析】（1）p是真命题，则9﹣k＞k﹣1＞0；（2）q是真命题，则（2﹣k）k＜0；（3）若“p∨q”是真命题，则p、q至少一个是真命题，分类讨论即可．‎ ‎【解答】解：（1）p：“方程表示焦点在x轴上的椭圆”，是真命题，则9﹣k＞k﹣1＞0，∴1＜k＜5；‎ ‎（2）q：“方程表示双曲线”是真命题，则（2﹣k）k＜0，∴k＜0或k＞2‎ ‎（3）若“p∨q”是真命题，则p、q至少一个是真命题，即一真一假或全为真 ‎∴或或 ‎∴1＜k≤2或k＜0或k≥5或2＜k＜5‎ ‎∴k＜0或k＞1．‎ ‎【点评】本题考查命题真假的运用，考查解不等式，考查分类讨论的数学思想，属于中档题．‎ ‎　‎ ‎16．已知圆M的方程为x2+（y﹣2）2=1，直线l的方程为x﹣2y=0，点P在直线l上，过点P作圆M的切线PA，PB，切点为A，B．‎ ‎（1）若∠APB=60°，试求点P的坐标；‎ ‎（2）若P点的坐标为（2，1），过P作直线与圆M交于C，D两点，当CD=时，求直线CD的方程．‎ ‎【分析】（1）设P（2m，m），代入圆方程，解得m，进而可知点P的坐标．‎ ‎（2）设直线CD的斜率为k，由P的坐标表示出直线CD的解析式，利用垂径定理及勾股定理求出圆心到直线CD的距离d，利用点到直线的距离公式列出关于k的方程，求出方程的解得到k的值，即可求出直线CD的方程．‎ ‎【解答】解：（1）设P（2m，m），由题可知：MP==2，即（2m）2+（m﹣2）2=4，‎ 解得：m=0或m=，‎ 则P的坐标为（0，0）或（，）；‎ ‎（2）设直线CD的斜率为k，由P（2，1），得到直线CD的解析式为y﹣1=k（x﹣2），即kx﹣y+1﹣2k=0，‎ ‎∵圆的半径r=1，CD=，‎ ‎∴圆心到直线CD的距离d==，即=，‎ 解得：k=﹣或k=﹣1，‎ 则直线CD的解析式为x+7y﹣9=0或x+y﹣3=0．‎ ‎【点评】此题考查了直线与圆的位置关系，涉及的知识有：锐角三角函数定义，两点间的距离公式，点到直线的距离公式，垂径定理，勾股定理，以及直线的点斜式方程，是一道综合性较强的试题．‎ ‎　‎ ‎17．古希腊有一著名的尺规作图题“倍立方问题”：求作一个立方体，使它的体积等于已知立方体体积的2倍．倍立方问题可以利用抛物线（可尺规作图）来解决．首先作一个通经为2a（其中正数a为原立方体的棱长）的抛物线C1，如图，再作一个顶点与抛物线C1顶点O重合而对称轴垂直的抛物线C2，且与C1交于不同于点O的一点P，自点P向抛物线C1的对称轴作垂线，垂足为M，可使以OM为棱长的立方体的体积为原立方体的2倍．‎ ‎（1）建立适当的平面直角坐标系，求抛物线C1的标准方程；‎ ‎（2）为使以OM为棱长的立方体的体积是原立方体的2倍，求抛物线C2的标准方程（只须以一个开口方向为例）．‎ ‎【分析】（1）以O为原点，OM为x轴正向建立平面直角坐标系，由抛物线C1的通经为2a，可得标准方程为y2=2ax．‎ ‎（2）设抛物线C2：x2=my（m＞0），联立抛物线C1、C2得：x4=2am2x，解得x=0或x3=2am2‎ 由题意OM3=x3=2am2=2a3．可得，m=a，即可．‎ ‎【解答】解（1）以O为原点，OM为x轴正向建立平面直角坐标系，‎ 由题意，抛物线C1的通经为2a，所以标准方程为y2=2ax．‎ ‎（2）：设抛物线C2：x2=my（m＞0），联立抛物线C1、C2得：x4=2am2x，解得x=0或x3=2am2‎ 由题意OM3=x3=2am2=2a3．‎ 所以，m=a，‎ 所以抛物线C2为：x2=ay．‎ ‎【点评】本题考查了抛物线的方程，考查了转化思想，属于中档题．‎ ‎　‎ ‎18．如图，△AOB的顶点A在射线l：上，A，B两点关于x轴对称，O为坐标原点，且线段AB上有一点M满足|AM|•|MB|=3．当点A在l上移动时，记点M的轨迹为W．‎ ‎（1）求轨迹W的方程；‎ ‎（2）设P（m，0）为x轴正半轴上一点，求|PM|的最小值f（m）．‎ ‎【分析】（1）由A，B两点关于x轴对称，得到AB边所在直线与y轴平行．设M（x，y），由题意得出x，y之间的关系，整理可得点M的轨迹W的方程；‎ ‎（2）P（m，0）为x轴正半轴上一点，当0＜m≤1时，|PM|min=1﹣m；当m＞1时，利用两点间的距离公式写出|PM|，配方后对m分类求最值．‎ ‎【解答】解：（1）∵A，B两点关于x轴对称，‎ ‎∴AB边所在直线与y轴平行．‎ 设M（x，y），由题意，得A（x，x），B（x，﹣x），‎ ‎∴|AM|=x﹣y，|MB|=y+x ‎∵|AM|•|MB|=3，‎ ‎∴（x﹣y）（y+x）=3，即x2﹣=1，‎ ‎∴点M的轨迹W的方程为x2﹣=1，x≥1；‎ ‎（2）P（m，0）为x轴正半轴上一点，‎ 当0＜m≤1时，|PM|min=1﹣m；‎ 当m＞1时，则|PM|==‎ ‎==．‎ 若，即m≤4，则当x=1时，|PM|min=m﹣1；‎ 若，即m＞4，则当x=时，|PM|的最小值f（m）=．‎ 综上，f（m）=．‎ ‎【点评】本题主要考查直线与圆锥曲线的综合问题、轨迹方程、双曲线方程等基础知识，考查运算求解能力、转化思想，训练了分类讨论求二次函数的最值．属于中档题．‎ ‎　‎ ‎19．已知椭圆C：（a＞b＞0）上顶点为D，右焦点为F，过右顶点A作直线l∥DF，且与y轴交于点P（0，t），又在直线y=t和椭圆C上分别取点Q和点E，满足OQ⊥OE（O为坐标原点），连接EQ ‎（1）求t的值，并证明直线AP与圆x2+y2=2相切；‎ ‎（2）判断直线EQ与圆x2+y2=2是否相切？若相切，请证明；若不相切，请说明理由．‎ ‎【分析】（1）由线l∥DF，可得kAP=kDF，即，解得t=2．由圆x2+y2=2的圆心（0，0）到直线AP 的距离证明相切．‎ ‎（2）设Q（m，2），E（x0，y0）．设O到直线QE的距离为d，由，得，由△QPE的面积可得：OQ2•OE2=QE2•d2，‎ ‎（m2+4）（）=[]•d2⇒=•d2=，⇒d2=2，d=，即可判定．‎ ‎【解答】解：（1）可得A（2，0），D（0，），F（，0），‎ ‎∵线l∥DF，∴kAP=kDF，即，解得t=2．‎ ‎∴直线AP：x+y﹣2=0‎ 圆x2+y2=2的圆心（0，0）到直线AP 的距离为 而圆x2+y2=2的半径为，∴直线AP与圆x2+y2=2相切；‎ ‎（2）设Q（m，2），E（x0，y0）．设O到直线QE的距离为d，‎ 则有OQ2=m2+4，OE2=，kOE=﹣，‎ 由，得，‎ 由△QPE的面积可得：OQ2•OE2=QE2•d2，‎ ‎（m2+4）（）=[]•d2…①‎ 又∵4y0=﹣2mx0，，，‎ ‎∴①化简为（m2+4）•=（）•d2‎ ‎⇒=•d2=，‎ ‎⇒d2=2，d=，‎ ‎∴直线EQ与圆x2+y2=2相切．‎ ‎【点评】本题考查了椭圆方程，圆与直线的位置关系，属于中档题．‎ ‎　‎ ‎20．已知椭圆C：左焦点F，左顶点A，椭圆上一点B满足BF⊥x轴，且点B在x轴下方，BA连线与左准线l交于点P，过点P任意引一直线与椭圆交于C、D，连结AD、BC交于点Q，若实数λ1，λ2满足：=λ1，=λ2．‎ ‎（1）求λ1•λ2的值；‎ ‎（2）求证：点Q在一定直线上．‎ ‎【分析】（1）由椭圆方程求得F坐标，结合BF⊥x轴，不妨设B（﹣2，﹣3），结合A（﹣4，0），求得直线AB方程，进一步求得P的坐标，由=λ1，得 ‎，再由=λ2，得，再由，可得，利用，由系数相等即可求得；‎ ‎（2）设点C（x1，y1），D（x2，y2），Q（x0，y0），由=λ1，得，，代入椭圆方程：，求得λ1，同理求得λ2，代入，可得x0+y0+2=0，说明点Q在定直线x﹣y+2=0上．‎ ‎【解答】解：（1）由椭圆C：，得a2=16，b2=12，‎ ‎∴，则F（﹣2，0），‎ 由BF⊥x轴，不妨设B（﹣2，﹣3），∵A（﹣4，0），‎ ‎∴直线AB：y=﹣（x+4），‎ 又左准线l：x=﹣8，∴P（﹣8，6），‎ 又=λ1，∴，得，‎ 由=λ2，得，得，‎ 又，∴，‎ ‎∵，由系数相等得，‎ 得；‎ ‎（2）证明：设点C（x1，y1），D（x2，y2），Q（x0，y0），‎ 由=λ1，得（x1+2，y1+3）=λ1（x0﹣x1，y0﹣y1），‎ 得，，‎ 代入椭圆方程：，得：，‎ 显然λ1≠0，∴，‎ 同理得：，‎ 又由（1），‎ ‎∴，‎ 整理得：x0+y0+2=0，‎ 即点Q在定直线x﹣y+2=0上．‎ ‎【点评】本题考查椭圆的简单性质，考查平面向量在求解圆锥曲线问题中的应用，考查计算能力，属难题．‎ ‎　‎