2017-2018学年重庆市彭水一中高二上学期期中数学试题（文科）（解析版）

2017-2018学年重庆市彭水一中高二上学期期中数学试题（文科）（解析版）

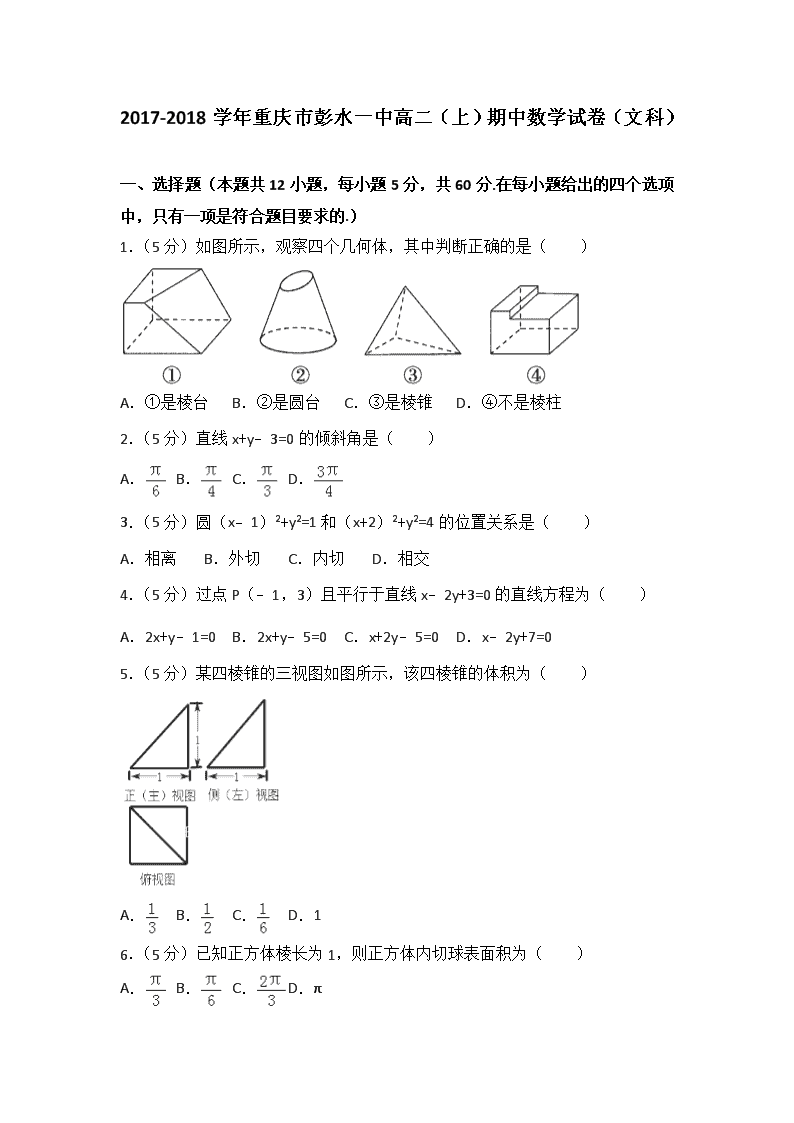
‎2017-2018学年重庆市彭水一中高二（上）期中数学试卷（文科）‎ ‎　‎ 一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．（5分）如图所示，观察四个几何体，其中判断正确的是（　　）‎ A．①是棱台 B．②是圆台 C．③是棱锥 D．④不是棱柱 ‎2．（5分）直线x+y﹣3=0的倾斜角是（　　）‎ A． B． C． D．‎ ‎3．（5分）圆（x﹣1）2+y2=1和（x+2）2+y2=4的位置关系是（　　）‎ A．相离 B．外切 C．内切 D．相交 ‎4．（5分）过点P（﹣1，3）且平行于直线x﹣2y+3=0的直线方程为（　　）‎ A．2x+y﹣1=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+7=0‎ ‎5．（5分）某四棱锥的三视图如图所示，该四棱锥的体积为（　　）‎ A． B． C． D．1‎ ‎6．（5分）已知正方体棱长为1，则正方体内切球表面积为（　　）‎ A． B． C． D．π ‎7．（5分）方程x2+y2+2kx+4y+3k+8=0表示一个圆，则实数k的取值范围是（　　）‎ A． B． C．﹣1＜k＜1 D．k＜﹣1或k＞4‎ ‎8．（5分）关于直线l，m及平面α，β，下列命题中正确的是（　　）‎ A．若l⊥α，l∥β，则α⊥β B．若l∥α，m∥α，则l∥m C．若l∥α，l⊥m，则m⊥α D．若l∥α，α∩β=m，则l∥m ‎9．（5分）直线3x﹣4y﹣4=0被圆（x﹣3）2+y2=9截得的弦长为（　　）‎ A． B．4 C． D．2‎ ‎10．（5分）已知两个平面垂直，下列命题 ‎①一个平面内的已知直线必垂直于另一个平面的任意一条直线；‎ ‎②一个平面内的已知直线必垂直于另一个平面的无数条直线；‎ ‎③一个平面内的任一条直线必垂直于另一个平面；‎ ‎④过一个平面内任意一点作交线的垂线，则垂线必垂直于另一个平面．‎ 其中正确的个数是（　　）‎ A．3 B．2 C．1 D．0‎ ‎11．（5分）点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，则点O是△ABC的（　　）‎ A．垂心 B．重心 C．内心 D．外心 ‎12．（5分）若直线y=kx+4+2k与曲线有两个交点，则k的取值范围是（　　）‎ A．[1，+∞） B．[﹣1，﹣） C．（，1] D．（﹣∞，﹣1]‎ ‎　‎ 二、填空题（本题共4小题，每小题5分，共20分.）‎ ‎13．（5分）点A（2，1）到直线x﹣y+1=0的距离为　 　．‎ ‎14．（5分）已知直线过点（1，1），且在两个坐标轴上的截距相等，则该直线的方程为　 　．‎ ‎15．（5分）若正三棱柱的所有棱长均为a，且其体积为16，则a=　 　．‎ ‎16．（5分）若圆x2+y2=r2（r＞0）上恰有相异的两点到直线4x﹣3y+‎ ‎25=0的距离等于，则r的取值范围是　 　．‎ ‎　‎ 三、解答题：（共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（12分）三角形的三个顶点为A（4，0），B（6，5），C（0，3）．‎ ‎（1）求BC边上高所在直线的方程；‎ ‎（2）求BC边上中线所在直线的方程．‎ ‎18．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥面ABCD，E、F分别为PB、PD的中点，‎ ‎（1）求证：EF∥面ABCD；‎ ‎（2）求证：BD⊥面PAC．‎ ‎19．（12分）（1）已知△AOB的顶点坐标分别是A（4，0），B（0，4），O（0，0），求△AOB外接圆的方程；‎ ‎（2）已知圆C的半径为2，圆心在x轴的正半轴上，直线3x+4y+4=0与圆C相切，求圆C的方程为．‎ ‎20．（12分）已知平行四边形ABCD中，AB=2，E为AB的中点，且△ADE是等边三角形，沿DE把△ADE折起至A1DE的位置，使得A1C=2．‎ ‎（1）F是线段A1C的中点，求证：BF∥平面A1DE；‎ ‎（2）求证：A1D⊥CE；‎ ‎（3）求点A1到平面BCDE的距离．‎ ‎21．（12分）已知过点A（0，﹣1）且斜率为k的直线l与圆C：（x﹣2）2+（y﹣3）2=4交于M，N两点．‎ ‎（1）求k的取值范围；‎ ‎（2）若，其中O为坐标原点，求MN的长度．‎ ‎22．（10分）已知直线l：kx﹣y+2k+1=0，k∈R．‎ ‎（1）当k变化时，直线l恒过一定点P，求点P的坐标；‎ ‎（2）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值．‎ ‎　‎ ‎2017-2018学年重庆市彭水一中高二（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．（5分）如图所示，观察四个几何体，其中判断正确的是（　　）‎ A．①是棱台 B．②是圆台 C．③是棱锥 D．④不是棱柱 ‎【分析】利用几何体的结构特征进行分析判断，能够求出结果．‎ ‎【解答】解：图①不是由棱锥截来的，所以①不是棱台；‎ 图②上、下两个面不平行，所以②不是圆台；‎ 图③是棱锥．‎ 图④前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以④是棱柱．‎ 故选C．‎ ‎【点评】本题考查几何体的结构特征，解题时要认真审题，注意熟练掌握基本概念．‎ ‎　‎ ‎2．（5分）直线x+y﹣3=0的倾斜角是（　　）‎ A． B． C． D．‎ ‎【分析】先求出直线的斜率，再求直线的倾斜角．‎ ‎【解答】解：∵直线x+y﹣3=0斜率k=﹣1，‎ ‎∴直线x+y﹣3=0的倾斜角是为．‎ 故选：D．‎ ‎【点评】本题考查直线的倾斜角的求法，是基础题，解题时要注意直线方程的性质的合理运用．‎ ‎　‎ ‎3．（5分）圆（x﹣1）2+y2=1和（x+2）2+y2=4的位置关系是（　　）‎ A．相离 B．外切 C．内切 D．相交 ‎【分析】求出两个圆的圆心和半径，根据圆圆之间的位置关系的条件即可得到结论 ‎【解答】解：圆O1：（x﹣1）2+y2=1，圆心为O1（1，0），半径为R=1，‎ 圆O2：（x+2）2+y2=4，圆心为O2（﹣2，0），半径为r=2，‎ 则|O1O2|=3，R+r=2+1=3，‎ 故圆O1和圆O2的位置关系是外切，‎ 故选：B ‎【点评】本题主要考查圆与圆的位置关系的判断，求出圆的圆心和半径是解决本题的关键 ‎　‎ ‎4．（5分）过点P（﹣1，3）且平行于直线x﹣2y+3=0的直线方程为（　　）‎ A．2x+y﹣1=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+7=0‎ ‎【分析】设要求的直线的方程为x﹣2y+m=0，再根据所求的直线过点P（﹣1，3），求得m的值，可得结论．‎ ‎【解答】解：设平行于直线x﹣2y+3=0的直线方程为x﹣2y+m=0，再根据所求的直线过点P（﹣1，3），‎ 可得﹣1﹣6+m=0，求得m=7，故要求的直线的方程为 x﹣2y+7=0，‎ 故选：D．‎ ‎【点评】本题主要考查用待定系数法求直线的方程，属于基础题．‎ ‎　‎ ‎5．（5分）某四棱锥的三视图如图所示，该四棱锥的体积为（　　）‎ A． B． C． D．1‎ ‎【分析】由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，代入锥体体积公式，可得答案．‎ ‎【解答】解：由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，‎ 底面面积S=1×1=1，‎ 高h=1，‎ 故体积V==，‎ 故选：A ‎【点评】本题考查的知识点是由三视图求体积和表面积，难度中档．‎ ‎　‎ ‎6．（5分）已知正方体棱长为1，则正方体内切球表面积为（　　）‎ A． B． C． D．π ‎【分析】由正方体棱长为1，得到正方体内切球半径r=，由此能求出正方体内切球表面积．‎ ‎【解答】解：∵正方体棱长为1，‎ ‎∴正方体内切球半径r=，‎ ‎∴正方体内切球表面积为S=4πr2=4π×=π．‎ 故选：D．‎ ‎【点评】‎ 本题考查正方体内切球表面积的求法，考查正方体及其内切球等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．‎ ‎　‎ ‎7．（5分）方程x2+y2+2kx+4y+3k+8=0表示一个圆，则实数k的取值范围是（　　）‎ A． B． C．﹣1＜k＜1 D．k＜﹣1或k＞4‎ ‎【分析】把已知方程配方，由方程表示一个圆得到k2﹣3k﹣4大于0，列出关于k的不等式，求出解集即可得到k的取值范围．‎ ‎【解答】解：把方程配方得：（x+k）2+（y+2）2=k2﹣3k﹣4，因为方程表示一个圆，‎ 则k2﹣3k﹣4＞0，即（k﹣4）（k+1）＞0可化为或，‎ 解得k＞4或k＜﹣1‎ 故选D．‎ ‎【点评】考查学生会把圆的一般方程化为圆的标准方程，掌握方程为圆时的条件，会求一元二次不等式的解集，是一道综合题．‎ ‎　‎ ‎8．（5分）关于直线l，m及平面α，β，下列命题中正确的是（　　）‎ A．若l⊥α，l∥β，则α⊥β B．若l∥α，m∥α，则l∥m C．若l∥α，l⊥m，则m⊥α D．若l∥α，α∩β=m，则l∥m ‎【分析】根据空间线面位置关系的定义，性质进行判断．‎ ‎【解答】解：对于A，∵l∥β，∴存在直线n⊂β，使得l∥n，‎ ‎∵l⊥α，∴n⊥α，又n⊂β，∴α⊥β．故A正确；‎ 对于B，若l∥α，m∥α，则l与m可能平行，相交或异面，故B错误；‎ 对于C，若l∥α，l⊥m，则m与α可能平行也可能相交，故C错误；‎ 对于D，设γ∥α，l⊂γ，则l∥m或l与m为异面直线，故D错误．‎ 故选A．‎ ‎【点评】本题考查了空间线面位置关系的判断，属于中档题．‎ ‎　‎ ‎9．（5分）直线3x﹣4y﹣4=0被圆（x﹣3）2+y2=9截得的弦长为（　　）‎ A． B．4 C． D．2‎ ‎【分析】先根据圆的方程求得圆的圆心坐标和半径，进而利用点到直线的距离求得圆心到直线的距离，进而利用勾股定理求得被截的弦的一半，则弦长可求．‎ ‎【解答】解：根据圆的方程可得圆心为（3，0），半径为3‎ 则圆心到直线的距离为=1‎ ‎∴弦长为2×=4‎ 故选C ‎【点评】本题主要考查了直线与圆相交的性质．解题的关键是利用数形结合的思想，通过半径和弦构成的三角形和圆心到弦的垂线段，利用勾股定理求得答案．‎ ‎　‎ ‎10．（5分）已知两个平面垂直，下列命题 ‎①一个平面内的已知直线必垂直于另一个平面的任意一条直线；‎ ‎②一个平面内的已知直线必垂直于另一个平面的无数条直线；‎ ‎③一个平面内的任一条直线必垂直于另一个平面；‎ ‎④过一个平面内任意一点作交线的垂线，则垂线必垂直于另一个平面．‎ 其中正确的个数是（　　）‎ A．3 B．2 C．1 D．0‎ ‎【分析】为了对各个选项进行甄别，不必每个选项分别构造一个图形，只须考查正方体中互相垂直的两个平面：A1ABB1，ABCD即可．‎ ‎【解答】解：考察正方体中互相垂直的两个平面：A1ABB1，ABCD．‎ 对于①：一个平面内的已知直线不一定垂直于另一个平面的任意一条直线；如图中A1B与AB不垂直；‎ 对于②：一个平面内的已知直线必垂直于另一个平面的无数条直线；这一定是正确的，如图中，已知直线A1B，在平面ABCD中，所有与BC平行直线都与它垂直；‎ 对于③：一个平面内的任一条直线不一定垂直于另一个平面；如图中：A1B；‎ 对于④：过一个平面内任意一点作交线的垂线，则垂线不一定垂直于另一个平面，如图中A1D，它垂直于AB，但不垂直于平面ABCD．‎ 故选C．‎ ‎【点评】本题主要考查了平面与平面垂直的性质，线面垂直的选择题可以在一个正方体模型中甄别，而不必每个选项分别构造一个图形，广东卷07文6、08文7理5、09文6理5等莫不如此．‎ ‎　‎ ‎11．（5分）点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，则点O是△ABC的（　　）‎ A．垂心 B．重心 C．内心 D．外心 ‎【分析】点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，可证得△POA≌△POB≌△POC，从而证得OA=OB=OC，符合这一性质的点O是△ABC外心．‎ ‎【解答】证明：点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，‎ 故△POA，△POB，△POC都是直角三角形 ‎∵PO是公共边，PA=PB=PC ‎∴△POA≌△POB≌△POC ‎∴OA=OB=OC 故O是△ABC外心 故选D．‎ ‎【点评】本题是立体几何中一道证明题，考查了线面垂直的定义与三角形的全等．‎ ‎　‎ ‎12．（5分）若直线y=kx+4+2k与曲线 有两个交点，则k的取值范围是（　　）‎ A．[1，+∞） B．[﹣1，﹣） C．（，1] D．（﹣∞，﹣1]‎ ‎【分析】将曲线方程变形判断出曲线是上半圆；将直线方程变形据直线方程的点斜式判断出直线过定点；画出图形，数形结合求出满足题意的k的范围．‎ ‎【解答】解：曲线 即x2+y2=4，（y≥0）‎ 表示一个以（0，0）为圆心，以2为半径的位于x轴上方的半圆，如图所示：‎ 直线y=kx+4+2k即y=k（x+2）+4‎ 表示恒过点（﹣2，4）斜率为k的直线 结合图形可得 ‎，‎ ‎∵解得 ‎∴要使直线与半圆有两个不同的交点，k的取值范围是 故选B ‎【点评】解决直线与二次曲线的交点问题，常先化简曲线的方程，一定要注意做到同解变形，数形结合解决参数的范围问题 ‎　‎ 二、填空题（本题共4小题，每小题5分，共20分.）‎ ‎13．（5分）点A（2，1）到直线x﹣y+1=0的距离为　　．‎ ‎【分析】直接由点到直线的距离公式求点A（2，1）到直线x﹣y+1=0的距离．‎ ‎【解答】解：由点到直线的距离公式，得点A（2，1）到直线x﹣y+1=0的距离d=．‎ 故答案为．‎ ‎【点评】本题考查了点到直线的距离公式，解答的关键是熟记公式，是基础题．‎ ‎　‎ ‎14．（5分）已知直线过点（1，1），且在两个坐标轴上的截距相等，则该直线的方程为　y=x或y=2﹣x　．‎ ‎【分析】直线过点（1，1），且在两个坐标轴上的截距相等，可设出直线l的点斜式方程，利用截距相等列式相等解之即可．‎ ‎【解答】解：∵直线l过点（1，1），且在两个坐标轴上的截距相等，‎ ‎∴直线l的斜率存在且不为0，设为k，则k≠0，‎ ‎∴直线l的方程为：y﹣1=k（x﹣1），‎ 令x=0，y=1﹣k；‎ 令y=0，x=1﹣，‎ 依题意，1﹣k=1﹣，‎ ‎∴k2=1，‎ ‎∴k=±1．‎ ‎∴该直线的方程为y=x或y=2﹣x．‎ 故答案为：y=x或y=2﹣x．‎ ‎【点评】本题考查直线的截距式方程，考查分类讨论思想与运算能力，属于基础题．‎ ‎　‎ ‎15．（5分）若正三棱柱的所有棱长均为a，且其体积为16，则a=　4　．‎ ‎【分析】由题意可得（•a•a•sin60°）•a=16，由此求得a的值．‎ ‎【解答】解：由题意可得，正棱柱的底面是变长等于a的等边三角形，面积为•a•a•sin60°，正棱柱的高为a，‎ ‎∴（•a•a•sin60°）•a=16，∴a=4，‎ 故答案为：4．‎ ‎【点评】本题主要考查正棱柱的定义以及体积公式，属于基础题．‎ ‎　‎ ‎16．（5分）若圆x2+y2=r2（r＞0）上恰有相异的两点到直线4x﹣3y+25=0的距离等于，则r的取值范围是　（5﹣，5+）　．‎ ‎【分析】求出圆心到直线的距离，使得圆心到直线的距离与半径的差的绝对值小于，即可满足题意．‎ ‎【解答】解：圆心O（0，0）到直线4x﹣3y+25=0的距离d==5，‎ ‎∵圆x2+y2=r2（r＞0）上恰有相异两点到直线4x﹣3y+25=0的距离等于1，‎ ‎∴|d﹣r|＜，即|5﹣r|＜，‎ ‎∴r∈（5﹣，5+）．‎ 故答案为（5﹣，5+）．‎ ‎【点评】本题考查了直线与圆的位置关系，注意题目条件的转化是解题的关键，考查计算能力．‎ ‎　‎ 三、解答题：（共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（12分）三角形的三个顶点为A（4，0），B（6，5），C（0，3）．‎ ‎（1）求BC边上高所在直线的方程；‎ ‎（2）求BC边上中线所在直线的方程．‎ ‎【分析】（1）运用直线的斜率公式可得直线BC的斜率，再由两直线垂直的条件：斜率之积为﹣1，可得BC边上高的斜率，再由点斜式方程，即可得到所求直线的方程；‎ ‎（2）运用中点坐标公式可得BC的中点M，求出AM的斜率，由点斜式方程即可得到所求中线的方程．‎ ‎【解答】解：（1）△ABC的三个顶点是A（4，0），B（6，5），C（0，3），‎ 可得BC边所在直线的斜率kBC==，‎ 因为BC所在直线的斜率与BC高线的斜率乘积为﹣1，‎ 所以BC高线的斜率为﹣3，‎ 又因为BC高线所在的直线过A（4，0），‎ 所以BC高线所在的直线方程为y﹣0=﹣3（x﹣4），‎ 即3x+y﹣12=0；‎ ‎（2）设BC中点为M，‎ 则中点M（3，4），‎ kAM==﹣4，‎ 所以BC边上的中线AM所在的直线方程为y﹣0=﹣4（x﹣4），‎ 即为4x+y﹣16=0．‎ ‎【点评】本题考查直线方程的求法，注意运用两直线垂直的条件：斜率之积为﹣1，以及中点坐标公式，考查运算能力，属于基础题．‎ ‎　‎ ‎18．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥面ABCD，E、F分别为PB、PD的中点，‎ ‎（1）求证：EF∥面ABCD；‎ ‎（2）求证：BD⊥面PAC．‎ ‎【分析】（1）连接AC，BD，由已知可得EF∥‎ BD，由线面平行的判定定理，可得EF∥面ABCD；‎ ‎（2）由线面垂直的定义，可得PA⊥BD，由正方形的性质，可得AC⊥BD，再由线面垂直的判定定理，可得：BD⊥面PAC．‎ ‎【解答】证明：（1）连接AC，BD，‎ 在△PBD中，E，F分别为PB、PD的中点，‎ ‎∴EF∥BD，‎ ‎∵EF⊄面ABCD，BD⊂面ABCD；‎ ‎∴EF∥面ABCD；‎ ‎（2）∵PA⊥面ABCD，BD⊂面ABCD ‎∴PA⊥BD，‎ ‎∵底面ABCD为正方形，‎ ‎∴AC⊥BD，‎ 又∵PA∩AC=C，PA，AC⊂面PAC，‎ ‎∴BD⊥面PAC．‎ ‎【点评】本题考查的知识点是线面平行的判定，线面垂直的判定，难度中档．‎ ‎　‎ ‎19．（12分）（1）已知△AOB的顶点坐标分别是A（4，0），B（0，4），O（0，0），求△AOB外接圆的方程；‎ ‎（2）已知圆C的半径为2，圆心在x轴的正半轴上，直线3x+4y+4=0与圆C相切，求圆C的方程为．‎ ‎【分析】（1）设三角形AOB的外接圆的方程为：x2+y2+Dx+Ey+F=0，把A（4，0），B（0，4），O（0，0）三点代入能求出圆的方程．‎ ‎（2）直线与圆相切，设圆心坐标为（a，0），则圆方程为（x﹣a）2+y2‎ ‎=4，由已知得d=R=2=，由此能求出圆C的方程．‎ ‎【解答】解：（1）设△AOB的外接圆的方程为：‎ x2+y2+Dx+Ey+F=0，‎ 把A（4，0），B（0，4），O（0，0）三点代入，得：‎ ‎，‎ 解得D=﹣4，E=﹣4，F=0，‎ ‎∴△AOB外接圆的方程为x2+y2﹣4x﹣4y=0．‎ ‎（2）直线与圆相切，设圆心坐标为（a，0），‎ 则圆方程为：‎ ‎（x﹣a）2+y2=4，‎ ‎∵圆心与切点连线必垂直于切线，‎ 根据点与直线距离公式，得d=R=2=，‎ 解得a=2或a=﹣，（因圆心在正半轴，不符合舍去）‎ ‎∴a=2，‎ ‎∴圆C的方程为：（x﹣2）2+y2=4．‎ ‎【点评】本题考查圆的方程的求法，是基础题，解题时要认真审题，注意待定系数法的合理运用．‎ ‎　‎ ‎20．（12分）已知平行四边形ABCD中，AB=2，E为AB的中点，且△ADE是等边三角形，沿DE把△ADE折起至A1DE的位置，使得A1C=2．‎ ‎（1）F是线段A1C的中点，求证：BF∥平面A1DE；‎ ‎（2）求证：A1D⊥CE；‎ ‎（3）求点A1到平面BCDE的距离．‎ ‎【分析】（1）取A1D的中点G，连结EG，FG，推导出四边形BFGE是平行四边形，从而BF∥EG，由此能证明BF∥平面A1DE．‎ ‎（2）推导出CE⊥DE，CE⊥A1E，从而CE⊥平面A1DE，由此能证明A1D⊥CE．‎ ‎（3）设点A1到平面BCDE的距离为h，由，能求出点A1到平面BCDE的距离．‎ ‎【解答】证明：（1）取A1D的中点G，连结EG，FG，‎ ‎∵F为A1C的中点，∴FG∥CD，且FG=，‎ ‎∵BE∥CD，且BE=，∴FGBE，‎ ‎∴四边形BFGE是平行四边形，∴BF∥EG，‎ ‎∵EG⊂平面A1DE，BF⊄平面A1DE，‎ ‎∴BF∥平面A1DE．‎ ‎（2）折叠前，∠AED=60°，∠CEB=∠ECB=30°，∴∠CED=90°，‎ 在四棱锥A1﹣BCDE中，CE⊥DE，‎ 在△BCE中，BC=BE=1，∠B=120°，‎ 由余弦定理得CE=，‎ 又A1E=1，A1C=2，由勾股定理的逆定理得∠CEA1=90°，‎ ‎∴CE⊥A1E，∵DE∩A1E=E，∴CE⊥平面A1DE，‎ ‎∵A1D⊂平面A1DE，∴A1D⊥CE．‎ 解：（3）由（2）知CE⊥平面A1DE，‎ 设点A1到平面BCDE的距离为h，‎ 由，得，‎ ‎∴，‎ 解得h=．‎ ‎∴点A1到平面BCDE的距离为．‎ ‎【点评】本题考查线面平行、线线平行的证明，考查点到平面的距离的求法，考查学生的运算能力及推理转化能力，属中档题．‎ ‎　‎ ‎21．（12分）已知过点A（0，﹣1）且斜率为k的直线l与圆C：（x﹣2）2+（y﹣3）2=4交于M，N两点．‎ ‎（1）求k的取值范围；‎ ‎（2）若，其中O为坐标原点，求MN的长度．‎ ‎【分析】（1）联立方程组，令判别式△＞0得出k的范围；‎ ‎（2）根据根与系数的关系列方程得出k的值，代入弦长公式计算MN．‎ ‎【解答】解：（1）直线l的方程为y=kx﹣1，代入圆C的方程得：（1+k2）x2﹣（4+8k）x+16=0，‎ ‎∴△=（4+8k）2﹣64（1+k2）＞0，‎ 解得k＞．‎ ‎（2）设M（x1，y1），N（x2，y2），‎ 则由（1）可知x1x2=，x1+x2=，‎ ‎∴y1y2=k2x1x2﹣k（x1+x2）+1=，‎ ‎∴=x1x2+y1y2==9，‎ 解得k=2．‎ ‎∴MN==•=4．‎ ‎【点评】本题考查了直线与圆的位置关系，平面向量的计算，属于中档题．‎ ‎　‎ ‎22．（10分）已知直线l：kx﹣y+2k+1=0，k∈R．‎ ‎（1）当k变化时，直线l恒过一定点P，求点P的坐标；‎ ‎（2）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值．‎ ‎【分析】（1）由直线l：kx﹣y+2k+1=0，k∈R．变形为：k（x+2）﹣y+1=0，令，解得定点坐标．‎ ‎（2）直线l交x轴负半轴于点A（﹣，0），交y轴正半轴于点B（0，2k+1），则，k≠0，解得k＞0．△AOB的面积为S=×=，利用基本不等式的性质即可得出．‎ ‎【解答】解：（1）由直线l：kx﹣y+2k+1=0，k∈R．变形为：k（x+2）﹣y+1=0，令，解得x=﹣2，y=1．‎ ‎（2）直线l交x轴负半轴于点A（﹣，0），交y轴正半轴于点B（0，2k+1），则，k≠0，解得k＞0．‎ 设△AOB的面积为S=×=≥=4，当且仅当k=时取等号．‎ ‎∴S的最小值为4．‎ ‎【点评】本题考查了直线交点、三角形面积、基本不等式的性质，考查了推理能力与计算能力，属于中档题．‎ ‎　‎