2018-2019学年河北省唐山市玉田县高一下学期期中数学试题（解析版）

2018-2019学年河北省唐山市玉田县高一下学期期中数学试题（解析版）

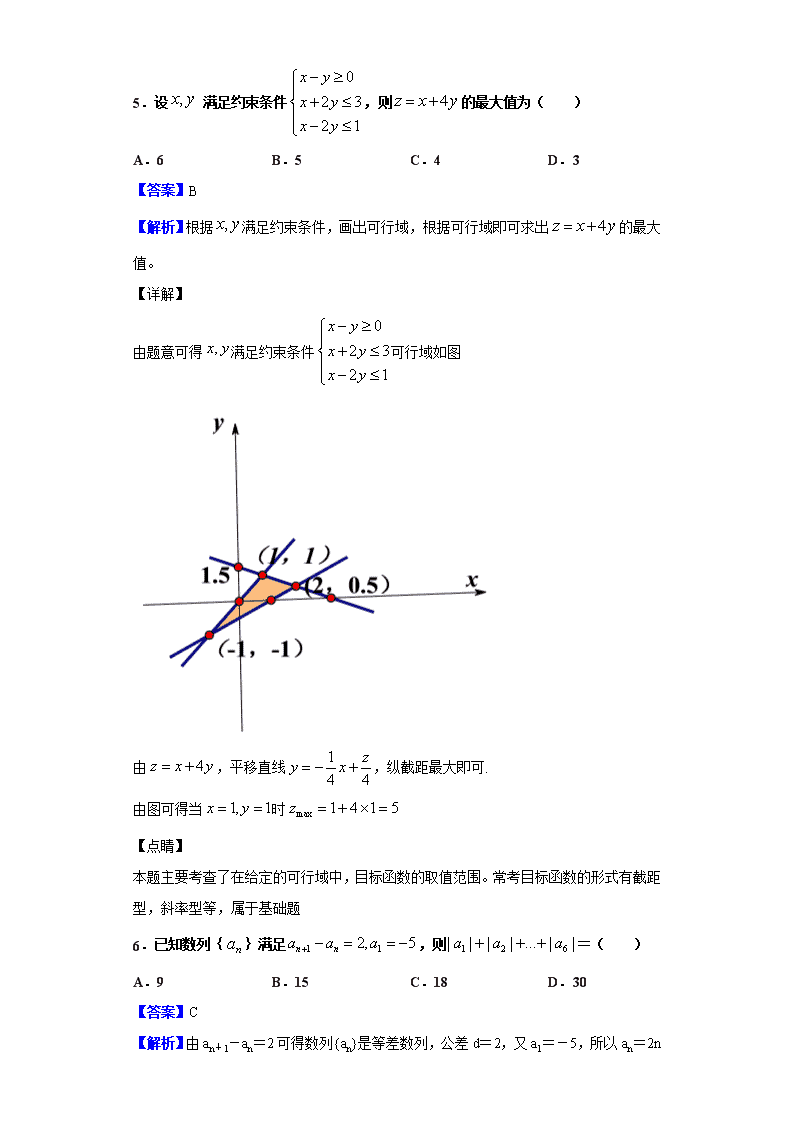
‎2018-2019学年河北省唐山市玉田县高一下学期期中数学试题 一、单选题 ‎1．如果a＜b＜0，那么下列不等式成立的是（　　）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】1、根据不等式的性质利用作差法即可得出答案。2、取特殊值（即取一个具体的值），只需满足,即可排除ABC答案。‎ ‎【详解】‎ 法一:根据不等式的性质得，A错误。因为，又因为，所以错误。因为，所以由基本不等式得（当且仅当时取等）C错误。由前面可知A错误，因此，所以，D对 法二：特殊值法：取，A答案（不对）。B答案 （不对）。C.答案（不对），因此选择D。‎ ‎【点睛】‎ 本题主要考查了不等式的基本性质，比较两个数的大小常用的方法有作差法、作商法等。做选择题常用方法：特殊值法，代入法等。特殊值法能快速的解决本题。‎ ‎2．等差数列中，已知，，则的值是（　　）‎ A．30 B．27 C．24 D．21‎ ‎【答案】B ‎【解析】根据等差数列的性质可以得到，故公差，而所求式子为，由此求得相应的值.‎ ‎【详解】‎ 根据等差数列的性质可以得到，故公差，而所求式子为 ‎，故选B.‎ ‎【点睛】‎ 本小题主要考查等差数列的一个性质：若为等差数列，且，则有，再求得数列的公差，即可求得所要求解表达式的值.‎ ‎3．已知的前n项和为，且，则＝（　　）‎ A．－3 B．1 C．4 D．6‎ ‎【答案】C ‎【解析】根据题意分别取和时带入即可计算出。‎ ‎【详解】‎ 由题意得:当时，。‎ 当时，‎ ‎【点睛】‎ 本题主要考查了前项和以及递推公式。充分理解项和以及递推公式是解决本题的关键。属于基础题。‎ ‎4．的内角的对边分别为，若成等比数列，且,则＝（　　）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由成等比数列，根据等比中项即可得出一个式子，结合带入余弦定理即可。‎ ‎【详解】‎ 因为成等比数列，所以，再由，所以。分别代入余弦定理。‎ ‎【点睛】‎ 本题主要考查了等比中项，余弦定理的应用。属于基础题。‎ ‎5．设 满足约束条件，则的最大值为（　　）‎ A．6 B．5 C．4 D．3‎ ‎【答案】B ‎【解析】根据满足约束条件，画出可行域，根据可行域即可求出的最大值。‎ ‎【详解】‎ 由题意可得满足约束条件可行域如图 由，平移直线，纵截距最大即可.‎ 由图可得当时 ‎【点睛】‎ 本题主要考查了在给定的可行域中，目标函数的取值范围。常考目标函数的形式有截距型，斜率型等，属于基础题 ‎6．已知数列｛｝满足，则＝（　　）‎ A．9 B．15 C．18 D．30‎ ‎【答案】C ‎【解析】由an＋1－an＝2可得数列{an}是等差数列，公差d＝2，又a1＝－5，所以an ‎＝2n－7，所以|a1|＋|a2|＋|a3|＋|a4|＋|a5|＋|a6|＝5＋3＋1＋1＋3＋5＝18.‎ ‎7．如图，为测一树的高度，在地面上选取 两点，从两点分别测得树尖的仰角为30°、45°，且两点之间的距离为，则的高度为（　　）‎ A．（30＋30）m B．（30＋15）m C．（15＋30）m D．（15＋3）m ‎【答案】A ‎【解析】试题分析：在中，,由正弦定理得:,树的高度为, 故选A.‎ ‎【考点】1、仰角的定义及两角和的正弦公式；2、阅读能力、建模能力及正弦定理的应用.‎ ‎【思路点睛】本题主要考查仰角的定义及两角和的正弦公式、阅读能力、建模能力及正弦定理的应用，属于难题.与实际应用相结合的题型也是高考命题的动向，这类问题的特点是通过现实生活的事例考查书本知识，解决这类问题的关键是耐心读题、仔细理解题，只有吃透题意，才能将实际问题转化为数学模型进行解答.解答本题的关键是将现实生活中的“树高”问题转化为书本知识“三角函数”的问题.‎ ‎8．已知一个等比数列首项为1，项数是偶数，其奇数项之和为341，偶数项之和为682，则这个数列的项数为（　　）‎ A．4 B．6 C．8 D．10‎ ‎【答案】D ‎【解析】设等比数列项数为2n项,所有奇数项之和为S奇 ‎,所有偶数项之和为S偶，‎ 则S奇=341,S偶=682,所以 ，‎ ‎∴ ，解得n=5，‎ 这个等比数列的项数为10，‎ 本题选择D选项.‎ ‎9．在中，，BC边上的高等于,则（　　）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】试题分析：设 ‎,故选C.‎ ‎【考点】解三角形.‎ ‎10．若函数在处取最小值，则等于(　 　)‎ A． B．1或3 C．3 D．4‎ ‎【答案】C ‎【解析】分析：根据基本不等式中等号成立的条件可得所求．‎ 详解：∵，‎ ‎∴．‎ ‎∴，当且仅当且，即时等号成立．‎ ‎∴．‎ 故选C．‎ 点睛：应用基本不等式求最值时，一定要注意不等式的使用条件“一正、二定、三相等”，若条件不满足，则可根据“拼、凑”等方式进行变形，使得满足应用不等式的条件，解题时特别要注意等号能否成立．‎ ‎11．在中，角的对边分别为，且，若的外接圆的半径为2，则的面积的最大值为（　　）‎ A． B．2 C．4 D．4‎ ‎【答案】A ‎【解析】首先根据正弦定理带入，即可计算出角，由外接圆半径即可得出边长于对应角的正弦值的关系。知道一个角求面积则根据,再结合基本不等式即可求出的面积的最大值。‎ ‎【详解】‎ 由正弦定理得，‎ 又在中有 又三角形的内角和为，‎ 又 当时，取到最大值1‎ ‎【点睛】‎ 本题主要考查了解三角形的问题，关于解三角形常考查的知识点有:正弦定理、余弦定理、三角形内角和、两角的和与差等。题目中出现求最值时，大多时候转化成同一个三角函数结合图形求最值。本题属于难度较大的题。‎ ‎12．若 是函数 的两个不同的零点，且 这三个数可适当排序后成等差数列，也可适当排序后成等比数列，则 的值等于（ ）‎ A．6 B．7 C．8 D．9‎ ‎【答案】D ‎【解析】试题分析：由题意可得：a+b=p，ab=q，‎ ‎∵p＞0，q＞0，‎ 可得a＞0，b＞0，‎ 又a，b，-2这三个数可适当排序后成等差数列，也可适当排序后成等比数列，‎ 可得①或②．‎ 解①得： ；解②得： ．‎ ‎∴p=a+b=5，q=1×4=4，‎ 则p+q=9．‎ ‎【考点】等比数列的性质；等差数列的性质 二、填空题 ‎13．已知等比数列的前项和为，且，则数列的公比的值为____‎ ‎【答案】2或-3‎ ‎【解析】根据等比数列的通项公式及前项和为把转化成和公比的关系即可解出 ‎【详解】‎ 因为等比数列满足，所以，即 ‎【点睛】‎ 本题主要考查了等比数列的前项和为以及通项式。能够熟练的应用等比数列的前项和为以及通项式是解决本题的关键。本题属于基础题。‎ ‎14．在中，角的对边分别为，若，则的形状是____‎ ‎【答案】等腰或直角三角形 ‎【解析】试题分析：根据正弦定理及，可得即，所以,即或,又,所以或,因此的形状是等腰或直角三角形.‎ ‎【考点】正弦定理．‎ ‎15．设等差数列的前项和为，若，则 ＝_______‎ ‎【答案】5‎ ‎【解析】因为差数列的前项和为，，所以公差，，得，解得，故答案为.‎ ‎16．某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨，B原料2吨；生产每吨乙产品要用A原料1吨，B原料3吨；销售每吨甲产品可获得利润3万元，每吨乙产品可获得利润2万元。该企业在一个生产周期内消耗A原料不超过13吨，B原料不超过18吨。那么该企业可获得最大利润为_________‎ ‎【答案】17万元 ‎【解析】根据题意列出满足题目的不等式和目标函数，求目标函数的最值即可。‎ ‎【详解】‎ 设该企业生产甲产品吨，生产乙产品吨。由题意列出方程组，目标函数为。‎ 作出可行域如图所示：当目标函数图象经过点时，该企业获得最大利润为万元。‎ ‎【点睛】‎ 本题主要考查线性规划约束条件中关于最值的计算。解决此类题通常根据题目列出不等式以及目标函数。根据不等式画出可行区域，即可得出目标函数的最值。‎ 三、解答题 ‎17．已知等差数列的前项和为，且。‎ ‎（1）求数列的通项公式；‎ ‎（2）求使不等式成立的的最小值。‎ ‎【答案】(1) .‎ ‎(2)15.‎ ‎【解析】试题分析：（1）设出公差d，由已知得到公差和首项的方程组，求出通项公式；（2）Sn＞an 是一个关于n的二次不等式，先解出n的范围，然后根据n是正整数，可得其最小值.‎ 试题解析：（1）设{an}的公差为d，依题意，‎ 有．‎ 联立得，解得．‎ ‎∴an＝－6＋（n－1）·1＝n－7．n∈N ‎（2）∵an＝n－7，．‎ 令，即，‎ 解得n＜1或n＞14．‎ 又n∈N，∴n＞14．‎ ‎∴n的最小值为15．‎ ‎【考点】等差数列通项公式与前n项和，二次不等式 ‎18．已知的内角的对边长分别为，且。‎ ‎（1）求角的大小；‎ ‎（2）若，的周长为6，求该三角形的面积。‎ ‎【答案】（1）（2）‎ ‎【解析】（1）根据正弦定理以及三角形内角和的关系化简即可。‎ ‎（2）由的周长为6，即可得出，再根据（1）的结果，利用余弦定理把整体计算出来，根据即可。‎ ‎【详解】‎ 解：（1）在中，∵∴ ‎ 即： ‎ ‎∴则： ∵∴‎ ‎（2）由于，三角形的周长为6，故 ‎ 由余弦定理有 所以 所以三角形的面积 ‎【点睛】‎ 本题主要是考查解三角形的题。题目中出现即有边长，又有角的正弦（余弦）时，通常根据正弦定理先化简，在求三角形面积时，通常结合余弦定理利用整体的思想即可得出或或，.或者通过解方程直接求出。从而即可计算出面积。‎ ‎19．已知等比数列满足 ‎（1）求的通项公式；‎ ‎（2）设，求数列前项和。‎ ‎【答案】（1）（2）‎ ‎【解析】（1）把和换成和的关系即可。‎ ‎（2）首先利用列项把计算出来，再根据错位相减即可得出前项和 ‎【详解】‎ 解：（1）设，依题意，有 ‎ 解得 ‎ 所以 ‎（2）‎ ‎ ‎ 记数列的前n项的和为，则 两式相减，得 故 ‎【点睛】‎ 本题主要考查了数列通项的求法以及数列前项和的求法。数列通项的求法常用的方法有：公式法、累加、累乘等。求数列前项和的常用的方法有：错位相减、列项相消、分组求和等。‎ ‎20．某种商品原来每件售价为25元，年销售量8万件．‎ ‎（1）据市场调查，若价格每提高1元，销售量将相应减少2000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？‎ ‎（2）为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到元．公司拟投入万元作为技改费用，投入50万元作为固定宣传费用，投入万元作为浮动宣传费用．试问：当该商品明年的销售量a至少应达到多少万件时，才可能使明年的销售收入不低于原收入与总投入之和？并求出此时商品的每件定价．‎ ‎【答案】（1）每件定价最多为元；（2）当该商品明年的销售量至少达到万件时，才可能使明年的销售收入不低于原收入与总收入之和，此时该商品的每件定价为元．‎ ‎【解析】（1）设出每件的定价，根据“销售的总收入不低于原收入”列不等式，解不等式求得定价的取值范围，由此求得定价的最大值.（2）利用题目所求“改革后的销售收入不低于原收入与总投入之和”列出不等式，将不等式分离常数 ‎，然后利用基本不等式求得的取值范围以及此时商品的每件定价.‎ ‎【详解】‎ 解：（1）设每件定价为元，‎ 依题意得，‎ 整理得，‎ 解得 所以要使销售的总收入不低于原收入，每件定价最多为40元.‎ ‎（2）依题意知当时，不等式有解 等价于时，有解，‎ 由于，‎ 当且仅当，即时等号成立，‎ 所以 当该商品改革后销售量至少达到10.2万件时，才可能使改革后的销售收入不低于原收入与总投入之和，此时该商品的每件定价为30元.‎ ‎【点睛】‎ 本小题主要考查实际应用问题，考查一元二次不等式的解法，考查利用基本不等式求最小值，属于中档题.‎ ‎21．如图，在平面四边形中，已知，，在上取点，使得，连接，若， 。‎ ‎（1）求 的值；‎ ‎（2）求的长。‎ ‎【答案】（1）；（2）.‎ ‎【解析】试题分析：（1）在中，直接由正弦定理求出；（2）在 中，，，可求出，在中，直接由余弦定理可求得.‎ 试题解析：（1）在中，据正弦定理，有.‎ ‎∵，，，‎ ‎∴.‎ ‎（2）由平面几何知识，可知，在中，∵，，‎ ‎∴.‎ ‎∴.‎ 在中，据余弦定理，有 ‎∴‎ 点睛：此题考查了正弦定理、余弦定理的应用，利用正弦、余弦定理可以很好得解决了三角形的边角关系，熟练掌握定理是解本题的关键．在中，涉及三边三角，知三（除已知三角外）求三，可解出三角形，当涉及两边及其中一边的对角或两角及其中一角对边时，运用正弦定理求解；当涉及三边或两边及其夹角时，运用余弦定理求解.‎ ‎22．已知数列的前项和为，，且，，（）‎ ‎（1）求，并证明：当时， ． ‎ ‎（2）求以及。‎ ‎【答案】（1）；见证明；（2）的值见解析；‎ ‎【解析】（1）取代入即可求出，要证明，只需要把换成之间的关系即可。‎ ‎（2）根据（1）的结果，分奇数项和偶数项，把求出来即可。‎ ‎【详解】‎ ‎（1）当，由及，得．‎ 当时，由，得．‎ 因为，所以． ‎ ‎（2）由（1）知数列的奇数项成公差为2的等差数列，偶数项成公差为2等差数列，‎ 故 ‎ 当时，‎ ‎；‎ 当时，‎ 故 ‎【点睛】‎ 本题主要考查了已知递推关系求其中某一项以及数列的前项和的问题，对于本题需要把奇数项和偶数项分别求，是本题的难点。在解决此类问题时一定要找清楚奇数项和偶数项。属于难度比较大的题。‎