2019-2020学年安徽省滁州市定远县育才学校高二（普通班）上学期第一次月考数学（理）试题 Word版

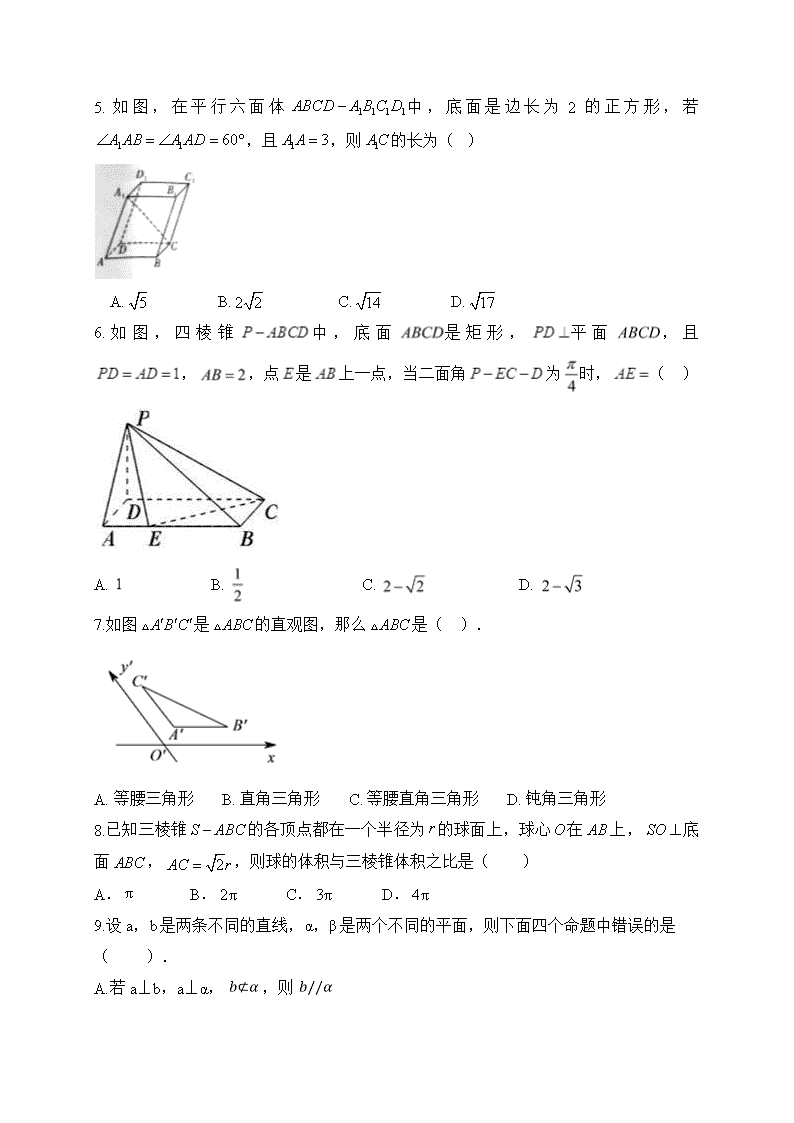
2019-2020学年安徽省滁州市定远县育才学校高二（普通班）上学期第一次月考数学（理）试题 Word版

滁州市定远县育才学校2019-2020学年度上学期第一次月考卷 高二普通班数学（理科）‎ 一、选择题(共12小题,每小题5分,共60分) ‎ ‎1.已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题： ①若α⊥β，m∥α，则m⊥β； ②若m⊥α，n⊥β，且m⊥n，则α⊥β； ③若m⊥β，m∥α，则α⊥β； ④若m∥α，n∥β，且m∥n，则α∥β． 其中正确命题的个数是（   ） A.1 B‎.2 C.3 D.4‎ ‎2.在正方体中， 和分别为、的中点，那么异面直线与所成角的大小为（ ）‎ A. B. C. D. ‎ ‎3.如图是某个集合体的三视图，则这个几何体的表面积是（ ） A. B. C. D.‎ ‎4.设表示平面， 表示直线，则下列命题中，错误的是( )‎ A. 如果，那么内一定存在直线平行于 B. 如果， ， ，那么 C. 如果不垂直于，那么内一定不存在直线垂直于 D. 如果，那么内所有直线都垂直于 ‎5.如图，在平行六面体中，底面是边长为2的正方形，若，且，则的长为（ ）‎ A. B. C. D.‎ ‎6.如图，四棱锥中，底面是矩形，平面，且，，点是上一点，当二面角为时，（ ）‎ A. B. C. D. ‎ ‎7.如图是的直观图，那么是（ ）．‎ ‎ ‎ A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 钝角三角形 ‎8.已知三棱锥的各顶点都在一个半径为的球面上，球心在上，底面，，则球的体积与三棱锥体积之比是（　　）‎ A． B． C． D．‎ ‎9.设a，b是两条不同的直线，α，β是两个不同的平面，则下面四个命题中错误的是（ ）． A.若a⊥b，a⊥α， ，则 ‎ ‎ B.若a⊥b，a⊥α，b⊥β，则α⊥β C.若a⊥β，α⊥β，则 或 D.若 ， ，则 ‎ ‎10.《九章算术》是我国古代著名数学经典.其中对勾股定理的论术比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺.问这块圆柱形木料的直径是多少？长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）.已知弦尺，弓形高寸，估算该木材镶嵌在墙中的体积约为（ ）‎ ‎（注：1丈=10尺=100寸， ， ）‎ A. 633立方寸 B. 620立方寸 C. 610立方寸 D. 600立方寸 ‎11.正四棱柱中， ，则与平面所成角的正弦值为（ ）‎ A. B. C. D. ‎ ‎12.如图，棱长为1的正方体中， 是侧面对角线， 上一点，若是菱形，则其在底面上投影的四边形面积（ ）‎ A. B. C. D. ‎ 二、填空题(共4小题,每小题5分,共20分) ‎ ‎13.已知一个圆台的上、下底面半径分别为，高为，则该圆台的母线长为__________．‎ ‎14.如图，三棱柱的侧棱长和底面边长均为，且侧棱底面，其正（主）视图是边长为的正方形，则此三棱柱侧（左）视图的面积为__________．‎ ‎ ‎ ‎15.已知三棱锥的所有顶点都在球的球面上， 是边长为1的正三角形， 为球的直径，该三棱锥的体积为，则球的表面积为__________．‎ ‎16.如图，在边长为4的正方形纸片中， 与相交于点，剪去，将剩余部分沿折叠，使重合，则折叠后以为顶点的四面体的体积为__________．‎ 三、解答题(共6小题,共70分) ‎ ‎17.（12分）如图，将直角沿着平行边的直线折起，使得平面平面，其中、分别在、边上，且，，，点为点折后对应的点，当四棱锥的体积取得最大值时，求的长.‎ ‎18. （10分）如图，在四边形ABCD中，，，，，AD=2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.‎ ‎19. （12分）如图，在三棱柱中， 平面， 为正三角形， ， 为的中点．‎ ‎（1）求证：平面平面；‎ ‎（2）求三棱锥的体积．‎ ‎20. （12分）如图，四棱锥的底面是正方形，⊥底面，，分别为，的中点．‎ ‎（1）求证：平面；‎ ‎（2）若，求三棱锥的体积．‎ ‎21.（12分）底面边长为2的正三棱锥,其表面展开图是三角形，如图，求△的各边长及此三棱锥的体积.‎ ‎22. （12分）如图,在直三棱柱中,,,,点是的中点.‎ ‎(1)求证：面； ‎ ‎(2)求直线与平面所成角的余弦值.‎ 参考答案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B C B D A D B D D A A B ‎13. 14. 15. 16.‎ ‎17.解：由勾股定理易求得，设，则.‎ 因为，所以，‎ 则四棱锥的体积为，‎ 所以，当时，，递增；‎ 当时，，递减.故当，即时，取得最大值.‎ ‎18. 解：四边形绕旋转一周所成的几何体如图： ‎ ‎ ‎ ‎19. 解：（Ⅰ）证明：因为底面，所以 因为底面正三角形， 是的中点,所以 因为，所以平面 因为平面平面,所以平面平面 ‎（Ⅱ）由（Ⅰ）知中， ， ‎ 所以 所以 ‎20.解：（1）取的中点为，连接，，可证明，‎ ‎∴平面．‎ ‎（2）．‎ ‎21. 解：由题意中， ， ，所以是的中位线，因此是正三角形，且边长为4．‎ 即，三棱锥是边长为2的正四面体 ‎∴如右图所示作图，设顶点在底面内的投影为，连接，并延长交于 ‎∴为中点， 为的重心， 底面 ‎∴， ， ‎ ‎22.（1）证明：如图，以{AB，AC，AA1}为单位正交基底建立空间直角坐标系A-xyz，‎ 则A（0，0，0），B（2，0，0），C（0，2，0），A1（0，0，4），D（1，1，0），B1（2，0，4），C1（0，2，4）‎ ‎∴＝(2，0，−4)，＝(1，1，0)，＝(0，2，4)，‎ 设平面的法向量为＝(x，y，z)，由 ‎∴取z=1，得y=-2，x=2，∴平面ADC1的法向量为＝(2，−2，1)‎ 由此可得，＝2×2+0×(−2)+(−4)×1＝0，又A1B⊄平面ADC1，∴A1B∥面ADC1.‎ ‎（2）解：＝(−2，2，0)，设直线与平面所成角为θ，则，‎ 又θ为锐角，∴直线与平面所成角的余弦值为