高考数学专题复习课件：4-4　函数y＝Asin(ωx＋φ)的图象及应用

高考数学专题复习课件：4-4　函数y＝Asin(ωx＋φ)的图象及应用

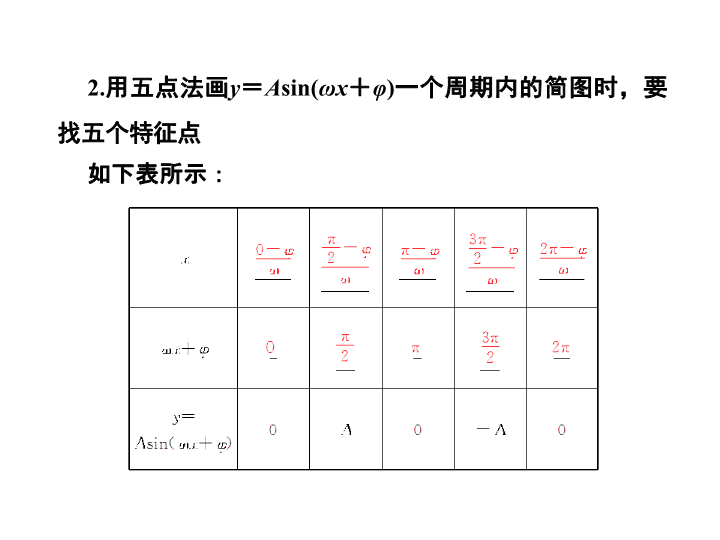
§4.4 　函数 y ＝ A sin( ωx ＋ φ ) 的图象及应用 [ 考纲要求 ] 　 1. 了解函数 y ＝ A sin( ωx ＋ φ ) 的物理意义；能画出 y ＝ A sin( ωx ＋ φ ) 的图象，了解参数 A ， ω ， φ 对函数图象变化的影响； 2. 了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题． 1 ． y ＝ A sin( ωx ＋ φ ) 的有关概念 2. 用五点法画 y ＝ A sin( ωx ＋ φ ) 一个周期内的简图时，要找五个特征点 如下表所示： 3. 函数 y ＝ sin x 的图象经变换得到 y ＝ A sin( ωx ＋ φ )( A ＞ 0 ， ω ＞ 0) 的图象的步骤如下： 【 答案 】 (1) × 　 (2) √ 　 (3) √ 　 (4) × 　 (5) √ 【 答案 】 A 【 答案 】 A 【 答案 】 D 【 答案 】 A 探究 2 在本例条件下，如何由 y ＝ sin x 的图象变换得到 y ＝ f ( x ) 的图象？ 【 答案 】 (1)D 　 (2)B 【 答案 】 C 【 答案 】 ( － 2 ，－ 1) 【 引申探究 】 例 4 中， “ 有两个不同的实数根 ” 改成 “ 有实根 ” ，则 m 的取值范围是 ________ ． 【 答案 】 [ － 2 ， 1) 【 方法规律 】 (1) 三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型再利用三角函数的有关知识解决问题． (2) 方程根的个数可转化为两个函数图象的交点个数． (3) 研究 y ＝ A sin( ωx ＋ φ ) 的性质时可将 ωx ＋ φ 视为一个整体，利用换元法和数形结合思想进行解题． 【 答案 】 ①③ ► 方法与技巧 1 ．五点法作图及图象变换问题 (1) 五点法作简图要取好五个关键点，注意曲线凸凹方向； (2) 图象变换时的伸缩、平移总是针对自变量 x 而言，而不是看角 ωx ＋ φ 的变化． 2 ．由图象确定函数解析式 由图象确定 y ＝ A sin( ωx ＋ φ ) 时， φ 的确定是关键，尽量选择图象的最值点代入；若选零点代入，应根据图象升降找 “ 五点法 ” 作图中第一个零点． 3 ．对称问题 函数 y ＝ A sin( ωx ＋ φ ) 的图象与 x 轴的每一个交点均为其对称中心，经过该图象上坐标为 ( x ， ± A ) 的点与 x 轴垂直的每一条直线均为其图象的对称轴，这样的最近两点间横坐标的差的绝对值是半个周期 ( 或两个相邻对称中心的距离 ) ． ► 失误与防范 1 ．由函数 y ＝ sin x 的图象经过变换得到 y ＝ A sin( ωx ＋ φ ) 的图象，如先伸缩，再平移时，要把 x 前面的系数提取出来． 2 ．复合形式的三角函数的单调区间的求法．函数 y ＝ A sin( ωx ＋ φ )( A >0 ， ω >0) 的单调区间的确定，基本思想是把 ωx ＋ φ 看做一个整体．若 ω <0 ，要先根据诱导公式进行转化． 3 ．函数 y ＝ A sin( ωx ＋ φ ) 在 x ∈ [ m ， n ] 上的最值可先求 t ＝ ωx ＋ φ 的范围，再结合图象得出 y ＝ A sin t 的值域 .