- 2021-06-24 发布 |
- 37.5 KB |
- 10页


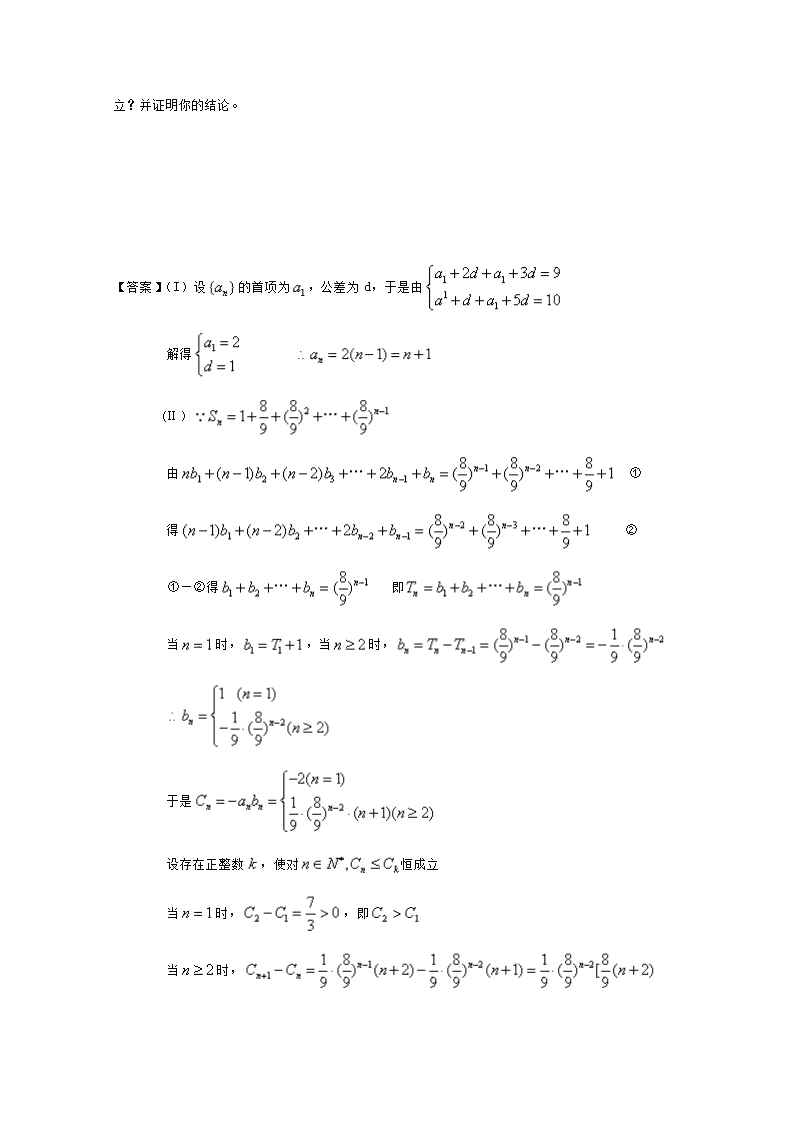
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广东广州市天河区普通高中2018届高考数学一轮复习精选试题:数列(解答题)
全*品*高*考*网, 用后离不了! 数列02 解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤) 1.函数f(x)定义在[0,1]上,满足且f(1)=1,在每个区间=1,2,…)上, y=f(x) 的图象都是平行于x轴的直线的一部分. (Ⅰ)求f(0)及的值,并归纳出)的表达式; (Ⅱ)设直线轴及y=f(x)的图象围成的矩形的面积为, 求a1,a2及的值. 【答案】 (Ⅰ) 由f(0)=2f(0), 得f(0)=0. 由及f(1)=1, 得. 同理, 归纳得 (Ⅱ) 当时, 所以是首项为,公比为的等比数列. 所以 2.已知等差数列满足;又数列满足+…+,其中是首项为1,公比为的等比数列的前项和。 (I)求的表达式; (Ⅱ)若,试问数列中是否存在整数,使得对任意的正整数都有 成立?并证明你的结论。 【答案】(I)设的首项为,公差为d,于是由 解得 (Ⅱ) 由 ① 得 ② ①—②得 即 当时,,当时, 于是 设存在正整数,使对恒成立 当时,,即 当时, 当时,当时,,当时, 存在正整数或8,对于任意正整数都有成立。 3.函数对任意都有 (1)求的值; (2)数列满足:,求; (3)令,试比较与的大小. 【答案】(1)令, 则有 (2)令,得即 因为, 所以 两式相加得: , (3), 时,; 时, =4 =4 4.已知数列为等差数列,且 (1)求数列的通项公式; (2)证明 【答案】(I)设等差数列的公差为d. 由即d=1. 所以即 (II)因为, 所以 5.已知等比数列中,,,. (Ⅰ)求数列的通项公式; (Ⅱ)设,求的最大值及相应的值. 【答案】 (Ⅰ) 由,,所以 . 以. 所以 通项公式为:. (Ⅱ)设,则. 所以,是首项为6,公差为的等差数列. =. 因为是自然数,所以,或时, 最大,其最值是 21. 6.如图,将圆分成个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为。求 (Ⅰ); (Ⅱ)与的关系式; (Ⅲ)数列的通项公式,并证明。 【答案】(Ⅰ) 当时,不同的染色方法种数 , 当时,不同的染色方法种数 , 当时,不同的染色方法种数 , 当时,分扇形区域1,3同色与异色两种情形 ∴不同的染色方法种数 。 (Ⅱ)依次对扇形区域染色,不同的染色方法种数为,其中扇形区域1与不同色的有种,扇形区域1与同色的有种 ∴ (Ⅲ)∵ ∴ ……………… 将上述个等式两边分别乘以,再相加,得 , ∴, 从而。 (Ⅲ)证明:当时, 当时, , 当时, , 故查看更多