数学卷·2018届吉林省辽源市田家炳高级中学高三上学期期中考试（2017

数学卷·2018届吉林省辽源市田家炳高级中学高三上学期期中考试（2017

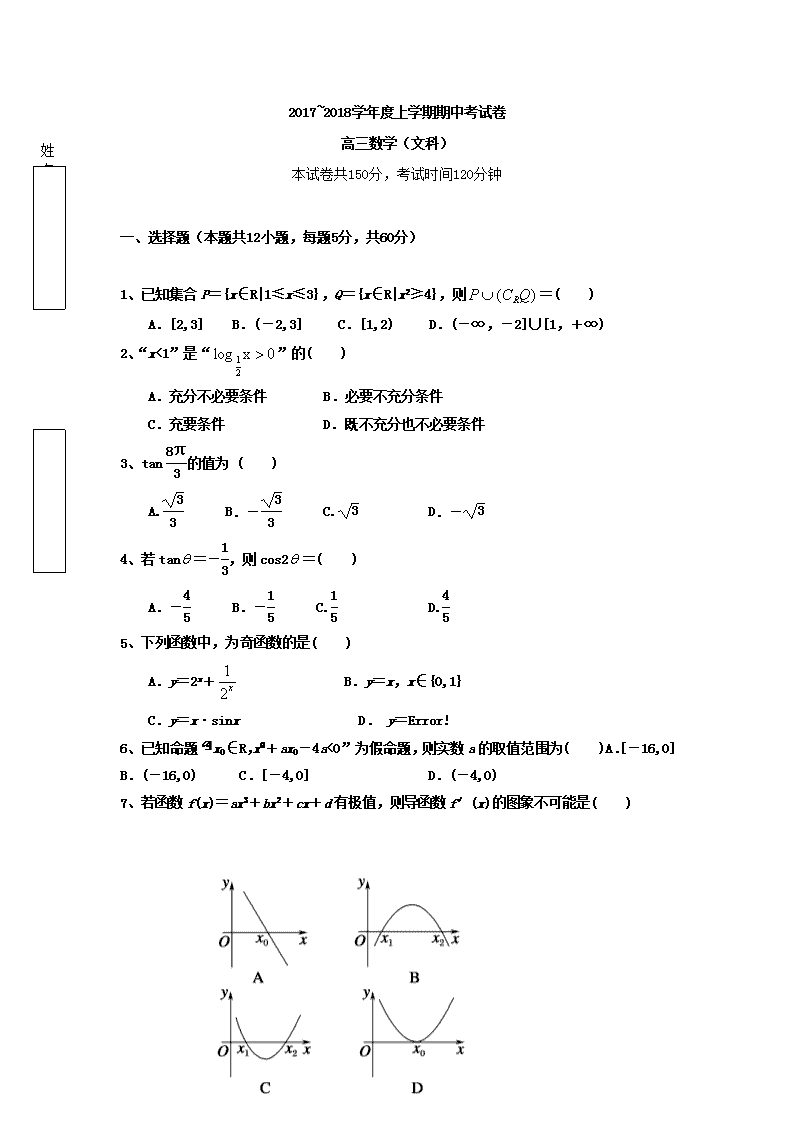
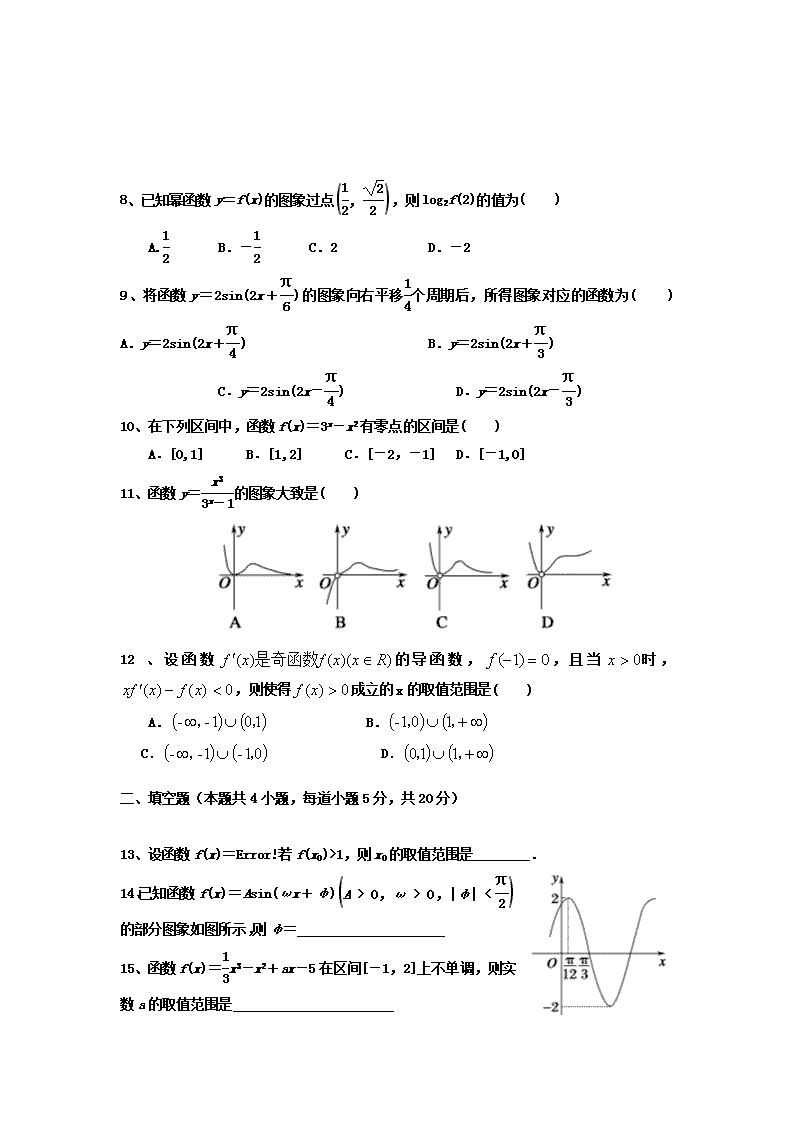
‎2017~2018学年度上学期期中考试卷 姓名 班级 高三数学（文科）‎ 本试卷共150分，考试时间120分钟 一、选择题（本题共12小题，每题5分，共60分）‎ ‎1、已知集合P＝{x∈R|1≤x≤3}，Q＝{x∈R|x2≥4}，则＝(　　)‎ A．[2,3] B．(－2,3] C．[1,2) D．(－∞，－2]∪[1，＋∞)‎ ‎2、“x<1”是“”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎3、tan的值为 (　　)‎ A. B．－ C. D．－ ‎4、若tan＝－，则cos2＝(　　)‎ A．－ B．－ C. D. ‎5、下列函数中，为奇函数的是(　　)‎ A．y＝2x＋ B．y＝x，x∈{0,1}‎ C．y＝x·sinx D． y＝ ‎6、已知命题“∃x0∈R，x＋ax0－4a<0”为假命题，则实数a的取值范围为(　　)A．[－16,0] B．(－16,0) C．[－4,0] D．(－4,0)‎ ‎7、若函数f(x)＝ax3＋bx2＋cx＋d有极值，则导函数f′(x)的图象不可能是(　　)‎ ‎8、已知幂函数y＝f(x)的图象过点，则log2f(2)的值为(　　)‎ A. B．－ C．2 D．－2‎ ‎9、将函数y＝2sin(2x＋)的图象向右平移个周期后，所得图象对应的函数为(　　) A．y＝2sin(2x＋) B．y＝2sin(2x＋)‎ C．y＝2sin(2x－) D．y＝2sin(2x－)‎ ‎10、在下列区间中，函数f(x)＝3x－x2有零点的区间是(　　)‎ A．[0,1] B．[1,2] C．[－2，－1] D．[－1,0]‎ ‎11、函数y＝的图象大致是(　　)‎ ‎12、设函数的导函数，，且当时，，则使得成立的x的取值范围是(　　)‎ A． B．‎ ‎ C． D． ‎ 二、填空题（本题共4小题，每道小题5分，共20分）‎ ‎13、设函数f(x)＝若f(x0)>1，则x0的取值范围是________．‎ ‎14、已知函数f(x)＝Asin(ωx＋φ)的部分图象如图所示，则φ＝ ‎ ‎15、函数f(x)＝x3－x2＋ax－5在区间[－1，2]上不单调，则实数a的取值范围是 ‎ ‎16、当x∈(－∞，－1]时，不等式(m2－m)·4x－2x<0恒成立，则实数m的取值范围是 ‎ 三、解答题（本题共6小题，共 70分）‎ ‎17、已知方程有两个不相等的负根，方程无实数根，若“V”为真，“∧”为假，求的取值范围。‎ ‎18、在△ABC中，内角A，B，C的对边长分别为a，b，c，且(2b－c)cosA＝acosC. (1)求角A的大小；‎ ‎(2)若a＝3，b＝2c，求△ABC的面积．‎ ‎19、已知函数f(x)＝2sinωxcosωx＋cos2ωx(ω>0)的最小正周期为π.‎ ‎(Ⅰ)求ω的值；‎ ‎(Ⅱ)求f(x)的单调递增区间．‎ ‎20、已知函数f(x)＝(k为常数，e是自然对数的底数)，曲线y＝f(x)在点(1，f(1))处的切线与x轴平行．‎ ‎(1)求k的值；‎ ‎(2)求f(x)的单调区间．‎ ‎21、设△ABC的内角A，B，C所对的边分别为a，b，c，满足＝.‎ ‎(1)求角C的大小；‎ ‎(2)设函数f(x)＝cos(2x＋C)，将f(x)的图象向右平移个单位长度后得到函数g(x)的图象，求函数g(x)在区间上的值域．‎ ‎22、已知a∈R，函数f(x)＝ax－lnx，x∈(0，e](其中e是自然对数的底数)．‎ ‎(1)当a＝2时，求f(x)的单调区间和极值；‎ ‎(2)求函数f(x)在区间(0，e]上的最小值．‎ ‎1、B 2、B 3、D 4、D 5、D 6、A 7、D 8、A 9、D ‎10、D 11、C 12、A.‎ ‎13、(0,2)∪(3，＋∞) 14、φ＝.‎ ‎15、a≥1或a≤－3. 16、－10)的最小正周期为π.‎ ‎(Ⅰ)求ω的值；‎ ‎(Ⅱ)求f(x)的单调递增区间．‎ 解：(Ⅰ)因为 f(x)＝2sinωxcosωx＋cos2ωx ‎＝sin2ωx＋cos2ωx＝sin(2ωx＋)，‎ 所以f(x)的最小正周期T＝＝.‎ 依题意，＝π，解得ω＝1.‎ ‎(Ⅱ)由(Ⅰ)知f(x)＝sin.‎ 函数y＝sinx的单调递增区间为 ‎[2kπ－，2kπ＋](k∈Z)．‎ 由2kπ－≤2x＋≤2kπ＋(k∈Z)，得kπ－≤x≤kπ＋(k∈Z)．‎ 所以f(x)的单调递增区间为 ‎[kπ－，kπ＋](k∈Z)．‎ ‎20、已知函数f(x)＝(k为常数，e是自然对数的底数)，曲线y＝f(x)在点(1，f(1))处的切线与x轴平行．‎ ‎(1)求k的值；‎ ‎(2)求f(x)的单调区间．‎ 解：(1)由题意得f′(x)＝.‎ 又f′(1)＝＝0，故k＝1.‎ ‎(2)由(1)知，f′(x)＝.‎ 设h(x)＝－lnx－1(x>0)，则h′(x)＝－－<0，即h(x)在 (0，＋∞)上是减函数．‎ 由h(1)＝0知，当00，从而f′(x)>0；‎ 当x>1时，h(x)<0，从而f′(x)<0.‎ 综上可知，f(x)的单调递增区间是(0,1)，单调递减区间是(1，＋∞)．‎ ‎21、设△ABC的内角A，B，C所对的边分别为a，b，c，满足＝.‎ ‎(1)求角C的大小；‎ ‎(2)设函数f(x)＝cos(2x＋C)，将f(x)的图象向右平移个单位长度后得到函数g(x)的图象，求函数g(x)在区间上的值域．‎ 解：(1)∵a，b，c是△ABC的内角A，B，C所对的三边，且＝，‎ ‎∴由正弦定理得＝，即(sinA－sinB)cosC＝cosBsinC，即sinAcosC＝sinBcosC＋cosBsinC＝sin(B＋C)．‎ ‎∵A＋B＋C＝π，∴sin(B＋C)＝sinA≠0，‎ ‎∴cosC＝1，即cosC＝.‎ ‎∵C是△ABC的内角，∴C＝.‎ ‎(2)由(1)可知f(x)＝cos，‎ g(x)＝f ‎＝cos＝cos.‎ ‎∵0≤x≤，∴－≤2x－≤，‎ 又cos＝cos＝，‎ ‎∴≤cos≤1，∴g(x)在区间上的值域为.‎ ‎22、已知a∈R，函数f(x)＝ax－lnx，x∈(0，e](其中e是自然对数的底数)．‎ ‎(1)当a＝2时，求f(x)的单调区间和极值；‎ ‎(2)求函数f(x)在区间(0，e]上的最小值．‎ 解：(1)当a＝2时，f(x)＝2x－lnx，对f(x)求导，得f′(x)＝2－＝.‎ 所以f(x)的单调递减区间是，单调递增区间是.‎ 由此可知f(x)的极小值为f＝1＋ln2，没有极大值．‎ ‎(2)记g(a)为函数f(x)在区间(0，e]上的最小值．‎ f′(x)＝a－＝.‎ 当a≤0时，f′(x)<0，所以f(x)在区间(0，e]上单调递减，则g(a)＝f(e)＝ae－1；‎ 当0时，f(x)在区间上单调递减，在上单调递增，则g(a)＝f＝1＋lna.‎ 综上所述，g(a)＝