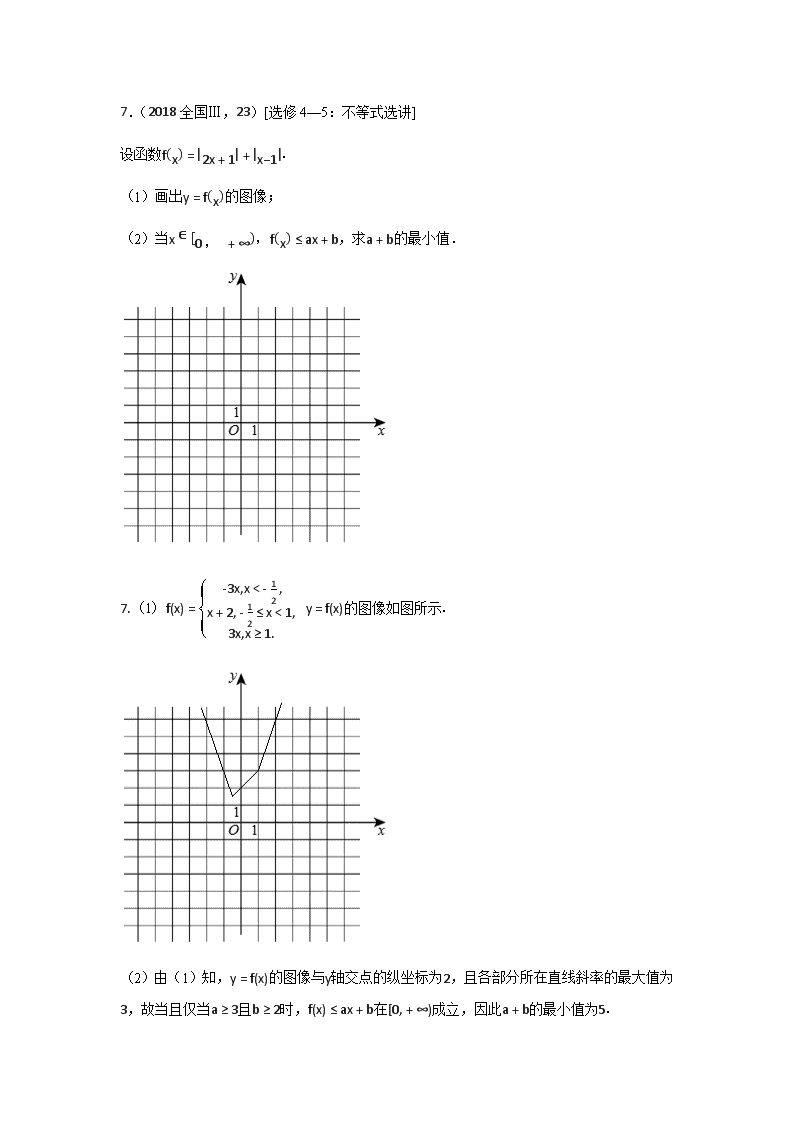2014-2018年五年真题分类选修4-5不等式选讲
选修4-5 不等式选讲
1.(2015·重庆,16)若函数f(x)=|x+1|+2|x-a|的最小值为5,则实数a=________.
1.4或-6 [由绝对值的性质知f(x)的最小值在x=-1或x=a时取得,若f(-1)=2|-1-a|=5,a=或a=-,经检验均不合适;若f(a)=5,则|x+1|=5,a=4或a=-6,经检验合题意,因此a=4或a=-6.]
2.(2014·广东,9)不等式|x-1|+|x+2|≥5的解集为________.
2.{x|x≤-3或x≥2} [原不等式等价于
或或
解得x≥2或x≤-3.故原不等式的解集为{x|x≤-3或x≥2}.]
3.(2014·湖南,13)若关于x的不等式|ax-2|<3的解集为,则a=________.
3.-3 [依题意,知a≠0.|ax-2|<3⇔-3
0时,不等式的解集为,从而有此方程组无解.
当a<0时,不等式的解集为,从而有解得a=-3.]
4.(2014·重庆,16)若不等式|2x-1|+|x+2|≥a2+a+2对任意实数x恒成立,则实数a的取值范围是________.
4. [令f(x)=|2x-1|+|x+2|,易求得f(x)min=,依题意得a2+a+2≤⇔-1≤a≤.]
5.(2018全国Ⅰ,23)[选修4–5:不等式选讲]
已知f(x)=x+1−ax−1.
(Ⅰ)当a=1时,求不等式f(x)>1的解集;
(Ⅱ)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.
5.(1)当a=1时,f(x)=|x+1|-|x-1|,即f(x)=-2,x≤-1,2x,-11的解集为{x|x>12}.
(2)当x∈(0,1)时|x+1|-|ax-1|>x成立等价于当x∈(0,1)时|ax-1|<1成立.
若a≤0,则当x∈(0,1)时|ax-1|≥1;
若a>0,|ax-1|<1的解集为02.
可得f(x)≥0的解集为{x|-2≤x≤3}.
(2)f(x)≤1等价于|x+a|+|x-2|≥4.
而|x+a|+|x-2|≥|a+2|,且当x=2时等号成立.故f(x)≤1等价于|a+2|≥4.
由|a+2|≥4可得a≤-6或a≥2,所以a的取值范围是(-∞,-6]∪[2,+∞).
7.(2018全国Ⅲ,23)[选修4—5:不等式选讲]
设函数fx=2x+1+x−1.
(1)画出y=fx的图像;
(2)当x∈0 , +∞,fx≤ax+b,求a+b的最小值.
7.(1)f(x)=-3x,x<-12,x+2,-12≤x<1,3x,x≥1. y=f(x)的图像如图所示.
(2)由(1)知,y=f(x)的图像与y轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当a≥3且b≥2时,f(x)≤ax+b在[0,+∞)成立,因此a+b的最小值为5.
8.(2018江苏,21D)[选修4—5:不等式选讲]
若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.
8.证明:由柯西不等式,得(x2+y2+z2)(12+22+22)≥(x+2y+2z)2.
因为x+2y+2z=6,所以x2+y2+z2≥4,
当且仅当x1=y2=z2时,不等式取等号,此时x=23 ,y=43 ,z=43,
所以x2+y2+z2的最小值为4.
点睛:本题考查柯西不等式等基础知识,考查推理论证能力.柯西不等式的一般形式:设a1,a2,…,an,b1,b2,…,bn为实数,则(a+a+…+a)(b+b+…+b)≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0或存在一个数k,使ai=kbi(i=1,2,…,n)时,等号成立.
9.(2017•新课标Ⅰ,23)已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.
9.(1)解:当a=1时,f(x)=﹣x2+x+4,是开口向下,对称轴为x= 的二次函数,
g(x)=|x+1|+|x﹣1|= ,
当x∈(1,+∞)时,令﹣x2+x+4=2x,解得x= ,g(x)在(1,+∞)上单调递增,f(x)在(1,+∞)上单调递减,∴此时f(x)≥g(x)的解集为(1, ];
当x∈[﹣1,1]时,g(x)=2,f(x)≥f(﹣1)=2.
当x∈(﹣∞,﹣1)时,g(x)单调递减,f(x)单调递增,且g(﹣1)=f(﹣1)=2.
综上所述,f(x)≥g(x)的解集为[﹣1, ];
(2)依题意得:﹣x2+ax+4≥2在[﹣1,1]恒成立,即x2﹣ax﹣2≤0在[﹣1,1]恒成立,则只需 ,解得﹣1≤a≤1,
故a的取值范围是[﹣1,1].
10.(2017•新课标Ⅱ,23)已知a>0,b>0,a3+b3=2,证明:
(Ⅰ)(a+b)(a5+b5)≥4;
(Ⅱ)a+b≤2.
10.证明:(Ⅰ)由柯西不等式得:(a+b)(a5+b5)≥( + )2=(a3+b3)2≥4,
当且仅当 = ,即a=b=1时取等号,
(Ⅱ)∵a3+b3=2,
∴(a+b)(a2﹣ab+b2)=2,
∴(a+b)[(a+b)2﹣3ab]=2,
∴(a+b)3﹣3ab(a+b)=2,
∴ =ab,
由均值不等式可得: =ab≤( )2 ,
∴(a+b)3﹣2≤ ,
∴ (a+b)3≤2,
∴a+b≤2,当且仅当a=b=1时等号成立.
11.(2017•新课标Ⅲ,23)已知函数f(x)=|x+1|﹣|x﹣2|.
(Ⅰ)求不等式f(x)≥1的解集;
(Ⅱ)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
11.(Ⅰ)∵f(x)=|x+1|﹣|x﹣2|= ,f(x)≥1,
∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(Ⅱ)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,
即m≤[f(x)﹣x2+x]max , 设g(x)=f(x)﹣x2+x.
由(1)知,g(x)= ,
当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x= >﹣1,
∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;
当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x= ∈(﹣1,2),
∴g(x)≤g( )=﹣ + ﹣1= ;
当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x= <2,
∴g(x)≤g(2)=﹣4+2=3=1;
综上,g(x)max= ,
∴m的取值范围为(﹣∞, ].
12.(2017•江苏,21D)已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明ac+bd≤8.
12. 证明:∵a2+b2=4,c2+d2=16,
令a=2cosα,b=2sinα,c=4cosβ,d=4sinβ.
∴ac+bd=8(cosαcosβ+sinαsinβ)=8cos(α﹣β)≤8.当且仅当cos(α﹣β)=1时取等号.
因此ac+bd≤8.
13.(2016·全国Ⅰ,24)已知函数f(x)=|x+1|-|2x-3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
13.解(1)f(x)=y=f(x)的图象如图所示.
(2)当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=或x=5,
故f(x)>1的解集为{x|11的解集为.
14.(2016·全国Ⅲ,24)已知函数f(x)=|2x-a|+a.
(1)当a=2时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x-1|.当x∈R时,f(x)+g(x)≥3,求a的取值范围.
14.解 (1)当a=2时,f(x)=|2x-2|+2.解不等式|2x-2|+2≤6得-1≤x≤3.
因此f(x)≤6的解集为{x|-1≤x≤3}.
(2)当x∈R时,f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,
所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3.①
当a≤1时,①等价于1-a+a≥3,无解.
当a>1时,①等价于a-1+a≥3,解得a≥2.
所以a的取值范围是[2,+∞).
15.(2016·全国Ⅱ,24)已知函数f(x)=+,M为不等式f(x)<2的解集.
(1)求M;
(2)证明:当a,b∈M时,|a+b|<|1+ab|.
15.(1)解 f(x)=
当x≤-时,由f(x)<2得-2x<2,解得x>-1,所以,-10.
(1)当a=1时,求不等式f(x)>1的解集;
(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
17.解 (1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-10,解得0,解得1≤x<2.
所以f(x)>1的解集为.
(2)由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),
△ABC的面积为(a+1)2.由题设得(a+1)2>6,故a>2.所以a的取值范围为(2,+∞).
18.(2015·新课标全国Ⅱ,24)设a、b、c、d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则+>+;
(2)+>+是|a-b|<|c-d|的充要条件.
18.证明 (1)因为(+)2=a+b+2,(+)2=c+d+2,
由题设a+b=c+d,ab>cd得(+)2>(+)2.因此+>+.
(2)①若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd.
因为a+b=c+d,所以ab>cd.由(1)得+>+.
②若+>+,则(+)2>(+)2,即a+b+2>c+d+2.
因为a+b=c+d,所以ab>cd,于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.
因此|a-b|<|c-d|.综上,+>+是|a-b|<|c-d|的充要条件.
19.(2014·新课标全国Ⅱ,24)设函数f(x)=|x+|+|x-a|(a>0).
(1)证明:f(x)≥2;
(2)若f(3)<5,求a的取值范围.
19.(1)证明 由a>0,有f(x)=|x+|+|x-a|≥|x+-(x-a)|=+a≥2.所以f(x)≥2.
(2)解 f(3)=|3+|+|3-a|.当a>3时,f(3)=a+,由f(3)<5得3
查看更多