- 2021-06-24 发布 |
- 37.5 KB |
- 2页

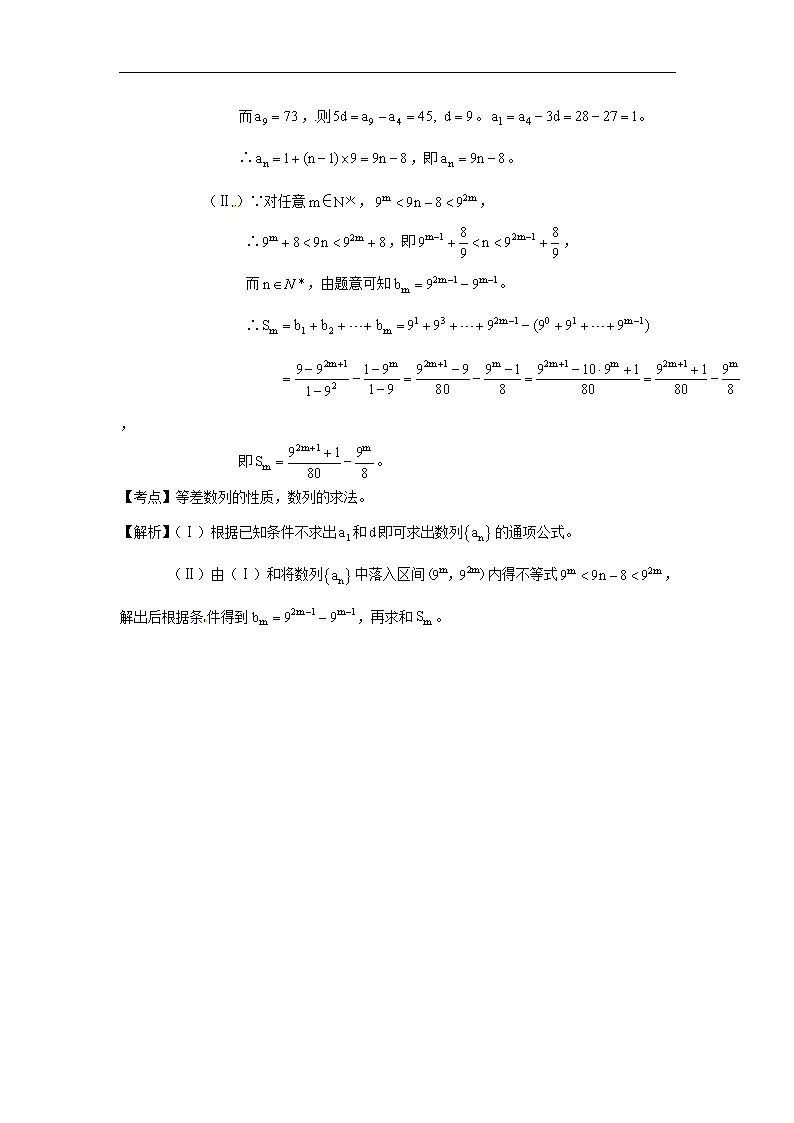
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
备战2014高考数学 高频考点归类分析(真题为例):裂项求和法的运用
裂项求和法的运用 裂项求和法是把一个数列分成几个可直接求和的数列(等差、等比数列),适用于其中{ }是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等。 典型例题: 例1. (2012年全国大纲卷理5分)已知等差数列的前项和为,则数列的前100项和为【 】[来源:Z+xx+k.Com] A. B. C. D. 【答案】A。 【考点】等差数列的通项公式和前项和公式的运用,裂项求和的综合运用。[来源:Z。xx。k.Com] 【解析】通过已知,列式求解,得到公差与首项,从而得的通项公式,进一步裂项求和: 设等差数列的公差为,则由可得[来源:学科网ZXXK][来源:学科网ZXXK] 。 ∴。 ∴。故选A。 例2. (2012年山东省理12分)在等差数列中,。 (Ⅰ)求数列的通项公式; (Ⅱ)对任意m∈N﹡,将数列中落入区间内的项的个数记为,求数列的前m项和。 【答案】解:(Ⅰ)由可得。 而,则。。 ∴,即。 (Ⅱ)∵对任意m∈N﹡,, ∴,即, 而,由题意可知。 ∴ , 即。 【考点】等差数列的性质,数列的求法。 【解析】(Ⅰ)根据已知条件不求出和即可求出数列的通项公式。[来源:学*科*网Z*X*X*K] (Ⅱ)由(Ⅰ)和将数列中落入区间内得不等式,解出后根据条件得到,再求和。查看更多