2018-2019学年安徽省亳州市第二中学高二下学期期末数学(文)试题 解析版
绝密★启用前
安徽省亳州市第二中学2018-2019学年高二下学期期末数学(文)试题
评卷人
得分
一、单选题
1.已知集合A={x|–1
1},则A∪B=
A.(–1,1) B.(1,2) C.(–1,+∞) D.(1,+∞)
【答案】C
【解析】
【分析】
根据并集的求法直接求出结果.
【详解】
∵ ,
∴ ,
故选C.
【点睛】
考查并集的求法,属于基础题.
2.下列函数中,在区间(0,+)上单调递增的是
A. B.y= C. D.
【答案】A
【解析】
【分析】
由题意结合函数的解析式考查函数的单调性即可.
【详解】
函数,
在区间 上单调递减,
函数 在区间上单调递增,故选A.
【点睛】
本题考查简单的指数函数、对数函数、幂函数的单调性,注重对重要知识、基础知识的考查,蕴含数形结合思想,属于容易题.
3.设,则“”是“”的
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】B
【解析】
【分析】
求出的解集,根据两解集的包含关系确定.
【详解】
等价于,故推不出;
由能推出。
故“”是“”的必要不充分条件。
故选B。
【点睛】
充要条件的三种判断方法:
(1)定义法:根据p⇒q,q⇒p进行判断;
(2)集合法:根据由p,q成立的对象构成的集合之间的包含关系进行判断;
(3)等价转化法:根据一个命题与其逆否命题的等价性,把要判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题.
4.下列函数中,与函数有相同定义域的是
A. B. C. D.
【答案】A
【解析】
试题分析:的定义域为,的定义域为选A.
考点:函数的定义域.
5.已知命题;命题若,则,下列命题为假命题的是( )
A. B. C. D.
【答案】C
【解析】
分析:根据给定的命题,判定命题为真命题,则为假命题,为假命题,则为真命题,利用真值表即可判定复合命题的真假,得到解答.
详解:由命题,所以为真命题,则为假命题;
又由命题若,则,则,所以为假命题,则为真命题,
根据复合命题的真值表可知,命题为假命题,故选C.
点睛:本题主要考查了命题的真假判定和复合命题的真值表的应用,其中正确判定命题的真假是解答的关键,着重考查了推理与运算能力.
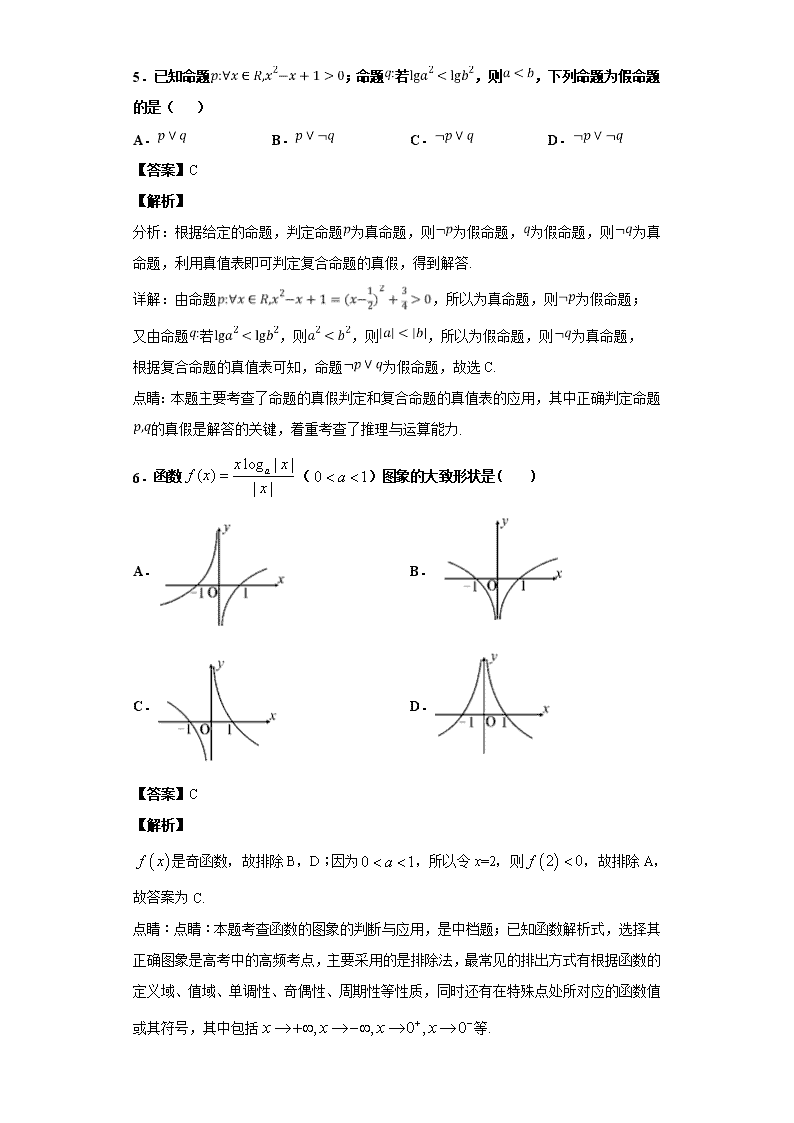
6.函数()图象的大致形状是( )
A. B.
C. D.
【答案】C
【解析】
是奇函数,故排除B,D;因为,所以令x=2,则,故排除A,故答案为C.
点睛:点睛:本题考查函数的图象的判断与应用,是中档题;已知函数解析式,选择其正确图象是高考中的高频考点,主要采用的是排除法,最常见的排出方式有根据函数的定义域、值域、单调性、奇偶性、周期性等性质,同时还有在特殊点处所对应的函数值或其符号,其中包括等.
7.已知函数,则其单调增区间是( )
A. B. C. D.
【答案】D
【解析】
,定义域为
令
解得
故函数单调增区间是
故选
8.已知在上是偶函数,且满足,当时,,则( )
A.8 B.2 C. D.50
【答案】B
【解析】
【分析】
利用函数的周期性以及函数的解析式,转化求解即可.
【详解】
在R上是偶函数,且满足,故周期为3
当时,,
则.
故选:B.
【点睛】
本题考查函数的周期性以及函数的奇偶性的应用,利用函数的解析式求解函数值,考查计算能力.
9. 在下列那个区间必有零点( )
A. B. C. D.
【答案】C
【解析】
【分析】
利用零点存在定理判断即可.
【详解】
,,,,
故选C.
【点睛】
一般地,如果在区间上,的图像是连续不间断的且,那么在内至少存在一个零点.进一步地,如果要考虑在上零点的个数,那么还需要考虑函数的单调性.
10.已知是R上的增函数,那么实数的取值范围是( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据分段函数在R上是增函数,得到每段上为增,且左边低于右边,列式取交集即可。
【详解】
解:由题意知是R上的增函数,所以
解得 ,故答案为D.
【点睛】
本题考查分段函数的单调性,当分段函数为增函数时,需满足左增右增上台阶,且第三个式子是易错点要有等号。
11.设是定义域为的偶函数,且在单调递减,则( )
A.
B.
C.
D.
【答案】C
【解析】
【分析】
由已知函数为偶函数,把,转化为同一个单调区间上,再比较大小.
【详解】
是R的偶函数,.
,
又在(0,+∞)单调递减,
∴,
,故选C.
【点睛】
本题主要考查函数的奇偶性、单调性,解题关键在于利用中间量大小比较同一区间的取值.
12.已知为上的可导函数,且有,则对于任意的,当时,有( )
A. B.
C. D.
【答案】C
【解析】
【分析】
把,通分即可构造新函数 ,并可得到的单调性,借助单调性比较大小得答案。
【详解】
解:由题意知为上的可导函数,且有,
所以,令 ,则 ,
则当 时,,,
当 时,,,
因为,当, ,即,
故答案选C。
【点睛】
本题考查导数小题中的构造函数,一般方法是应用题目中给的含有导数的式子,和要求的式子猜测出需构造的函数,利用新函数的单调性求解答案。
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人
得分
二、填空题
13.已知函数,则=_______
【答案】
【解析】
,故填2.
14.若命题“存在实数,使得”是假命题,则实数的取值为______
【答案】
【解析】
【分析】
根据命题与特称命题的否定真假不一致原则,可转化为求m的最值;根据导数判断单调性,进而求得m的取值范围。
【详解】
因为命题“存在实数x0∈[1,2],使得ex+x2+3-m<0”是假命题
所以命题的否定形式为“对于任意实数x0∈[1,2],使得ex+x2+3-m0”恒成立是真命题
由ex+x2+3-m0可得 在[1,2]上恒成立
设
在[1,2]上大于0恒成立,
所以在[1,2]为单调递增函数
所以
所以
即m的取值范围为
【点睛】
本题考查了特称命题的否定形式和恒成立问题,导数在研究最值问题中的应用,属于中档题。
15.曲线处的切线方程为__________.
【答案】
【解析】
【分析】
欲求出在处的切线的方程,只须求出其斜率即可,故先利用导数求出在处的导函数值,再结合导数的几何意义即可求出切线的斜率,从而解决问题。
【详解】
因为,所以,时,,
所以曲线在点处的切线的斜率为,
所以曲线在点处的切线的方程为,
故答案为。
【点睛】
本题主要考查利用导数研究曲线上某点切线方程、直线方程的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于基础题.
16.定义在上的函数满足,且,则=__________。
【答案】-1
【解析】
【分析】
由题目中的条件得的对称轴,再根据知是奇函数,推出的周期,再把利用周期导到已知条件上去。
【详解】
解:由题意知定义在上的函数满足,得是奇函数,所以,即,赋值得,故,得周期是8,所以
【点睛】
本题考查函数奇偶性,对称性以及推出隐含的周期性,再利用周期性把要求和已知联系起来。关于推周期有以下结论:
(1)如果函数f(x)在定义域内有两条对称轴x=a,x=b(a<b),则函数f(x)是周期函数,且周期T=2(b-a)(不一定是最小正周期,下同。)
(2)如果函数f(x)在定义域内有两个对称中心A(a,0),B(b,0) (a<b),则函数f(x)是周期函数,且周期T=2(b-a)
(3)如果函数f(x)在定义域内有一条对称轴x=a和一个对称中心B(b,0) (a≠b),则函数f(x)是周期函数,且周期T=4(b-a)
评卷人
得分
三、解答题
17.已知
(1)若,且为真,求实数的取值范围;
(2)若是充分不必要条件,求实数的取值范围
【答案】(1);(2)
【解析】
【分析】
(1)解不等求得p,根据m的值求得q;根据p∧ q为真可知p、q同时为真,可求得x的取值范围。
(2)先求得q。根据p是q的充分不必要条件,得到不等式组,解不等式组即可得到m的取值范围。
【详解】
(1)由x2-6x+5≤0,得1≤x≤5,∴p:1≤x≤5.
当m=2时,q:-1≤x≤3.
若p∧q为真,p,q同时为真命题,
则即1≤x≤3.
∴实数x的取值范围为[1,3].
(2)由x2-2x+1-m2≤0,得q:1-m≤x≤1+m.
∵p是q的充分不必要条件,
∴解得m≥4.
∴实数m的取值范围为[4,+∞).
【点睛】
本题考查了复合命题的简单应用,充分必要条件的关系,属于基础题。
18.在直角坐标系中,曲线的参数方程为 (其中参数).
(1)以坐标原点为极点,轴非负半轴为极轴建立极坐标系,求曲线的极坐标方程;
(2)直线的参数方程为 (其中参数,是常数),直线与曲线交于两点,且,求直线的斜率.
【答案】(1)(2)
【解析】
【分析】
(1) 先把参数方程化普通方程,再由普通方程化极坐标方程。
(2) 本题已知直线和圆相交的弦长,设出直线普通方程,利用垂径定理表示出半弦长、半径、圆心距关系,求出直线的斜率。
【详解】
解: (1)
的普通方程
的极坐标方程
(2)
直线的普通方程
由(1)知:圆心,,
,
【点睛】
本题考查圆的参数方程,普通方程和极坐标方程的互化,以及直线与圆相交的弦长问题。
19.设函数在及时取得极值.
(1)求 的值;
(2)若对于任意的,都有成立,求的取值范围.
【答案】(Ⅰ),.(Ⅱ)。
【解析】
【分析】
(Ⅰ)求出,利用,列方程即可得结果;(Ⅱ)由(Ⅰ)可知,,利用导数研究函数的单调性,求得函数的极值,与区间端点函数值比较大小可得的最大值为,由解不等式即可得结果.
【详解】
(Ⅰ),
因为函数在及取得极值,则有,.
即
解得,.
(Ⅱ)由(Ⅰ)可知,,
.
当时,;当时,;
当时,.所以,当时,取得极大值,又,.则当时,
的最大值为.因为对于任意的,有恒成立,所以 ,解得 或,因此的取值范围为.
【点睛】
本题主要考查利用导数判断函数的单调性以及函数的极值与最值,属于难题.求函数极值的步骤:(1) 确定函数的定义域;(2) 求导数;(3) 解方程求出函数定义域内的所有根;(4) 列表检查在的根左右两侧值的符号,如果左正右负(左增右减),那么在处取极大值,如果左负右正(左减右增),那么在处取极小值. (5)如果只有一个极值点,则在该处即是极值也是最值;(6)如果求闭区间上的最值还需要比较端点值的函数值与极值的大小.
20.已知函数.
(1)求不等式的解集;
(2)若不等式解集非空,求实数的取值范围.
【答案】(1);(2)或
【解析】
【分析】
(1)通过对x取值的分类讨论,去掉绝对值符号,即可求得不等式f(x)≤6的解集;
(2)由题意可得|a﹣1|应大于函数f(x)=|2x+1|+|2x﹣3|的最小值,而由绝对值的意义可得f(x)的最小值为4,故有a2﹣3a>4,由此求得实数a的取值范围
【详解】
(1),
(2)因为,当且仅当时取等
故不等式解集非空,
等价于或.
【点睛】
含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.法一是运用分类讨论思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.
21.已知函数.
(1)若在上是单调函数,求的取值范围.
(2)当时,求函数的值域.
【答案】(1)或;(2)
【解析】
分析:(1)由函数的解析式可知对称轴为,则或 .
(2)由题意结合复合函数的单调性可得函数的值域是.
详解:(1) 对称轴为,
在上是单调函数或 即或 ,
(2)当时, ,
令,
, ,
而是增函数, 函数的值域是.
点睛:本题主要考查指数函数的性质,二次函数的性质,函数的单调性及其应用等知识,意在考查学生的转化能力和计算求解能力.
22.已知函数.
(1)讨论函数的单调性;
(2)若函数在定义域内恒有,求实数的取值范围;
【答案】(1)见解析(2) [0,2]
【解析】
分析:第一问对函数求导,结合函数的定义域,对的范围进行讨论,确定出函数在哪个区间上单调增,在哪个区间上单调减,最后确定出结果;第二问函数f(x)在定义域内恒有f(x)≤0,转化为函数的最大值小于等于零即可,最后转化为求函数最值问题来解决.
详解:(1)
当上递减;
当时,令,得(负根舍去).
当得,;令,得,
∴上递增,在(上递减
(2) 当,符合题意.
当时,
∴
当时,在()上递减,
且的图象在()上只有一个交点,设此交点为(),
则当x∈时,,故当时,不满足
综上,a的取值范围[0,2]
点睛:该题属于应用导数研究函数的性质的综合题,考查了含有参数的函数的单调性的讨论问题,需要对参数的范围进行讨论,第二问恒成立问题转化为最值问题来处理即可得结果.