2018年四川省资阳市高考数学二诊试卷（理科）

2018年四川省资阳市高考数学二诊试卷（理科）

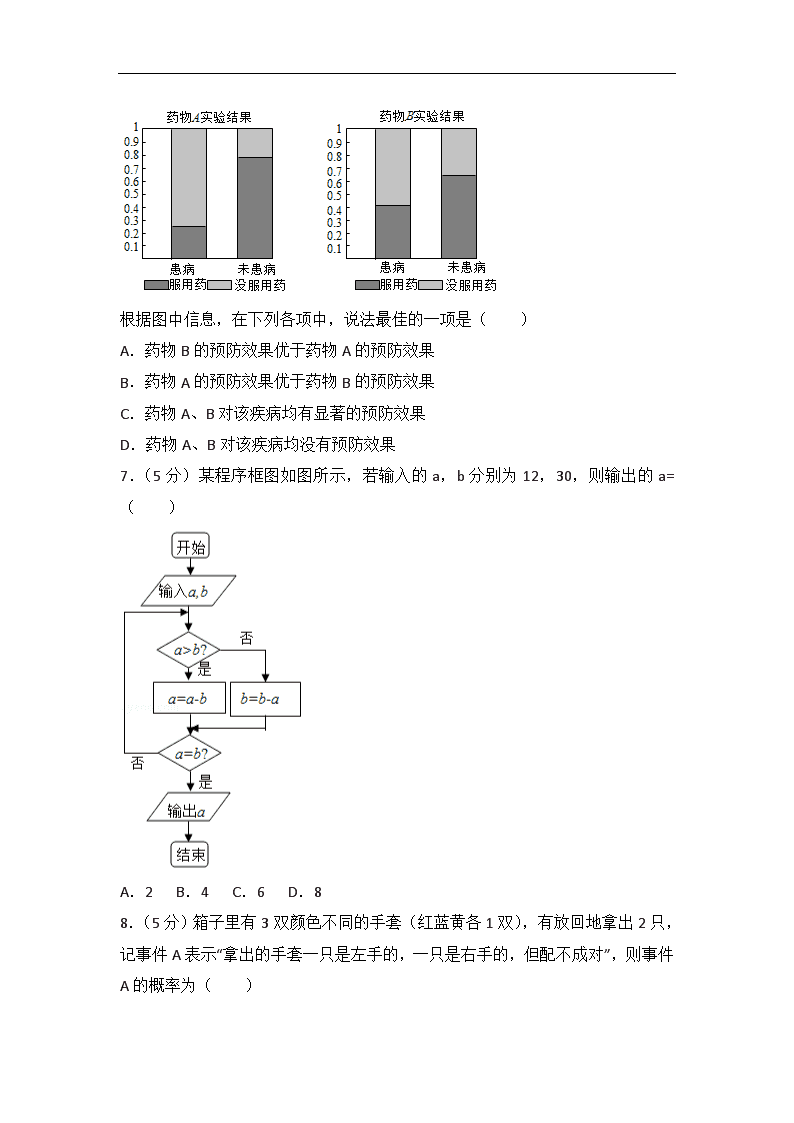
‎2018年四川省资阳市高考数学二诊试卷（理科）‎ ‎　‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）设集合A={x|x2﹣x﹣2＜0}，B={x|x2＞1}，则A∩（∁RB）=（　　）‎ A．{x|﹣2＜x＜1} B．{x|﹣2＜x≤1} C．{x|﹣1＜x≤1} D．{x|﹣1＜x＜1}‎ ‎2．（5分）复数z满足z（1﹣2i）=3+2i，则=（　　）‎ A． B． C． D．‎ ‎3．（5分）已知命题p：∃x0∈R，x0﹣2＜lgx0；命题q：∀x∈（0，1），，则（　　）‎ A．“p∨q”是假命题 B．“p∧q”是真命题 C．“p∧（¬q）”是真命题 D．“p∨（¬q）”是假命题 ‎4．（5分）一个几何体的三视图如图所示，则该几何体的体积为（　　）‎ A． B． C． D．π ‎5．（5分）设实数x，y满足，则x﹣2y的最小值为（　　）‎ A．﹣5 B．﹣4 C．﹣3 D．﹣1‎ ‎6．（5分）为考察A、B两种药物预防某疾病的效果，进行动物试验，分别得到如下等高条形图：‎ 根据图中信息，在下列各项中，说法最佳的一项是（　　）‎ A．药物B的预防效果优于药物A的预防效果 B．药物A的预防效果优于药物B的预防效果 C．药物A、B对该疾病均有显著的预防效果 D．药物A、B对该疾病均没有预防效果 ‎7．（5分）某程序框图如图所示，若输入的a，b分别为12，30，则输出的a=（　　）‎ A．2 B．4 C．6 D．8‎ ‎8．（5分）箱子里有3双颜色不同的手套（红蓝黄各1双），有放回地拿出2只，记事件A表示“拿出的手套一只是左手的，一只是右手的，但配不成对”，则事件A的概率为（　　）‎ A． B． C． D．‎ ‎9．（5分）在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=120°，AB=AC=1，，则直线PA与平面PBC所成角的正弦值为（　　）‎ A． B． C． D．‎ ‎10．（5分）过抛物线C1：x2=4y焦点的直线l交C1于M，N两点，若C1在点M，N处的切线分别与双曲线C2：=1（a＞0，b＞0）的渐近线平行，则双曲线C2的离心率为（　　）‎ A． B． C． D．‎ ‎11．（5分）边长为8的等边△ABC所在平面内一点O，满足=，若M为△ABC边上的点，点P满足|，则|MP|的最大值为（　　）‎ A． B． C． D．‎ ‎12．（5分）已知函数f（x）=cos（ωx+φ）（其中ω≠0）的一个对称中心的坐标为，一条对称轴方程为．有以下3个结论：‎ ‎①函数f（x）的周期可以为；‎ ‎②函数f（x）可以为偶函数，也可以为奇函数；‎ ‎③若，则ω可取的最小正数为10．‎ 其中正确结论的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．（5分）二项式的展开式中x5的系数为　 　．‎ ‎14．（5分）由曲线y=x2和直线y=1所围成的封闭图形面积为　 　．‎ ‎15．（5分）如图，为测量竖直旗杆CD高度，在旗杆底部C所在水平地面上选取相距4‎ m的两点A，B，在A处测得旗杆底部C在西偏北20°的方向上，旗杆顶部D的仰角为60°；在B处测得旗杆底部C在东偏北10°方向上，旗杆顶部D的仰角为45°，则旗杆CD高度为　 　m．‎ ‎16．（5分）已知函数如果使等式成立的实数x1，x3分别都有3个，而使该等式成立的实数x2仅有2个，则的取值范围是　 　．‎ ‎　‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，且Sn=2an﹣2．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若bn=anlog2an，Tn=b1+b2+…+bn，求成立的正整数n的最小值．‎ ‎18．（12分）某地区某农产品近几年的产量统计如表：‎ 年 份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 年份代码t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 年产量y（万吨）‎ ‎6.6‎ ‎6.7‎ ‎7‎ ‎7.1‎ ‎7.2‎ ‎7.4‎ ‎（1）根据表中数据，建立y关于t的线性回归方程；‎ ‎（2）若近几年该农产品每千克的价格v（单位：元）与年产量y满足的函数关系式为v=4.5﹣0.3y，且每年该农产品都能售完．‎ ‎①根据（1）中所建立的回归方程预测该地区2018（t=7）年该农产品的产量；‎ ‎②当t（1≤t≤7）为何值时，销售额S最大？‎ 附：对于一组数据（t1，y1），（t2，y2），…，（tn，yn），其回归直线的斜率和截距的最小二乘估计分别为：，．‎ ‎19．（12分）如图，在三棱柱ABC﹣A1B1C1中，侧面ACC1A1⊥底面ABC，AA1=A1C=AC，AB=BC，AB⊥BC，E，F分别为AC，B1C1的中点．‎ ‎（1）求证：直线EF∥平面ABB1A1；‎ ‎（2）求二面角A1﹣BC﹣B1的余弦值．‎ ‎20．（12分）已知椭圆C：的离心率，且过点．‎ ‎（1）求椭圆C的方程；‎ ‎（2）过P作两条直线l1，l2与圆相切且分别交椭圆于M，N两点．‎ ‎①求证：直线MN的斜率为定值；‎ ‎②求△MON面积的最大值（其中O为坐标原点）．‎ ‎21．（12分）已知函数f（x）=（x＞0，a∈R）．‎ ‎（1）当时，判断函数f（x）的单调性；‎ ‎（2）当f（x）有两个极值点时，‎ ‎①求a的取值范围；‎ ‎②若f（x）的极大值小于整数m，求m的最小值．‎ ‎　‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）在直角坐标系xOy中，直线l的参数方程为（其中t为参数），在以原点O为极点，以x轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=4sinθ．‎ ‎（1）求直线l的普通方程及曲线C的直角坐标方程；‎ ‎（2）设M是曲线C上的一动点，OM的中点为P，求点P到直线l的最小值．‎ ‎　‎ ‎[选修4-5：不等式选讲]（10分）‎ ‎23．已知函数f（x）=|2x+a|+|x﹣2|（其中a∈R）．‎ ‎（1）当a=﹣4时，求不等式f（x）≥6的解集；‎ ‎（2）若关于x的不等式f（x）≥3a2﹣|2﹣x|恒成立，求a的取值范围．‎ ‎　‎ ‎2018年四川省资阳市高考数学二诊试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）设集合A={x|x2﹣x﹣2＜0}，B={x|x2＞1}，则A∩（∁RB）=（　　）‎ A．{x|﹣2＜x＜1} B．{x|﹣2＜x≤1} C．{x|﹣1＜x≤1} D．{x|﹣1＜x＜1}‎ ‎【解答】解：A={x|x2﹣x﹣2＜0}={x|﹣1＜x＜2}，B={x|x2＞1}={x|x＞1或x＜﹣1}，‎ 则∁RB={x|﹣1≤x≤1}，‎ 则A∩（∁RB）={x|﹣1＜x≤1}，‎ 故选：C ‎　‎ ‎2．（5分）复数z满足z（1﹣2i）=3+2i，则=（　　）‎ A． B． C． D．‎ ‎【解答】解：由z（1﹣2i）=3+2i，‎ 得z=，‎ ‎∴．‎ 故选：A．‎ ‎　‎ ‎3．（5分）已知命题p：∃x0∈R，x0﹣2＜lgx0；命题q：∀x∈（0，1），，则（　　）‎ A．“p∨q”是假命题 B．“p∧q”是真命题 C．“p∧（¬q）”是真命题 D．“p∨（¬q）”是假命题 ‎【解答】解：当x=1时，x﹣2=1﹣2=﹣1，lg1=0，满足x0﹣2＜lgx0，即命题p是真命题，‎ 当x＞0时，x+≥2=2，当且仅当x=，即x=1取等号，‎ ‎∵x∈（0，1），∴，成立，即q为真命题，‎ 则“p∧q”是真命题，其余为假命题，‎ 故选：B．‎ ‎　‎ ‎4．（5分）一个几何体的三视图如图所示，则该几何体的体积为（　　）‎ A． B． C． D．π ‎【解答】解：由题意可知，几何体是半圆柱，底面半圆的半径为1，圆柱的高为2，‎ 所以该几何体的体积为：V==π．‎ 故选：D．‎ ‎　‎ ‎5．（5分）设实数x，y满足，则x﹣2y的最小值为（　　）‎ A．﹣5 B．﹣4 C．﹣3 D．﹣1‎ ‎【解答】解：先根据约束条件实数x，y满足画出可行域，‎ 由，解得A（1，3）‎ 当直线z=x﹣2y过点A（1，3）时，‎ z最小是﹣5，‎ 故选：A．‎ ‎　‎ ‎6．（5分）为考察A、B两种药物预防某疾病的效果，进行动物试验，分别得到如下等高条形图：‎ 根据图中信息，在下列各项中，说法最佳的一项是（　　）‎ A．药物B的预防效果优于药物A的预防效果 B．药物A的预防效果优于药物B的预防效果 C．药物A、B对该疾病均有显著的预防效果 D．药物A、B对该疾病均没有预防效果 ‎【解答】解：由A、B两种药物预防某疾病的效果，进行动物试验，分别得到的等高条形图，知：‎ 药物A的预防效果优于药物B的预防效果．‎ 故选：B．‎ ‎　‎ ‎7．（5分）某程序框图如图所示，若输入的a，b分别为12，30，则输出的a=（　　）‎ A．2 B．4 C．6 D．8‎ ‎【解答】解：模拟程序的运行，可得 a=12，b=30，‎ a＜b，则b变为30﹣12=18，‎ 不满足条件a=b，由a＜b，则b变为18﹣12=6，‎ 不满足条件a=b，由a＞b，则a变为12﹣6=6，‎ 由a=b=6，‎ 则输出的a=6．‎ 故选：C．‎ ‎　‎ ‎8．（5分）箱子里有3双颜色不同的手套（红蓝黄各1双），有放回地拿出2只，记事件A表示“拿出的手套一只是左手的，一只是右手的，但配不成对”，则事件A的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：分别设3双手套为：a1a2；b1b2；c1c2．a1，b1，c1‎ 分别代表左手手套，a2，b2，c2分别代表右手手套．‎ 从箱子里的3双不同的手套中，随机拿出2只，所有的基本事件是：‎ n=6×6=36，共36个基本事件．‎ 事件A包含：（a1，b2），（b2，a1），（a1，c2），（c2，a1），（a2，b1），（b1，a2），‎ ‎（a2，c1），（c1，a2），（b1，c2），（c2，b1），（b2，c1），（c1，b2），12个基本事件，‎ 故事件A的概率为P（A）==．‎ 故选：B．‎ ‎　‎ ‎9．（5分）在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=120°，AB=AC=1，，则直线PA与平面PBC所成角的正弦值为（　　）‎ A． B． C． D．‎ ‎【解答】解：∵PA⊥底面ABC，AB=AC=1，，∴△PAB≌△PAC，PB=PC．‎ 取BC中点D，连接AD，PD，∴PD⊥BC，AD⊥BC，∴BC⊥面PAD．‎ ‎∴面PAD⊥面PBC，‎ 过A作AO⊥PD于O，可得AO⊥面PBC，‎ ‎∴∠APD就是直线PA与平面PBC所成角，‎ 在Rt△PAD中，AD=，PA=，PD=，‎ sin．‎ 故选：D ‎　‎ ‎10．（5分）过抛物线C1：x2=4y焦点的直线l交C1于M，N两点，若C1‎ 在点M，N处的切线分别与双曲线C2：=1（a＞0，b＞0）的渐近线平行，则双曲线C2的离心率为（　　）‎ A． B． C． D．‎ ‎【解答】解：由双曲线C2：=1（a＞0，b＞0）的渐近线方程 y=±x，‎ 可得两条切线的斜率分别为±，‎ 则两条切线关于y轴对称，‎ 由y=x2的导数为y′=x，‎ 则过抛物线C1：x2=4y焦点（0，1）的直线为y=1，‎ 可得切点为（﹣2，1）和（2，1），‎ 则切线的斜率为±1，‎ 即a=b，c==a，‎ 则e==．‎ 故选C．‎ ‎　‎ ‎11．（5分）边长为8的等边△ABC所在平面内一点O，满足=，若M为△ABC边上的点，点P满足|，则|MP|的最大值为（　　）‎ A． B． C． D．‎ ‎【解答】解：如图，由=，得，‎ 即，取AB中点G，AC中点H，连接GH，‎ 则，即，‎ 取GH中点K，延长KG到O，使KG=GO，则O为所求点，‎ ‎∵点P满足|，M为△ABC边上的点，‎ ‎∴当M与A重合时，|MP|有最大值为|OA|+|OP|，‎ 而|OA|=，‎ ‎∴|MP|的最大值为，‎ 故选：D．‎ ‎　‎ ‎12．（5分）已知函数f（x）=cos（ωx+φ）（其中ω≠0）的一个对称中心的坐标为，一条对称轴方程为．有以下3个结论：‎ ‎①函数f（x）的周期可以为；‎ ‎②函数f（x）可以为偶函数，也可以为奇函数；‎ ‎③若，则ω可取的最小正数为10．‎ 其中正确结论的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：对于①，∵函数f（x）=cos（ωx+φ）（其中ω≠0）的一个对称中心的坐标为，一条对称轴方程为．‎ ‎∴，T=，故①正确；‎ 对于②，如果函数f（x（为奇函数，则有f（0）=0，可得φ=kπ+，此时f（x）=f（x）=cos（ωx+k）=±sinωx，函数f（x）不可以为偶函数，故错；‎ 对于③，∵函数f（x）=cos（ωx+）的一条对称轴为x=，‎ ‎∴ω•+=kπ，解得ω=3k﹣2，k∈Z；‎ 又∵函数f（x）一个对称中心为点（，0），∴ω•+=mπ+，解得ω=12m﹣2，m∈Z；‎ 由ω＞0可知当m=0，k=4时，ω取最小值10．故正确；‎ ‎ 故选：C ‎　‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．（5分）二项式的展开式中x5的系数为　35　．‎ ‎【解答】解：二项式展开式的通项公式为 Tr+1=•（x3）7﹣r•=•x21﹣4r，‎ 令21﹣4r=5，解得r=4；‎ ‎∴展开式中x5的系数为 ‎=35．‎ 故答案为：35．‎ ‎　‎ ‎14．（5分）由曲线y=x2和直线y=1所围成的封闭图形面积为　　．‎ ‎【解答】解：联立方程组，解得或，‎ ‎∴曲线y=x2与直线y=x围成的封闭图形的面积为S==．‎ 故答案为：‎ ‎　‎ ‎15．（5分）如图，为测量竖直旗杆CD高度，在旗杆底部C所在水平地面上选取相距4m的两点A，B，在A处测得旗杆底部C在西偏北20°的方向上，旗杆顶部D的仰角为60°；在B处测得旗杆底部C在东偏北10°方向上，旗杆顶部D的仰角为45°，则旗杆CD高度为　12　m．‎ ‎【解答】解：如图所示，设CD=x 在Rt△BCD，∠CBD=45°，‎ ‎∴BC=x，‎ 在Rt△ACD，∠CAD=60°，‎ ‎∴AC==，‎ 在△ABC中，∠CAB=20°，∠CBA=10°，AB=4‎ ‎∴∠ACB=180°﹣20°﹣10°=150°，‎ 由余弦定理可得AB2=AC2+BC2﹣2AC•BC•cos150°，‎ 即（4）2=x2+x2+2••x•=x2，‎ 解得x=12，‎ 故答案为：12．‎ ‎　‎ ‎16．（5分）已知函数如果使等式 成立的实数x1，x3分别都有3个，而使该等式成立的实数x2仅有2个，则的取值范围是　（1，3]　．‎ ‎【解答】解：当﹣3≤x≤0时，y=﹣x（x+2）2的导数为y′=﹣（x+2）（3x+2），‎ 可得﹣2＜x＜﹣时，函数递增；﹣3＜x＜﹣2，﹣＜x＜0，函数递减；‎ 当x＞0时，y=2ex（4﹣x）﹣8的导数为y′=2ex（3﹣x），‎ 当x＞3时，函数递减；0＜x＜3时，函数递增，‎ x=3时，y=2e3﹣8，‎ 作出函数f（x）的图象，‎ 等式=k表示点（﹣4，0），（﹣2，0），（﹣，0）与 f（x）图象上的点的斜率相等，‎ 由（﹣3，3）与（﹣4，0）的连线与f（x）有3个交点，‎ 且斜率为3，则k的最大值为3；‎ 由题意可得，过（﹣2，0）的直线与f（x）的图象相切，转到斜率为3的时候，‎ 实数x2仅有2个，‎ 设切点为（m，n），（﹣2＜m＜0），‎ 求得切线的斜率为﹣（m+2）（3m+2）=，‎ 解得m=﹣1，‎ 此时切线的斜率为1，‎ 则k的范围是（1，3]．‎ 故答案为：（1，3]．‎ ‎　‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，且Sn=2an﹣2．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）若bn=anlog2an，Tn=b1+b2+…+bn，求成立的正整数n的最小值．‎ ‎【解答】（12分）解：（1）当n=1时，a1=2a1﹣2，解得a1=2，‎ 当n≥2时，Sn=2an﹣2，Sn﹣1=2an﹣1﹣2．则an=2an﹣2an﹣1，所以an=2an﹣1，‎ 所以{an}是以2为首项，2为公比的等比数列．‎ 故．（4分）‎ ‎（2），‎ 则①‎ ‎②‎ ‎①﹣②得：==2n+1﹣n•2n+1﹣2．‎ 所以．‎ 由得2n+1＞52．‎ 由于n≤4时，2n+1≤25=32＜52；n≥5时，2n+1≥26=64＞52．‎ 故使成立的正整数n的最小值为5．（12分）‎ ‎　‎ ‎18．（12分）某地区某农产品近几年的产量统计如表：‎ 年 份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 年份代码t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 年产量y（万吨）‎ ‎6.6‎ ‎6.7‎ ‎7‎ ‎7.1‎ ‎7.2‎ ‎7.4‎ ‎（1）根据表中数据，建立y关于t的线性回归方程；‎ ‎（2）若近几年该农产品每千克的价格v（单位：元）与年产量y满足的函数关系式为v=4.5﹣0.3y，且每年该农产品都能售完．‎ ‎①根据（1）中所建立的回归方程预测该地区2018（t=7）年该农产品的产量；‎ ‎②当t（1≤t≤7）为何值时，销售额S最大？‎ 附：对于一组数据（t1，y1），（t2，y2），…，（tn，yn），其回归直线的斜率和截距的最小二乘估计分别为：，．‎ ‎【解答】解：（1）由题意可知：，，‎ ‎=（﹣2.5）×（﹣0.4）+（﹣1.5）×（﹣0.3）+0+0.5×0.1+1.5×0.2+2.5×0.4=2.8，‎ ‎=（﹣2.5）2+（﹣1.5）2+（﹣0.5）2+0.52+1.52+2.52=17.5．‎ ‎，，又，得，‎ ‎∴y关于t的线性回归方程为．（6分）‎ ‎（2）①由（1）知，当t=7时，，‎ 即2018年该农产品的产量为7.56万吨．‎ ‎②当年产量为y时，销售额S=（4.5﹣0.3y）y×103=（﹣0.3y2+4.5y）×103（万元），‎ 当y=7.5时，函数S取得最大值，又因y∈{6.6，6.7，7，7.1，7.2，7.4，7.56}，‎ 计算得当y=7.56，即t=7时，即2018年销售额最大．（12分）‎ ‎　‎ ‎19．（12分）如图，在三棱柱ABC﹣A1B1C1中，侧面ACC1A1⊥底面ABC，AA1=A1C=AC，AB=BC，AB⊥BC，E，F分别为AC，B1C1的中点．‎ ‎（1）求证：直线EF∥平面ABB1A1；‎ ‎（2）求二面角A1﹣BC﹣B1的余弦值．‎ ‎【解答】（12分）（1）证明：取A1C1的中点G，连接EG，FG，由于E，F分别为AC，B1C1的中点，‎ 所以FG∥A1B1．又A1B1⊂平面ABB1A1，FG⊄平面ABB1A1，所以FG∥平面ABB1A1．又AE∥A1G且AE=A1G，‎ 所以四边形AEGA1是平行四边形．‎ 则EG∥AA1．又AA1⊂平面ABB1A1，EG⊄平面ABB1A1，‎ 所以EG∥平面ABB1A1．‎ 所以平面EFG∥平面ABB1A1．又EF⊂平面EFG，‎ 所以直线EF∥平面ABB1A1．（6分）‎ ‎（2）解：令AA1=A1C=AC=2，‎ 由于E为AC中点，则A1E⊥AC，又侧面AA1C1C⊥底面ABC，交线为AC，A1E⊂平面A1AC，‎ 则A1E⊥平面ABC，连接EB，可知EB，EC，EA1两两垂直．以E为原点，分别以EB，EC，EA1所在直线为x，y，z轴，建立空间直角坐标系，‎ 则B（1，0，0），C（0，1，0），A1（0，0，），A（0，﹣1，0），．‎ 所以，，，‎ 令平面A1BC的法向量为=（x1，y1，z1），‎ 由则令，则=（，，1）．‎ 令平面B1BC的法向量为=（x2，y2，z2），‎ 由则令，则=（，，﹣1）．‎ 由cos==，故二面角A1﹣BC﹣B1的余弦值为．（12分）‎ ‎　‎ ‎20．（12分）已知椭圆C：的离心率，且过点．‎ ‎（1）求椭圆C的方程；‎ ‎（2）过P作两条直线l1，l2与圆 相切且分别交椭圆于M，N两点．‎ ‎①求证：直线MN的斜率为定值；‎ ‎②求△MON面积的最大值（其中O为坐标原点）．‎ ‎【解答】（12分）解：（1）由，设椭圆的半焦距为c，所以a=2c，‎ 因为C过点，所以，又c2+b2=a2，解得，‎ 所以椭圆方程为．（4分）‎ ‎（2）①显然两直线l1，l2的斜率存在，设为k1，k2，M（x1，y1），N（x2，y2），‎ 由于直线l1，l2与圆相切，则有k1=﹣k2，‎ 直线l1的方程为，联立方程组 消去y，得，‎ 因为P，M为直线与椭圆的交点，所以，‎ 同理，当l2与椭圆相交时，，‎ 所以，而，‎ 所以直线MN的斜率．‎ ‎②设直线MN的方程为，联立方程组，‎ 消去y得x2+mx+m2﹣3=0，‎ 所以，‎ 原点O到直线的距离，△OMN得面积为 ‎，‎ 当且仅当m2=2时取得等号．经检验，存在r（），‎ 使得过点的两条直线与圆（x﹣1）2+y2=r2相切，‎ 且与椭圆有两个交点M，N．‎ 所以△OMN面积的最大值为．（12分）‎ ‎　‎ ‎21．（12分）已知函数f（x）=（x＞0，a∈R）．‎ ‎（1）当时，判断函数f（x）的单调性；‎ ‎（2）当f（x）有两个极值点时，‎ ‎①求a的取值范围；‎ ‎②若f（x）的极大值小于整数m，求m的最小值．‎ ‎【解答】解：（1）由题f′（x）=，（x＞0）‎ 方法1：由于，﹣ex＜﹣1＜0，（﹣x2+3x﹣3）ex＜﹣，‎ 又，所以（﹣x2+3x﹣3）ex﹣a＜0，从而f'（x）＜0，‎ 于是f（x）为（0，+∞）上的减函数．（4分）‎ 方法2：令h（x）=（﹣x2+3x﹣3）ex﹣a，则h′（x）=（﹣x2+x）ex，‎ 当0＜x＜1时，h'（x）＞0，h（x）为增函数；‎ 当x＞1时，h'（x）＜0，h（x）为减函数．‎ 故h（x）在x=1时取得极大值，也即为最大值．‎ 则h（x）max=﹣e﹣a．由于，所以h（x）max=h（1）=﹣e﹣a＜0，‎ 于是f（x）为（0，+∞）上的减函数．（4分）‎ ‎（2）①令h（x）=（﹣x2+3x﹣3）ex﹣a，则h′（x）=（﹣x2+x）ex，‎ 当0＜x＜1时，h'（x）＞0，h（x）为增函数，‎ 当x＞1时，h'（x）＜0，h（x）为减函数，‎ 当x趋近于+∞时，h（x）趋近于﹣∞．‎ 由于f（x）有两个极值点，所以f'（x）=0有两不等实根，‎ 即h（x）=0有两不等实数根x1，x2（x1＜x2），‎ 则，解得﹣3＜a＜﹣e，‎ ‎②可知x1∈（0，1），由于h（1）=﹣e﹣a＞0，h（）=﹣﹣a＜﹣+3＜0，则．‎ 而f′（x2）==0，即=（#）‎ 所以g（x）极大值=f（x2）=，于是，（*）‎ 令，则（*）可变为，‎ 可得，而﹣3＜a＜﹣e，则有，‎ 下面再说明对于任意﹣3＜a＜﹣e，，f（x2）＞2．‎ 又由（#）得a=（﹣+3x2﹣3），把它代入（*）得f（x2）=（2﹣x2），‎ 所以当时，f′（x2）=（1﹣x2）＜0恒成立，‎ 故f（x2）为的减函数，所以f（x2）＞f（）=＞2，‎ 所以满足题意的整数m的最小值为3．‎ ‎　‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）在直角坐标系xOy中，直线l的参数方程为 ‎（其中t为参数），在以原点O为极点，以x轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=4sinθ．‎ ‎（1）求直线l的普通方程及曲线C的直角坐标方程；‎ ‎（2）设M是曲线C上的一动点，OM的中点为P，求点P到直线l的最小值．‎ ‎【解答】[选修4﹣4：坐标系与参数方程]（10分）‎ 解：（1）∵直线l的参数方程为（其中t为参数），‎ ‎∴消去参数t，得l的普通方程x﹣y﹣1=0．‎ ‎∵曲线C的极坐标方程为ρ=4sinθ．由ρ=4sinθ，得ρ2=4ρsinθ，‎ ‎∴曲线C的直角坐标方程为x2+y2﹣4y=0，即x2+（y﹣2）2=4．（4分）‎ ‎（2）设P（x，y），M（x0，y0），则，‎ 由于P是OM的中点，则x0=2x，y0=2y，所以（2x）2+（2y﹣2）2=4，‎ 得点P的轨迹方程为x2+（y﹣1）2=1，轨迹为以（0，1）为圆心，1为半径的圆．‎ 圆心（0，1）到直线l的距离．‎ 所以点P到直线l的最小值为．（10分）‎ ‎　‎ ‎[选修4-5：不等式选讲]（10分）‎ ‎23．已知函数f（x）=|2x+a|+|x﹣2|（其中a∈R）．‎ ‎（1）当a=﹣4时，求不等式f（x）≥6的解集；‎ ‎（2）若关于x的不等式f（x）≥3a2﹣|2﹣x|恒成立，求a的取值范围．‎ ‎【解答】[选修4﹣5：不等式选讲]（10分）‎ 解：（1）当a=﹣4时，求不等式f（x）≥6，即为|2x﹣4|+|x﹣2|≥6，‎ 所以|x﹣2|≥2，即x﹣2≤﹣2或x﹣2≥2，‎ 原不等式的解集为{x|x≤0或x≥4}．（4分）‎ ‎（2）不等式f（x）≥3a2﹣|2﹣x|即为|2x+a|+|x﹣2|≥3a2﹣|2﹣x|，‎ 即关于x的不等式|2x+a|+|4﹣2x|≥3a2恒成立．‎ 而|2x+a|+|4﹣2x|≥|a+4|，‎ 所以|a+4|≥3a2，‎ 解得a+4≥3a2或a+4≤﹣3a2，‎ 解得或a∈∅．‎ 所以a的取值范围是．（10分）‎ ‎　‎