天一大联考2020届高三阶段性测试（五） 数学（文）

天一大联考2020届高三阶段性测试（五） 数学（文）

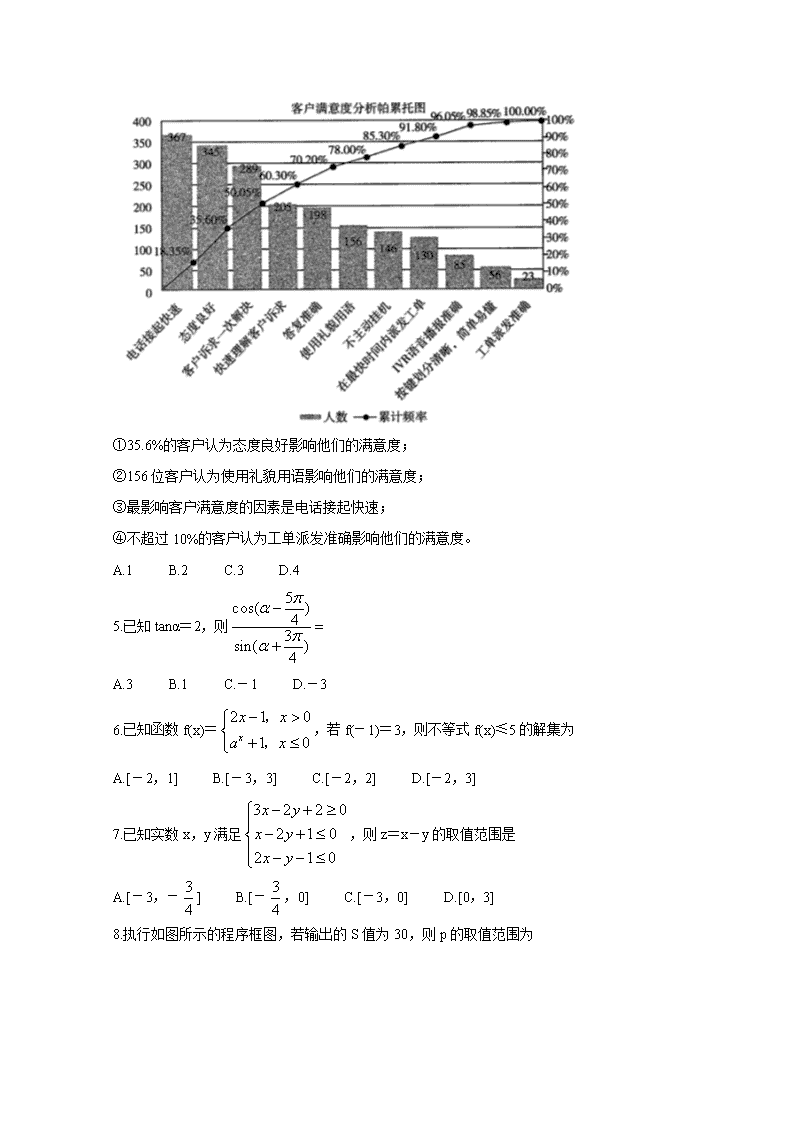
绝密★启用前 天一大联考 ‎2019－2020学年高中毕业班阶段性测试(五)‎ 文科数学 考生注意：‎ ‎1.答题前，考生务必将自己的姓名、考生号填写在试卷和答题卡上，并将考生号条形码粘贴在答题卡上的指定位置。‎ ‎2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ ‎3.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有项是符合题目要求的。‎ ‎1.已知集合A＝{－1，1，2，3，5}，B＝{x∈N|(x－1)(x－5)<0}，则B＝‎ A.{3} B.{2，3} C.{2，3，5} D.{－1，1，5}‎ ‎2.已知复数z＝＋i，则z的共轭复数为 A.1＋3i B.1－3i C.－1＋3i D.－1－3i ‎3.在一堆从实际生活得到的十进制数据中，一个数的首位数字是d(d＝1，2，…，9)的概率为lg(1＋)，这被称为本福特定律。以此判断，一个数的首位数字是1的概率约为 A.10% B.11% C.20% D.30%‎ ‎4.某公司以客户满意为出发点，随机抽选2000名客户，以调查问卷的形式分析影响客户满意度的各项因素。每名客户填写一个因素，下图为客户满意度分析的帕累托图。帕累托图用双直角坐标系表示，左边纵坐标表示频数，右边纵坐标表示频率，分析线表示累计频率，横坐标表示影响满意度的各项因素，按影响程度(即频数)的大小从左到右排列，以下结论正确的个数是 ‎①35.6%的客户认为态度良好影响他们的满意度；‎ ‎②156位客户认为使用礼貌用语影响他们的满意度；‎ ‎③最影响客户满意度的因素是电话接起快速；‎ ‎④不超过10%的客户认为工单派发准确影响他们的满意度。‎ A.1 B.2 C.3 D.4‎ ‎5.已知tanα＝2，则 ‎ A.3 B.1 C.－1 D.－3‎ ‎6.已知函数f(x)＝，若f(－1)＝3，则不等式f(x)≤5的解集为 A.[－2，1] B.[－3，3] C.[－2，2] D.[－2，3]‎ ‎7.已知实数x，y满足，则z＝x－y的取值范围是 A.[－3，－] B.[－，0] C.[－3，0] D.[0，3]‎ ‎8.执行如图所示的程序框图，若输出的S值为30，则p的取值范围为 A.(18，30] B.[18，30] C.(0，30] D.[18，30)‎ ‎9.已知函数f(x)＝sin(＋x)与g(x)＝sin(2x＋φ)(0≤φ<π)的图象有一个横坐标为的交点，将函数g(x)的图象向左平移个单位长度，所得图象的一条对称轴方程为 A.x＝－ B.x＝ C.x＝ D.x＝‎ ‎10.已知函数f(x)，g(x)的定义域为R，f(x＋1)是奇函数，g(x＋1)是偶丽数，若y＝f(x)·g(x)的图象与x轴有5个交点，则y＝f(x)·g(x)的零点之和为 A.－5 B.5 C.－10 D.10‎ ‎11.已知直四棱柱ABCD－A1B1C1D1的侧棱长为8，底面矩形的面积为16，一个小虫从C点出发沿直四棱柱侧面绕行一周后到达线段CC1上一点M，若AM⊥平面A1BD，则小虫爬行的最短路程为 A.8 B.16 C.2 D.4‎ ‎12.已知从圆C：x2＋y2＝r2(r>0)上一点Q(0，r)作两条互相垂直的直线与椭圆τ：相切，同时圆C与直线l：mx＋y－m－1＝0交于A，B两点，则|AB|的最小值为 A.2 B.4 C.4 D.8‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.在等边三角形ABC中，AB＝2，E，F分别为AB，BC的中点，则＝ 。‎ ‎14.双曲线C：(0<θ≤)的离心率的最大值是 。‎ ‎15.已知球O的内接正方体ABCD－A1B1C1D1的棱长为1，点P在线段BD1上，‎ 过点P垂直于BD1的平面截球O所得的截面圆的面积为，则线段PB的长为 。‎ ‎16.已知△ABC的内角A，B，C的对边分别为a，b，c，角B为钝角，设△ABC的面积为S，若4bS＝a(b2＋c2－a2)，则sinA＋sinC的取值范围是 。‎ 三、解答题：共70分。解答应写出文字说明，证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22，23题为选考题，考生根据要求作答。‎ ‎(一)必考题：共60分。‎ ‎17.(12分)‎ 已知数列{an}满足2nan＝2n＋1an＋1－1，数列{bn}是各项均为正数的等比数列，且b4b6＝4b5b7，a1＝b1＝1。‎ ‎(I)求{an}和{bn}的通项公式；‎ ‎(II)设pn＝，求数列{pn}的前2n项和S2n。‎ ‎18.(12分)‎ 如图，已知圆柱内有一个三棱锥A－BCD，AD为圆柱的一条母线，DF，BC为下底面圆O的直径，AD＝BC＝2。‎ ‎(I)在圆柱的上底面圆内是否存在一点E，使得EF//平面ABC？证明你的结论。‎ ‎(II)设点M为棱AC的中点，，求四棱锥B－ADNM体积的最大值。‎ ‎19.(12分)‎ 某科研小组为了研究一种治疗新冠肺炎患者的新药的效果，选50名患者服药一段时间后，记录了这些患者的生理指标x和y的数据，并统计得到如下的2×2列联表(不完整)：‎ 其中在生理指标x>1.7的人中，设A组为生理指标y≤60的人，B组为生理指标y>60的人，他们服用这种药物后的康复时间(单位：天)记录如下：‎ A组：10，11，12，13，14，15，16‎ B组：12，13，15，16，17，14，25‎ ‎(I)填写上表，并判断是否有95%的把握认为患者的两项生理指标x和y有关系；‎ ‎(II)从A，B两组随机各选1人，A组选出的人记为甲，B组选出的人记为乙，求甲的康复时间比乙的康复时间长的概率。‎ 附：，其中n＝a＋b＋c＋d。‎ ‎20.(12分)‎ 已知O为坐标原点，抛物线C：x2＝2py(p>0)的焦点坐标为(0，)，点A，B在该抛物线上且位于y轴的两侧，＝3。‎ ‎(I)证明：直线AB过定点(0，3)；‎ ‎(II)以A，B为切点作C的切线，设两切线的交点为P，点Q为圆(x－1)2＋y2＝1上任意一点，求|PQ|的最小值。‎ ‎21.(12分)‎ 已知函数f(x)＝ex－2x2。‎ ‎(I)设g(x)＝，判断g(x)在(0，＋∞)上零点的个数；‎ ‎(II)证明：f(x－1)>。‎ ‎(二)选考题：共10分请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分。‎ ‎22.[选修4－4：坐标系与参数方程](10分)‎ 在直角坐标系xOy中，曲线C1的参数方程为(t为参数)。以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρsinθ＝4，M为曲线C2上的动点，点P在线段OM上，且满足|OM|·|OP|＝16。‎ ‎(I)求点P的轨迹C3的直角坐标方程；‎ ‎(II)设C1与C3的交点为A，B，求△AOB的面积。‎ ‎23.[选修4－5：不等式选讲](10分)‎ 若对于实数x，y有|1－2x|≤4，|3y＋1|≤3。‎ ‎(I)求的最大值M；‎ ‎(II)在(I)的条件下，若正实数a，b满足，证明：(a＋1)(b＋2)≥。‎