【数学】2018届一轮复习人教A版利用二分法求方程的近似解问题学案

【数学】2018届一轮复习人教A版利用二分法求方程的近似解问题学案

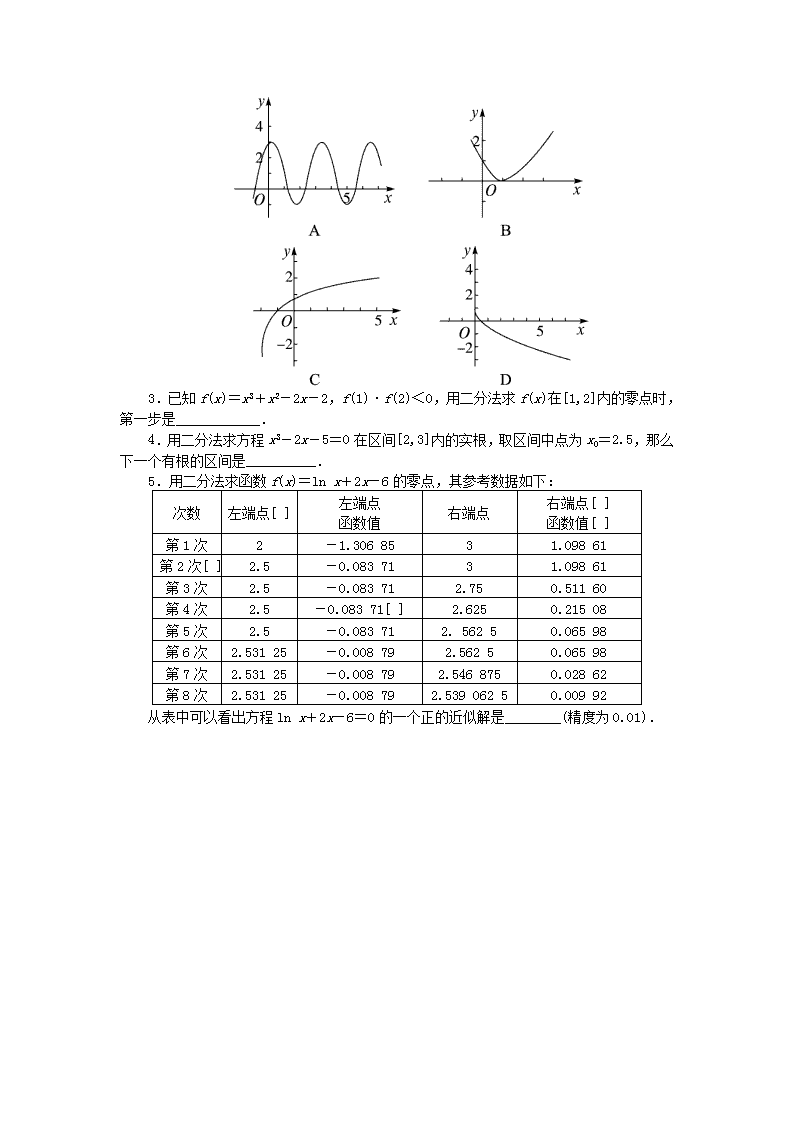
‎4.1.2　‎利用二分法求方程的近似解 问题导学 一、二分法定义的理解 活动与探究1‎ ‎(1)下列图像与x轴均有交点，其中不能用二分法求函数零点的是(　　)．‎ ‎(2)用二分法求方程f (x)＝0的近似解，f(1)＝－2，f(1.5)＝0.625，f(1.25)＝－0.984，f(1.375)＝－0.260，下一个求f(m)，则m＝________.‎ 迁移与应用 ‎(1)下面关于二分法的叙述，正确的是(　　)．‎ A．用二分法可以求所有函数零点的近似值 B．用二分法求方程的近似解时，可以精确到小数点后的任一位 C．二分法无规律可循 D．只有在求函数零点时才用二分法 ‎(2)用二分法求函数f(x)＝x3＋5的零点可以取的初始区间为(　　)．‎ A．[－2,1] B．[－1,0]‎ C．[0,1] D．[1,2]‎ ‎“二分法”与判定函数零点的定义密切相关，只有满足函数图像在零点附近连续且在该零点两侧的函数值异号时才能应用“二分法”求函数零点． ‎ 二、用二分法求方程的近似解 活动与探究2‎ 求方程lg x－2－x＋1＝0的近似解(精度0.1)．‎ 迁移与应用 用二分法求函数f(x)＝x3－x－1在区间[1,1.5]内的近似零点．(精度0.1)‎ 利用二分法求方程的近似解时应注意的问题 ‎(1)注意题目中要求的精度，它决定着二分法到何时结束；‎ ‎(2)选择方程的解可能存在的合适的初始区间，它决定着二分法计算步骤的繁简；‎ ‎(3)题目要求的精度不同，得到的方程的近似解不同．‎ 当堂检测 ‎1．下列函数中不能用二分法求零点的是(　　)．‎ A．f(x)＝3x－1　　　B．f(x)＝x3‎ C．f(x)＝|x| D．f(x)＝ln x ‎2．下列函数图像与x轴均有交点，其中不能用二分法求函数零点的近似值的是(　　)．‎ ‎3．已知f(x)＝x3＋x2－2x－2，f(1)·f(2)＜0，用二分法求f(x)在[1,2]内的零点时，第一步是____________．‎ ‎4．用二分法求方程x3－2x－5＝0在区间[2,3]内的实根，取区间中点为x0＝2.5，那么下一个有根的区间是__________．‎ ‎5．用二分法求函数f(x)＝ln x＋2x－6的零点，其参考数据如下：‎ 次数 左端点[ ] ‎ 左端点 函数值 右端点 右端点[ ]‎ 函数值[ ]‎ 第1次 ‎2‎ ‎－1.306 85‎ ‎3 ‎ ‎1.098 61‎ 第2次[ ]‎ ‎2.5‎ ‎－0.083 71‎ ‎3‎ ‎1.098 61‎ 第3次 ‎2.5‎ ‎－0.083 71‎ ‎2.75‎ ‎0.511 60‎ 第4次 ‎2.5‎ ‎－0.083 71[ ]‎ ‎2.625‎ ‎0.215 08‎ 第5次 ‎2.5‎ ‎－0.083 71‎ ‎2. 562 5 ‎ ‎0.065 98‎ 第6次 ‎2.531 25‎ ‎－0.008 79‎ ‎2.562 5‎ ‎0.065 98‎ 第7次 ‎2.531 25‎ ‎－0.008 79‎ ‎2.546 875‎ ‎0.028 62‎ 第8次 ‎2.531 25‎ ‎－0.008 79‎ ‎2.539 062 5 ‎ ‎0.009 92‎ 从表中可以看出方程ln x＋2x－6＝0的一个正的近似解是________(精度为0.01)．‎