2020届二轮复习函数的奇偶性课件（23张）（全国通用）

2020届二轮复习函数的奇偶性课件（23张）（全国通用）

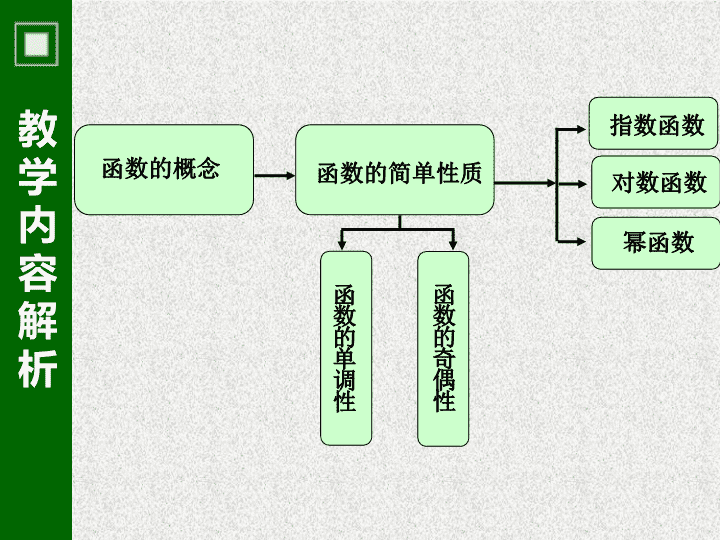
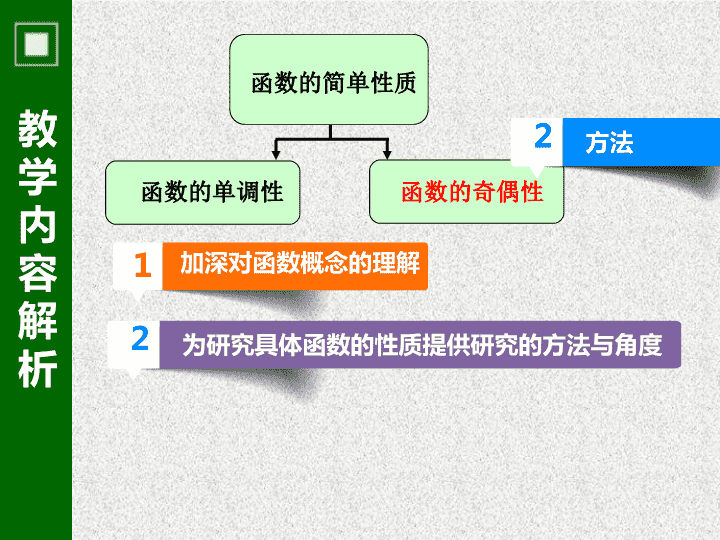
01 教学内容解析 说课 02 教学目标设置 03 学生学情分析 04 教学策略分析 05 教学过程设计 教学内容解析 函数的 概念 函数的简单性质 函数的奇偶性 函数的单调性 幂函数 指数 函数 对数 函数 教学内容解析 函数的简单性质 函数的 单调性 函数 的奇偶性 知识 1 加深对函数概念的理解 1 方法 2 为研究具体函数的性质提供研究的方法与角度 2 教学内容解析 教学内容： 函数的奇偶性的定义及其判定 教学重点： 建构函数的奇偶性的概念并会判 断一个函数是否具有奇偶性 教学目标设置 教学目标设置 2 1 教学目标 3 2 1 3 教学目标 教学目标设置 会用数量关系判断函数图象关于 y 轴对称或关于原点对 称，在此基础上建构函数的奇偶性的定义 ； 3 2 1 教学目标 教学目标设置 能正确判断具体函数是 否具有奇偶性； 1 3 2 教学目标 教学目标设置 运用数形结合的思想，经历从特殊到一般，从具体到抽象的研究过程，进一步体验研究函数性质的一般方法。 学生学情分析 知识 方法 能力 学生学情分析 教学难点： 对关系式 f ( - x ) = f ( x ) （ 或 f ( - x ) =- f ( x ) ） 的理解 学生学情分析 观察分析 自主探索 合作交流 类比探究 教学策略分析 建构函数的奇偶性的概念 引导应用 引导探究 创设情境 回顾反思 理解领悟 自主探索 直观感受 深化认识 教学过程设计 01 03 02 创设情境，引出新课 探究发现，建构概念 自我尝试，应用概念 04 回顾总结，深化理解 教学过程设计 创设情境，引出新课 教学过程设计 创设情境，引出新课 你能说出它们分别是什么对称图形吗？ 数学中有哪些对称的现象？ 以上函数中，最简单最基本的对称是什么？ 哪些函数的图象具有对称性？ 教学过程设计 探究发现，建构概念 问题串 如何判定函数 图象 关于 轴对称 ？ 如何判定函数 图象 关于 轴对称 ？ 你能给出偶函数的定义吗？ 教学过程设计 探究发现，建构概念 问题串 如何判定函数 图象关于原点对称 ？ 你能给出奇函数的定义吗？ 教学过程设计 自我尝试，应用概念 拓展 开放 例题 教学过程设计 1. 说一说奇函数与偶函数的异同 . 回顾总结，深化概念 2. 若偶函数 y = f ( x ) 在 上 为增函数，你能判断它在 上的单调性吗？