2019届二轮复习　平面向量与数学文化课件（32张）（全国通用）

2019届二轮复习　平面向量与数学文化课件（32张）（全国通用）

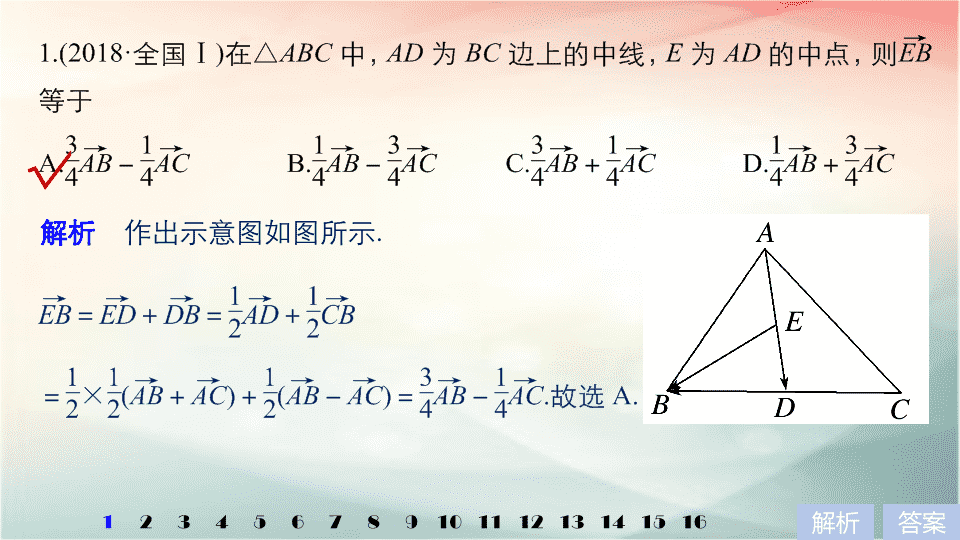
第 4 讲　平面向量与数学文化 板块二　练透基础送分小考点 [ 考情考向分析 ] 1. 考查平面向量的基本定理及基本运算，多以熟知的平面图形为背景进行考查，多为选择题、填空题，难度为中低档 . 2 . 考查平面向量的数量积，以选择题、填空题为主，难度为低档；向量作为工具，还常与三角函数、解三角形、不等式、解析几何结合，以解答题形式出现 . 3 . 考查以数学文化为背景的新颖命题，解决的关键是抽象出相应的数学问题，问题的背景主要涉及：程序框图、数列、概率统计、平面图形及空间几何体 . 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 √ 解析　 作出示意图如图所示 . 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 2.(2018· 全国 Ⅱ ) 已知向量 a ， b 满足 | a | ＝ 1 ， a·b ＝－ 1 ，则 a ·(2 a － b ) 等于 A.4 B.3 C.2 D.0 √ 解析　 a ·(2 a － b ) ＝ 2 a 2 － a · b ＝ 2| a | 2 － a · b . ∵ | a | ＝ 1 ， a · b ＝－ 1 ， ∴ 原式＝ 2 × 1 2 ＋ 1 ＝ 3. 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 3.(2018· 百校联盟 TOP20 联考 ) 已知 a ＝ ( x, 1) ， b ＝ ( － 2,4) ，若 ( a ＋ b ) ⊥ b ，则 x 等于 A.8 B.10 C.11 D.12 √ 解析 解析　 ∵ a ＝ ( x, 1) ， b ＝ ( － 2,4) ， ∴ a ＋ b ＝ ( x － 2,5) ， 又 ( a ＋ b ) ⊥ b ， ∴ ( x － 2) × ( － 2) ＋ 20 ＝ 0 ， ∴ x ＝ 12. 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 4.(2018· 张家界模拟 ) 数的概念起源于大约 300 万年前的原始社会，如图 1 所示，当时的人类用在绳子上打结的方法来记数，并以绳结的大小来表示野兽的大小，即 “ 结绳计数 ”. 图 2 所示的是某个部落一段时间内所擒获猎物的数量，在从右向左依次排列的不同绳子上打结，右边绳子上的结每满 7 个即在左边的绳子上打一个结，请根据图 2 计算该部落在该段时间内所擒获的猎物总数为 A.336 B.510 C.1 326 D.3 603 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 由题意知，图 2 中的 “ 结绳计数 ” 法是七进制计数法，所以图 2 计算该部落在该段时间内所擒获的猎物总数为 S ＝ 1 × 7 3 ＋ 3 × 7 2 ＋ 2 × 7 1 ＋ 6 × 7 0 ＝ 510. 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 5.(2018· 北京师范大学附中模拟 ) 习总书记在十九大报告中指出：坚定文化自信，推动社会主义文化繁荣兴盛 . 如图， “ 大衍数列 ” ： 0,2,4,8,12 来源于《乾坤谱》中对《易传》 “ 大衍之数五十 ” 的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和 . 如图是 求 大 衍数列前 n 项和的程序框图 . 执行 该 程序框图 ， 输入 m ＝ 8 ， 则输出的 S 等于 A.44 B.68 C.100 D.140 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 第 1 次运行， n ＝ 1 ， a ＝ ＝ 0 ， S ＝ 0 ＋ 0 ＝ 0 ，不符合 n ≥ m ，继续运行； 第 2 次运行， n ＝ 2 ， a ＝ ＝ 2 ， S ＝ 0 ＋ 2 ＝ 2 ，不符合 n ≥ m ，继续运行； 第 3 次运行， n ＝ 3 ， a ＝ ＝ 4 ， S ＝ 4 ＋ 2 ＝ 6 ，不符合 n ≥ m ，继续运行； 第 4 次运行， n ＝ 4 ， a ＝ ＝ 8 ， S ＝ 8 ＋ 6 ＝ 14 ，不符合 n ≥ m ，继续运行； 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 第 5 次运行， n ＝ 5 ， a ＝ ＝ 12 ， S ＝ 14 ＋ 12 ＝ 26 ，不符合 n ≥ m ，继续运行； 第 6 次运行， n ＝ 6 ， a ＝ ＝ 18 ， S ＝ 26 ＋ 18 ＝ 44 ，不符合 n ≥ m ，继续运行； 第 7 次运行， n ＝ 7 ， a ＝ ＝ 24 ， S ＝ 24 ＋ 44 ＝ 68 ，不符合 n ≥ m ，继续运行； 第 8 次运行， n ＝ 8 ， a ＝ ＝ 32 ， S ＝ 68 ＋ 32 ＝ 100 ，符合 n ≥ m ，退出运行，输出 S ＝ 100. 6.(2018· 百校联盟 TOP20 联考 ) 中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他活动的民间艺术，在中国，剪纸具有 广泛的群众基础，交融于各族人民的社会生活，是各种民俗活动的重要组成部分 . 在如图所示的古代正八边形窗花矢量图片中 ， ， 则向正八边形窗花矢量图片中任投一点，落在正方形 DEFG 中的概率为 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 7.(2018· 湖南 G10 教育联盟联考 ) 天干地支纪年法源于中国，中国自古便有十天干与十二地支 . 十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸；十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥 . 天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由 “ 甲 ” 起，地支由 “ 子 ” 起，例如，第一年为 “ 甲子 ” ，第二年为 “ 乙丑 ” ，第三年为 “ 丙寅 ” ， … ，以此类推，排列到 “ 癸酉 ” 后，天干回到 “ 甲 ” 重新开始，即 “ 甲戌 ” ， “ 乙亥 ” ，然后地支回到 “ 子 ” 重新开始，即 “ 丙子 ” ，以此类推 . 已知 1949 年为 “ 己丑 ” 年，那么到中华人民共和国成立 80 年时为 A. 丙酉年 B. 戊申年 C . 己申年 D . 己酉年 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 天干是以 10 为公差的等差数列，地支是以 12 为公差的等差数列， 从 1949 年到 2029 年经过 80 年，且 1949 年为 “ 己丑 ” 年，以 1949 年的天干和地支分别为首项，则 80÷10 ＝ 8 ，则 2029 的天干为己， 80÷12 ＝ 6 余 8 ，则 2029 的地支为酉，故选 D. 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 √ 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 √ 解析　 如图所示， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 10.(2018· 西宁模拟 ) 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理： “ 幂势既同，则积不容异 ”. 其中 “ 幂 ” 是截面积， “ 势 ” 是几何体的高，意思是两等高立方体，若在每一等高处的截面积都相等，则两立方体的体积相等，已知某不规则几何体与如图所示的三视图所表示的几何体满足 “ 幂势同 ” ，则该不规则几何体的体积 为 √ 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 　 由祖 暅 原理可知 ，该不规则几何体的体积与已知三视图几何体体积相等，由三视图知几何体是一个正方体去掉一个半圆柱，如图 ： 11.(2018· 衡水金卷调研卷 ) 《九章算术》卷第五《商功》中有记载： “ 刍甍者，下有袤有广，而上有袤无广 . 刍，草也 . 甍，屋盖也 . ” 翻译为 “ 底面有长有宽为矩形，顶部只有长没有宽为一条棱 . 刍 甍 字面 意 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 思 为茅草屋顶 . ” 现有一个刍甍，如图，四边形 ABCD 为正方形，四边形 ABFE ， CDEF 为两个全等的等腰梯形， AB ＝ 4 ， EF ∥ AB ，且 EF ＝ AB ，若这个刍甍的体积 为 ， 则 CF 的长为 A.1 B.2 C.3 D.4 √ 解析 　 取 CD ， AB 的中点分别为 M ， N ，连接 FM ， FN ， MN ， 则多面体分割为棱柱与棱锥部分，设 E 到平面 ABCD 的距离为 h ， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 依题意可知，点 E ， F 在平面 ABCD 内的射影恰好是 DN 与 CN 的中点， 答案 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 √ 解析　 如图，以 D 为坐标原点， DA ， DC 所在直线分别为 x 轴， y 轴，建立平面直角坐标系 . 连接 AC ， 由 题意知 ∠ CAD ＝ ∠ CAB ＝ 60° ， ∠ ACD ＝ ∠ ACB ＝ 30° ， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 13.(2018· 全国 Ⅲ ) 已知向量 a ＝ (1,2) ， b ＝ (2 ，－ 2) ， c ＝ (1 ， λ ). 若 c ∥ (2 a ＋ b ) ，则 λ ＝ ________. 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 由题意得 2 a ＋ b ＝ (4,2) ， 因为 c ∥ (2 a ＋ b ) ，所以 4 λ ＝ 2 ， 答案 14.(2018· 辽宁省辽南协作校模拟 ) 设向量 a ＝ (1 ， ) ， b ＝ ( m ， ) ，且 a ， b 的夹角为锐角，则实数 m 的取值范围是 ___________________. 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 ( － 3,1) ∪ (1 ，＋ ∞ ) 解析 解析 　 因为 a ， b 的夹角为锐角， 所以 a · b ＝ m ＋ 3>0 ，解得 m > － 3 ， 又当 m ＝ 1 时，〈 a ， b 〉＝ 0 不符合题意， 所以 m > － 3 且 m ≠ 1. 15.(2018· 湖北七市 ( 州 ) 教研协作体联考 ) 《数书九章》三斜求积术： “ 以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂，减上，余四约一，为实，一为从隅，开平方得积 ”. 秦九韶把三角形的三条边分别称为小斜、中斜和大斜， “ 术 ” 即方法 . 以 S ， a ， b ， c 分别表示三角形的面积，大斜，中斜，小斜； h a ， h b ， h c 分别为对应的大斜， 中 斜 ，小斜上的高； 则 若 在 △ ABC 中 h a ＝ ， h b ＝ 2 ， h c ＝ 3 ，根据上述公式，可以推出该 三角形 外接圆 的半径为 ________. 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 16.(2018· 天津市十二校模拟 ) 已知直角梯形 ABCD 中， AD ∥ BC ， ∠ BAD ＝ 90° ， ∠ ADC ＝ 45° ， AD ＝ 2 ， BC ＝ 1 ， P 是腰 CD 上的动点 ， 则 的 最小值为 ________. 解析 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 答案 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 解析　 以 D 为坐标原点， DA 为 x 轴，过 D 与 DA 垂直的直线为 y 轴，建立平面直角坐标系， 由 AD ∥ BC ， ∠ BAD ＝ 90° ， ∠ ADC ＝ 45° ， AD ＝ 2 ， BC ＝ 1 ， 可得 D (0,0) ， A (2,0) ， B (2,1) ， C (1,1) ， ∵ P 在 CD 上， ∴ 可设 P ( t ， t )(0 ≤ t ≤ 1) ， 1 2 3 4 5 6 7 8 9 10 11 12 14 13 16 15 本课结束