【数学】2020届一轮复习人教A版算法与程序框图学案

【数学】2020届一轮复习人教A版算法与程序框图学案

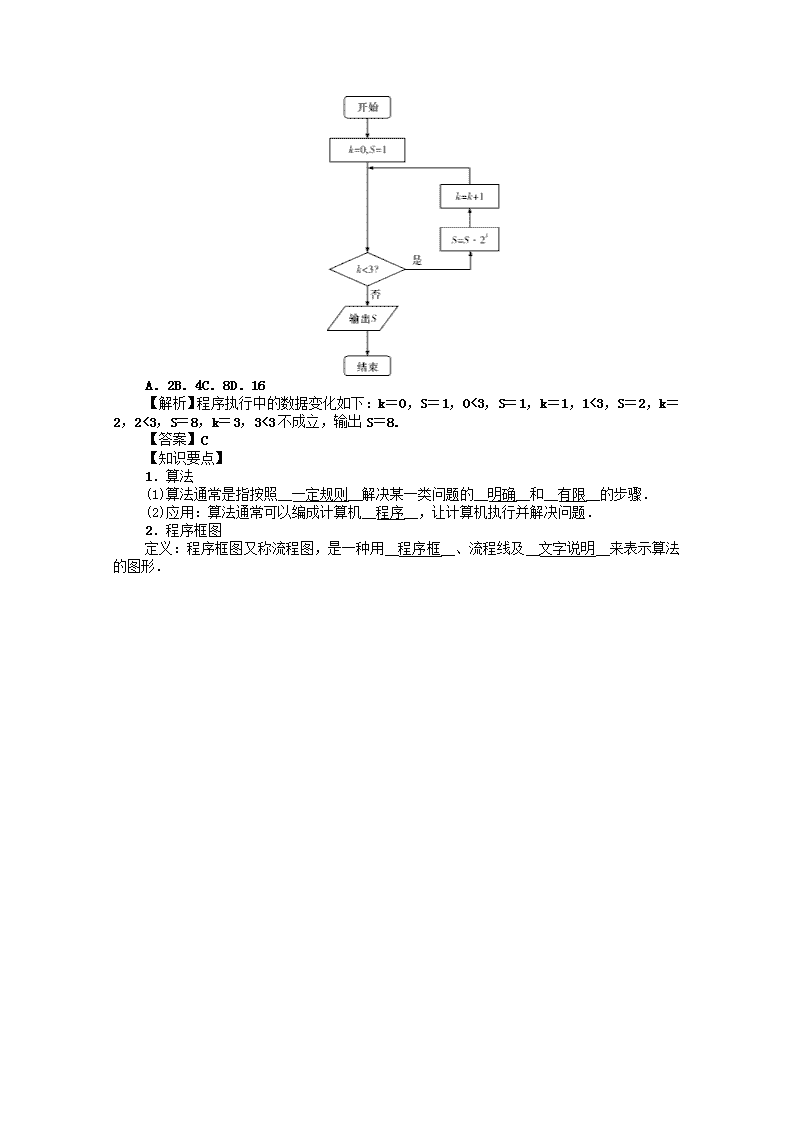
第4讲　算法与程序框图 夯实基础　【p8】‎ ‎【学习目标】‎ ‎1．了解算法的含义、了解算法的思想；理解程序框图的三种基本逻辑结构：顺序、条件分支、循环．‎ ‎2．理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．‎ ‎3．初步了解几个典型算法案例．‎ ‎4．了解程序框图，了解工序流程图(即统筹图)，能绘制简单实际问题的流程图，了解流程图在解决实际问题中的作用；了解结构图，会用结构图梳理已学过的知识、整理收集到的资料信息．‎ ‎【基础检测】‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1．程序框图中表示计算的是(　　)‎ ‎【解析】A中执行框可表示计算；B中为输入输出框；C中为判断框；D中为起止框．‎ ‎【答案】A ‎2．下列给出的赋值语句中正确的是(　　)‎ A．x＝1B．x＝y＝5‎ C．x＋1＝yD．x＋y＝0‎ ‎【解析】根据赋值号左边只能是变量，右边可以是任意表达式，故选A.‎ ‎【答案】A ‎3．如图所示，当输入a，b的值分别为2，3时，最后输出的M的值是(　　)‎ INPUTa，b IFa>bTHEN　　‎ ‎　M＝a ELSE ‎　M＝b ENDIF PRINTM A．1B．2C．3D．4‎ ‎【解析】算法是求a，b中的较大者，故最后输出的是3，故选C.‎ ‎【答案】C ‎4．执行如图所示的程序框图，输出的S值为(　　)‎ A．2B．4C．8D．16‎ ‎【解析】程序执行中的数据变化如下：k＝0，S＝1，0<3，S＝1，k＝1，1<3，S＝2，k＝2，2<3，S＝8，k＝3，3<3不成立，输出S＝8.‎ ‎【答案】C ‎【知识要点】‎ ‎1．算法 ‎(1)算法通常是指按照__一定规则__解决某一类问题的__明确__和__有限__的步骤．‎ ‎(2)应用：算法通常可以编成计算机__程序__，让计算机执行并解决问题．‎ ‎2．程序框图 定义：程序框图又称流程图，是一种用__程序框__、流程线及__文字说明__来表示算法的图形．‎ ‎3.三种基本逻辑结构 ‎　　名称 内容　　‎ 顺序结构 条件结构 循环结构 定义 由若干个__依次执行__的步骤组成，这是任何一个算法都离不开的__基本结构__‎ 算法的流程根据__条件是否成立__有不同的流向，条件结构就是处理这种过程的结构 从某处开始，按照一定的条件__反复执行__某些步骤的情况，反复执行的步骤称为__循环体__‎ 程序框图 ‎　　4.进位制 ‎①将十进制数化为二进制数的算法称为__除2取余法__；将十进制数化为k进制数的算法称为除k取余法．‎ ‎②将k进制数化为十进制数的算法步骤为：‎ 第一步：从左到右依次取k进制数anan－1…a1a0(k)各位上的数字乘以k的幂，k的幂从n开始取值，每次递减1，递减到0，即an·kn，an－1·kn－1，…，a1·k，a0·k0；‎ 第二步：把所有积加起来，就得到十进制数．‎ 典例剖析　【p9】‎ 考点1　顺序结构和条件结构 ‎　　　　　　　　　　　　　　　　　　　‎ (1)执行如图所示的程序框图，输出的S值为(　　)‎ A．2B．2.5C．3.5D．4‎ ‎【解析】因为a＝2，b＝4，‎ 所以S＝＋＝＋＝2.5.‎ 故选B.‎ ‎【答案】B ‎(2)执行下面的程序框图，当输入的x的值为4时，输出的y的值为2，则空白判断框中的条件可能为(　　)‎ A．x>3?B．x>4?‎ C．x≤4?D．x≤5?‎ ‎【解析】输入x的值为4时，由x＋2＝6，log24＝2可知x＝4不满足判断框中的条件，只能是x>4？，故选B.‎ ‎【答案】B ‎(3)在如图所示的框图中，若输出S＝360，那么判断框中应填入的关于k的判断条件是(　　)‎ A．k>2?B．k<2?C．k>3?D．k<3?‎ ‎【解析】当S＝1时不满足退出循环的条件，执行循环体后，S＝6，k＝5；‎ 当S＝6时不满足退出循环的条件，执行循环体后，S＝30，k＝4；‎ 当S＝30时不满足退出循环的条件，执行循环体后，S＝120，k＝3；‎ 当S＝120时不满足退出循环的条件，执行循环体后，S＝360，k＝2；‎ 当S＝360时满足退出循环的条件，‎ 故判断框中应填入的关于k的判断条件是k<3，故选D.‎ ‎【答案】D ‎【小结】(1)注意区分处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．‎ ‎(2)给出初始条件和输出结果，分析判断框中的条件，有顺推和逆推两种方法．‎ 考点2　循环结构 (1)执行如图所示的程序框图，输出的S值为(　　)‎ A．2B.C.D. ‎【解析】k＝0时，0<3成立，第一次进入循环：k＝1，S＝＝2；1<3成立，第二次进入循环：k＝2，S＝＝；2<3成立，第三次进入循环：k＝3，S＝＝，3<3不成立，输出S＝，故选C.‎ ‎【答案】C ‎(2)阅读下面的程序框图，运行相应的程序，若输入N的值为19，则输出N的值为(　　)‎ A．0B．1C．2D．3‎ ‎【解析】初始N＝19，进入循环后N的值依次为N＝18，N＝6，N＝2，结束循环，输出N＝2，故选C.‎ ‎【答案】C ‎(3)已知数列中，a1＝1，an＋1＝an＋n，若利用如图所示的程序框图计算该数列的第10项，则判断框内的条件是(　　)‎ A．n<6?B．n<7?C．n≤8?D．n≤9?‎ ‎【解析】第一次循环：1≤m成立，S＝a2，n＝2，依次类推，第九次循环：9≤m成立，S＝a10，n＝10，第十次循环：10≤m不成立，输出第10项，因此9≤m<10，选D.‎ ‎【答案】D ‎【小结】(1)循环结构中必有选择结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．‎ ‎(2)直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．‎ 考点3　基本算法结构 (1)执行下边的程序框图，若输入的x的值为1，则输出的y的值是________．‎ ‎【解析】当x＝1时，1<2，则x＝1＋1＝2；当x＝2时，不满足x<2，则y＝3×22＋1＝13.‎ ‎【答案】13‎ ‎(2)下图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为8，10，0，则输出a和i的值分别为(　　)‎ A．2，4B．2，5C．0，4D．0，5‎ ‎【解析】模拟执行程序框图，可得a＝8，b＝10，i＝0，‎ i＝1，不满足a>b，‎ 不满足a＝b，b＝10－8＝2，i＝2；‎ 满足a>b，a＝8－2＝6，i＝3；‎ 满足a>b，a＝6－2＝4，i＝4；‎ 满足a>b，a＝4－2＝2，i＝5；‎ 不满足a>b，满足a＝b，输出a的值为2，i的值为5，故选B.‎ ‎【答案】B ‎(3)随机抽取某中学甲、乙两个班各10名同学，测量他们的身高获得身高数据的茎叶图如图．在样本的20人中，记身高在[150，160)，[160，170)，[170，180)，[180，190)的人数依次为A1，A2，A3，A4.如图是统计样本中身高在一定范围内的人数的算法框图．若图中输出的S＝18，则判断框内应填________．‎ ‎【解析】由于i从2开始，也就是统计身高大于或等于160的所有人数，于是就要计算A2＋A3＋A4，因此，判断框内应填i＜5？或i≤4？.‎ ‎【答案】i＜5？(或i≤4？)‎ ‎【小结】解决程序框图基本问题的3个常用变量及1个关键点：‎ ‎(1)3个常用变量 ‎①计数变量：用来记录某个事件发生的次数，如i＝i＋1.‎ ‎②累加变量：用来计算数据之和，如S＝S＋i.‎ ‎③累乘变量：用来计算数据之积，如p＝p×i.‎ ‎(2)1个关键点 处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．‎ 考点4　算法案例 (1)用辗转相除法求得数98与63的最大公约数是________．‎ ‎【解析】98÷63＝1…35，63÷35＝1…28，35÷28＝1…7，28÷7＝4…0，所以最大公约数是7.‎ ‎【答案】7‎ ‎(2)把18化成二进制数是(　　)‎ A．1001(2)B．1010(2)‎ C．10001(2)D．10010(2)‎ ‎【解析】利用除k取余法把18化成二进制数．‎ 故18＝10010(2)，故答案为D.‎ ‎【答案】D ‎(3)用秦九韶算法计算多项式f(x)＝3x6＋5x5＋6x4＋79x3－8x2＋35x＋12，x＝－4时，求v3的值．‎ ‎【解析】∵f(x)＝3x6＋5x5＋6x4＋79x3－8x2＋35x＋12‎ ‎＝(((((3x＋5)x＋6)x＋79)x－8)x＋35)x＋12，∴v0＝3，‎ v1＝v0x＋5＝3×(－4)＋5＝－7, ‎ v2＝v1x＋6＝－7×(－4)＋6＝34, ‎ v3＝v2x＋79＝34×(－4)＋79＝－57, ‎ ‎∴v3的值为－57.‎ ‎【小结】秦九韶算法是多项式求值的优秀算法，其特点是：‎ ‎①化高次多项式求值为一次多项式求值；‎ ‎②减少了运算次数，提高了效率；‎ ‎③步骤重复执行，容易用计算机实现．‎ 利用秦九韶算法计算多项式的值关键是能正确地将所给多项式改写，然后由内向外逐次计算，由于后项计算用到前项的结果，故应认真、细心，确保中间结果的准确性，若在多项式中有几项不存在，可将这些项的系数看成0，即把这些项看作0×xn.‎ ‎【能力提升】‎ 执行下面的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为(　　)‎ A．5B．4C．3D．2‎ ‎【解析】当输入的正整数N是所给选项中最小的正整数2时，t＝1，M＝100，S＝0，则第一次循环，S＝0＋100＝100，M＝－＝－10，t＝2；第二次循环，S＝100－10＝90，M＝－＝1，t＝3，此时t≤2不成立，输出S＝90<91，故选D.‎ ‎【答案】D 方法总结　【p11】‎ ‎1．了解算法思想，理解算法含义的关键在于体现程序或步骤的明确性和有效性．‎ ‎2．深刻理解三种程序框图的属性与特征，需通过实际例子体会算法流程的全过程，认清所解决问题的实质．如解决分段函数的求值问题时，一般采用条件结构设计算法；如累加求和，累乘求积等问题．‎ ‎3．阅读程序框图应注意：‎ ‎(1)弄清相应操作框的内容；‎ ‎(2)带箭头的流程线及判断框的条件；‎ ‎(3)框内外必要的文字说明和算法功能．‎ ‎4．编写程序的关键是搞清问题的算法，特别是算法结构，然后确定采用哪一种算法语句．‎ ‎5．对于实际问题，应先建立函数模型，然后设计算法．‎ ‎6．(1)辗转相除法与更相减损术是求两个正整数的最大公约数的两种方法，关键是掌握这两种算法的操作步骤，计算时应认真、细心，确保中间结果的准确性，因为下一次计算要用到上一次计算的结果．‎ ‎(2)利用“除k取余法”将十进制数化为k进制数时，要把各步所得余数从下到上排，‎ 切莫把顺序弄错．‎ ‎(3)利用秦九韶算法计算多项式的值的关键是正确地将多项式改写，然后由内向外逐次计算．由于下一次计算要用到上一次计算的结果，同样应认真、细致地计算每一步，确保每一步结果的准确性．‎ 走进高考　　【p11】‎ ‎1．(2018·江苏)一个算法的伪代码如图所示，执行此算法，最后输出的S的值为____________．‎ I←1‎ S←1‎ WHILE　I<6　　‎ ‎　I←I＋2‎ ‎　S←2S ‎　END　WHILE PRINTS ‎【解析】该伪代码运行3次，第1次，I＝3，S＝2；第2次，I＝5，S＝4；第3次，I＝7，S＝8，结束运行．故输出的S的值为8.‎ ‎【答案】8‎ ‎2．(2018·全国卷Ⅱ)为计算S＝1－＋－＋…＋－，设计了如下程序框图，则在空白框中应填入(　　)‎ A．i＝i＋1B．i＝i＋2‎ C．i＝i＋3D．i＝i＋4‎ ‎【解析】由S＝1－＋－＋…＋－得程序框图先分别对奇数项累加，偶数项累加，最后再相减．因此在空白框中应填入i＝i＋2，选B.‎ ‎【答案】B