2019届二轮复习解题技巧圆锥曲线中必考的双曲线问题学案(全国通用)
考纲要求:
1.了解双曲线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线). 2.了解双曲线的实际背景及双曲线的简单应用. 3.理解数形结合的思想.
基础知识回顾:
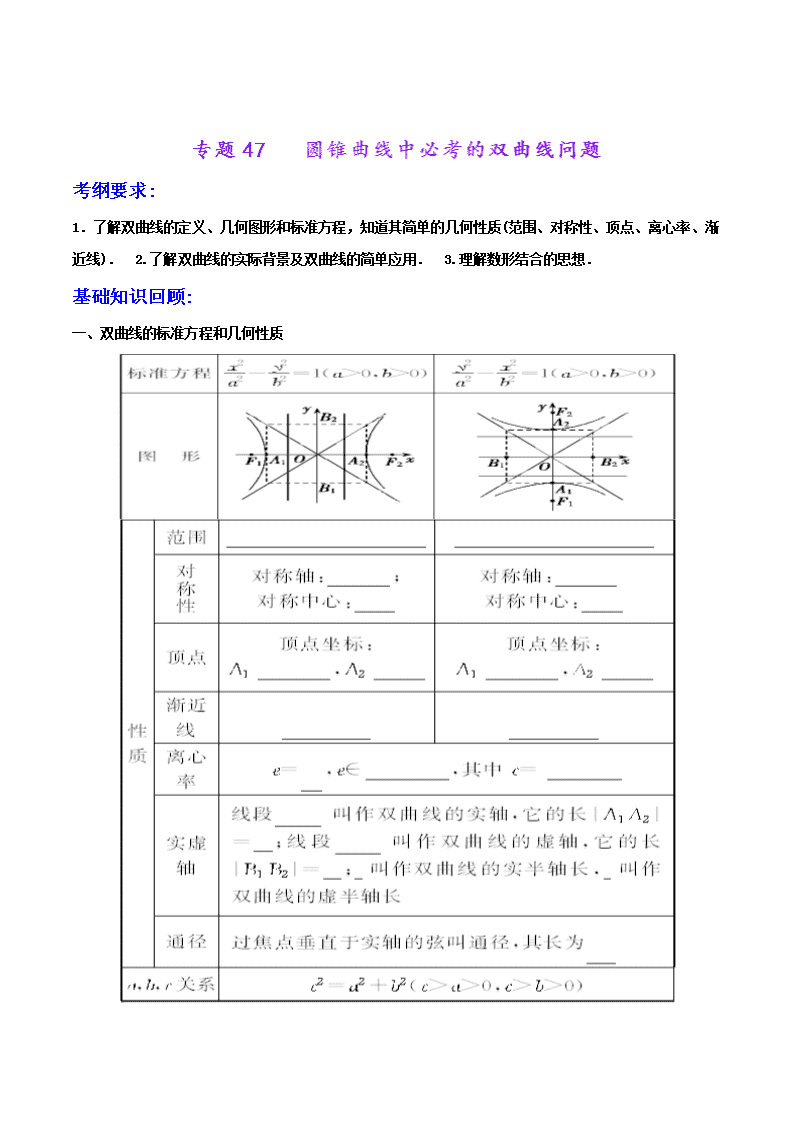
一、双曲线的标准方程和几何性质
或 或 坐标轴 坐标轴 原点 原点
二、 双曲线的定义:
平面内到两定点F1,F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.
集合P={M |MF1|-|MF2 =2a,|F1F2|=2c,其中a、c为常数且a>0,c>0}.
(1)当a
c时,P点不存在.
应用举例:
类型一、利用定义解决焦点三角形问题
【例1】椭圆与双曲线有相同的焦点,点是椭圆与双曲线的一个交点,则的面积是( )
A. 4 B. 2 C. 1 D.
【答案】C
【解析】
【分析】
根据椭圆与双曲线定义解得再根据解三角形得面积.
【点睛】
本题考查椭圆与双曲线定义以及解焦点三角形,考查基本分析求解能力.属中档题.
【例2】【名校联盟2018年高考第二次适应与模拟】已知O是坐标原点,双曲线与椭圆的一个交点为P,点,则的面积为( )
A. B. C. D.
【答案】D
【解析】
【分析】
由椭圆与双曲线的定义可得 , = ,由标准方程可得=,结合余弦定理、勾股定理以及椭圆的对称性可得结果.
由椭圆与双曲线的标准方程方程=,
所以与重合,由余弦定理得到
,
故 ,
则的面积为, 故答案为D.
【点睛】
本题主要考查利用椭圆与双曲线的定义、简单性质求标准方程,属于中档题.求解与椭圆、双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点等基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.
【例3】【四川省南充高级中学2018届高三考前模拟考试】为双曲线右支上一点,分别为双曲线的左、右焦点,且,直线交轴于点,则的内切圆半径为( )
A. B. C. D.
【答案】A
【解析】分析:根据题意,由双曲线的标准方程可得a的值,设的内切圆半径为r,由直角三角形的性质分析可得,由双曲线的几何性质分析,由图形的对称性知2r-4=0,即可得答案.
详解:根据题意,双曲线,其中,
点睛:本题考查了双曲线的几何性质、双曲线的定义,注意直角三角形的内切圆公式.
类型二、求渐近线方程
1、利用离心率求渐近线方程
【例4】【山东省青岛市2019届高三9月期初调研检测】已知双曲线的离心率e=2,则双曲线C的渐近线方程为
A. B.
C. D.
【答案】D
【解析】
【分析】
根据离心率e=,由a,b,c的关系得到,进而得到渐近线方程.
【点睛】
这个题目考查的是双曲线的几何意义,已知离心率得到a,b,c的关系式,进而得到渐近线方程.
2、利用几何性质求渐近线方程
【例5】【东北师范大学附属中学2018届高三第五次模拟考试】已知双曲线方程为,它的一条渐近线与圆相切,则双曲线的离心率为( )
A. B. C. D.
【答案】A
【解析】
方法一:双曲线的渐近线方程为,则,圆的方程,圆心为,所以,化简可得,则离心率.
方法二:因为焦点到渐近线的距离为,则有平行线的对应成比例可得知,即则离心率为. 选A.
3、利用双曲线方程求渐近线方程
【例6】【广东省珠海市2019届高三9月摸底考试】双曲线的渐近线为( )
A. B. C. D.
【答案】A
【解析】
【分析】
令双曲线方程右侧为零,即可求出渐近线方程.也可以根据双曲线的定义,确定,即可求出渐近线方程.
【点睛】
本题主要考查双曲线渐近线方程的求解,考查基本知识和基本计算能力.
类型三、求离心率的值或范围.
1、利用离心率定义求离心率
【例7】【清华大学中学生标准学术能力诊断性测试2018年11月测试(一卷)】已知,是双曲线的左、右焦点,点M在E上,与x轴垂直,,则E的离心率为( )学, , ]
A. B. C. D. 2
【答案】A
【解析】
【分析】
根据双曲线的定义,用a表示出,结合勾股定理和离心率的公式即可求得离心率。
【详解】
根据题意,做出图像如下图所示
因为 ,
设
由双曲线定义可知,即
在Rt△MF2F1中,由勾股定理可知
,即
联立方程得
化简得
所以选A
【点睛】
本题考查了双曲线定义及性质的简单应用,离心率的简单求法,属于基础题。
2、利用渐近线方程求离心率 学 ]
【例8】【河北省唐山市2018-2019学年高三上学期第一次摸底考试】双曲线的渐近线方程为,则的离心率为
A. 2 B. C. D.
【答案】C
【解析】
【分析】
由双曲线的方程的渐近线方程,求得,再由离心率的计算公式,即可求解.
【详解】
由题意,双曲线的渐近线方程为,
即,所以双曲线的离心率为,故选C.
【点睛】
本题主要考查了双曲线的几何性质,其中熟记双曲线的标准方程和简单的几何性质是解答的关键,着重考查了推理与运算能力,属于基础题.
类型四、求双曲线的方程
1. 利用双曲线的定义求其方程
【例9】【2017届上海市徐汇区高三下学期二模】过椭圆右焦点的圆与圆外切,则该圆直径的端点的轨迹是( )
A. 一条射线 B. 两条射线 C. 双曲线的一支 D. 抛物线
【答案】C
【解析】根据题意, ,所以焦点坐标,设过点的圆的圆心为,半径为,连结,如图:
因为圆与圆外切,所以,因为,所以,所以
,所以点在以为焦点的双曲线的右支上,故选
点睛:本题主要考查的是点轨迹问题,属于中等难度题。在判断点的轨迹时结合图像去寻找关系式。利用两个圆外切,圆心距等于两个半径之和,根据中位线定理,即可得到,结合双曲线的定义,所以点是双曲线的一支。
2.利用渐近线方程求双曲线方程
【例10】【湖南省长沙市长郡中学2017届高三下学期临考冲刺训练】已知双曲线
的左、右焦点分别为,两条渐近线分别为,过作于点,过作于点为原点,若是边长为的等边三角形,则双曲线的方程为( )
A. B. C. D.
【答案】C
方法、规律归纳:
1.求双曲线离心率的值
(1)直接求出,求解:已知标准方程或a,c易求时,可利用离心率公式e=求解;
(2)变用公式,整体求:如利用e===,e==;
2.双曲线的离心率与渐近线方程之间有着密切的联系,二者之间可以互求.已知渐近线方程时,可得的值,于是e2===1+2,因此可求出离心率e的值;而已知离心率的值,也可求出渐近线的方程,即=.但要注意,当双曲线的焦点所在的坐标轴不确定时,上述两类问题都有两个解.
实战演练:
1.【黑龙江省2018年普通高等学校招生全国统一考试仿真模拟(七)】若双曲线的顶点和焦点分别为椭圆的焦点和顶点,则该双曲线方程为( )
A. B. C. D.
【答案】A
【解析】
【分析】
首先确定椭圆的焦点和顶点,然后求解双曲线的方程即可.
【点睛】
求双曲线的标准方程的基本方法是待定系数法.具体过程是先定形,再定量,即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线之间的关系,求出a,b的值.如果已知双曲线的渐近线方程,求双曲线的标准方程,可利用有公共渐近线的双曲线方程为,再由条件求出λ的值即可.
2.【浙江省诸暨市2018届高三5月适应性考试】已知双曲线的一条渐近线截椭圆所得弦长为,则此双曲线的离心率为( )
A. B. C. D.
【答案】B
【解析】
【分析】
求出双曲线的渐近线方程.与椭圆的方程联立,利用弦长转化求解即可.
【详解】
双曲线的一条渐近线不妨设为: ,则: ,可得:
一条渐近线截椭圆所得弦长为,
可得:,可得 ,
解得 .
故选:B.
【点睛】
本题考查椭圆以及双曲线的简单性质的应用,考查转化思想以及计算能力.属中档题.
3.【河北省衡水中学2018届高三考前适应性训练】已知双曲线的虚轴长是实轴长的2倍,则双曲线的标准方程为( )
A. B. C. D.
【答案】D
【解析】
【分析】
利用双曲线方程求出实轴与虚轴长,列出方程求解即可.
【点睛】
本题考查双曲线的简单性质的应用,考查计算能力,属于基础题.
4.【山东省临沂市沂水县第一中学2018届高三第三轮考试】在双曲线中,称离心率等于的双曲线为黄金双曲线,则下列双曲线中,是黄金双曲线的为( )
A. B. C. D.
【答案】B
【解析】
【分析】
先求出每一个选项双曲线的离心率,再判断.
【点睛】
(1)本题主要考查双曲线的离心率的计算和双曲线的几何性质,意在考查学生对这些知识的掌握水平和计算能力.(2)计算本题时,可以直接计算离心率e,也可以计算,看是否等于
5.【宁夏银川市唐徕回民中学2018届高三下学期第四次模拟考】已知抛物线()与双曲线(,)有相同的焦点,点是两条曲线的一个交点,且轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. B. C. D.
【答案】B
【解析】
【详解】
分析:因为抛物线与双曲线有相同的焦点,所以可得p与c之间的关系,
因为轴,则点A的坐标可以由抛物线求出,将其代入双曲线方程,
再由a、b、c之间的关系,可求出离心率,由离心率公式可得,即斜率的值,由斜率求出倾斜角的范围.
详解:因为抛物线与双曲线焦点相同,所以,因为与x轴垂直,所以可求得点A的坐标为,将其代入双曲线方程可得:,
因为,代入上式可得:,
化简得:,两边同时除以得:,
解得或(舍),设渐近线斜率为k,
由,解得,所以倾斜角应大于,
所以区间可能是,
故选B.
点睛:本题主要考查抛物线与双曲线的几何性质,由焦点与公共点建立系数之间的联系,渐近线斜率与离心率有关,所以由系数求出离心率并求得斜率,与特殊倾斜角的斜率作对比,求出倾斜角取值范围.
6.【黑龙江省2018年普通高等学校招生全国统一考试仿真模拟(一)】当双曲线的焦距取得最小值时,其渐近线的斜率是( )
A. B. C. D.
【答案】B
【解析】
【分析】
由题意可得6﹣2m>0,即有m<3,由c2=m2+8+6﹣2m=(m﹣1)2+13,可得m=1取得最小值,由双曲线的渐近线方程,可得渐近线的斜率.
【点睛】 ]
本题考查双曲线的渐近线的斜率的求法,考查了二次函数的最值的求法,考查运算能力,属于中档题.
7.【四川省成都市第七中学2018届高三下学期三诊】已知双曲线的右顶点到其一条渐近线的距离等于,抛物线的焦点与双曲线的右焦点重合,则抛物线上的动点到直线和距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
分析:由双曲线的右顶点到渐近线的距离求出,从而可确定双曲线的方程和焦点坐标,进而得到抛物线的方程和焦点,然后根据抛物线的定义将点M到直线的距离转化为到焦点的距离,最后结合图形根据“垂线段最短”求解.
∴双曲线的方程为,
∴双曲线的焦点为.
又抛物线的焦点与双曲线的右焦点重合,
∴,
∴抛物线的方程为,焦点坐标为.如图,
设点M到直线的距离为,到直线的距离为,则,
∴.
结合图形可得当三点共线时,最小,且最小值为点F到直线的距离.
故选B.
点睛:与抛物线有关的最值问题一般情况下都与抛物线的定义有关,根据定义实现由点到点的距离与点到直线的距离的转化,具体有以下两种情形:
(1)将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”,使问题得解;
(2)将抛物线上的点到焦点的距离转化为点到准线的距离,利用“与直线上所有点的连线中的垂线段最短”解决.
8.【普通高等学校招生全国统一考试2018届高三下学期第二次调研考试】在下列双曲线方程中,表示焦点在y轴上且渐近线方程为的是
A. B. C. D.
【答案】C
9.【安徽省六安市第一中学2018届高三下学期适应性考试】已知双曲线的方程为,则下列关于双曲线说法正确的是( )
A. 虚轴长为 B. 焦距为
C. 离心率为 D. 渐近线方程为
【答案】D
【解析】
分析:根据题意,由双曲线的标准方程依次分析选项,综合即可得答案.
解析:根据题意,依次分析选项:
对于A,双曲线的方程为,其中b=3,虚轴长为6,则A错误;
对于B,双曲线的方程为,其中a=2,b=3,则,则焦距为,则B错误;
对于C,双曲线的方程为,其中a=2,b=3,则,则离心率为
,则C错误;
对于D,双曲线的方程为,其中a=2,b=3,则渐近线方程为,则D正确.
故选:D.
点睛:本题考查双曲线的标准方程,注意有双曲线的标准方程a、b的值.
10.【山东省潍坊市青州市2018届高三第三次高考模拟考试】已知双曲线的离心率为,且经过点,则双曲线的实轴长为( )
A. B. C. D.
【答案】C
【解析】分析:由题意双曲线的离心率为,得,把点,代入双曲线的方程,解得,即可得到答案.
点睛:本题主要考查了双曲线的标准方程及其简单的几何性质,其中熟记双曲线的几何性质是解答的关键,着重考查了推理与运算能力.
11.【辽宁省葫芦岛市2018年普通高中高三第二次模拟】已知双曲线,若过一、三象限的渐近线的倾斜角,则双曲线的离心率的取值范围是( )
A. B. C. D.
【答案】A
【解析】分析:求得双曲线的渐近线方程,由题意可得,再由离心率公式和 的关系,即可得到所求范围.
点睛:本题考查双曲线的方程和性质,主要考查渐近线方程的运用,考查运算能力,属于中档题.
12.【江西省抚州市临川区第一中学2018届高三全真模拟(最后一模)】已知定点,,是圆:上任意一点,点关于点的对称点为,线段的中垂线与直线相交于点,则点的轨迹是( )
A. 直线 B. 圆 C. 椭圆 D. 双曲线
【答案】D
【解析】分析:根据三角形中位线性质以及中垂线性质得,再根据双曲线定义得结果.
详解:因为N为中点,O为中点,所以
因为P在线段的中垂线上,所以
因此,即点的轨迹是双曲线,
选D.
点睛:求轨迹方程,一般有以下方法,一是定义法,动点满足圆或圆锥曲线定义;二是直接法,化简条件即得;三是转移法,除所求动点外,一般还有已知轨迹的动点,寻求两者关系是关键;四是交轨法或参数法,如何消去参数是解题关键,且需注意消参过程中的等价性.
13.【河南省巩义市市直高中2018届高三下学期模拟考试】已知,是双曲线的左、右焦点,过的直线与双曲线的左支交于点,与右支交于点,若,,则( )
A. B. C. D.
【答案】C
【解析】分析:先利用双曲线的定义求出,再利用余弦定理求出,再利用双曲线的定义判定为等边三角形,利用分割法和三角形的面积公式进行求解.
因为,
且, 学, , ,X,X,K]
所以,
又,
所以为等边三角形,
则
.
点睛:处理椭圆或双曲线上的点到焦点的距离时,往往利用椭圆或双曲线的定义合理转化,如本题中两次利用双曲线的定义,第一次是求得,第二次是结合、判定三角形的形状.
14.【河南省安阳35中2018届高三核心押题卷】若双曲线的左、右焦点分别为 是右支上的一点,与轴交于点,的内切圆在边上的切点为,若,则的离心率是( )
A. B. C. D.
【答案】A
【解析】分析:已知可得,故要求离心率只需求。设的内切圆在边上的切点分别为M、N。由内切圆的切线长线段可得。由双曲线的对称性可得。由双曲线的定义可得,根据以上结论可得。进而可求离心率。
点睛:求圆锥曲线的离心率,应从条件得到关于的关系式。解题过程注意的关系。
(1)直接根据题意建立的等式求解; 学 ]
(2)借助平面几何关系建立的等式求解;
(3)利用圆锥曲线的相关细则建立的等式求解;
(4)运用数形结合建立的等式求解;
15.【河南省南阳市第一中学2018届高三第十八次考试】已知为双曲线上的任意一点,过分别引其渐近线的平行线,分别交轴于点,交轴于点,若恒成立,则双曲线离心率的取值范围为( )
A. B. C. D.
【答案】B
【解析】分析:设,表示出渐近线方程,求出和,建立a, b,c之间的关系。
令x=0,得,令y=0得
据此有
恒成立,则恒成立,
,则即
可得
故选B.
点睛:本题主要考查双曲线的渐近线方程和离心率的综合应用,难度较大。