陕西省西安中学2019-2020学年高一下学期期中考试数学（实验班）试卷

陕西省西安中学2019-2020学年高一下学期期中考试数学（实验班）试卷

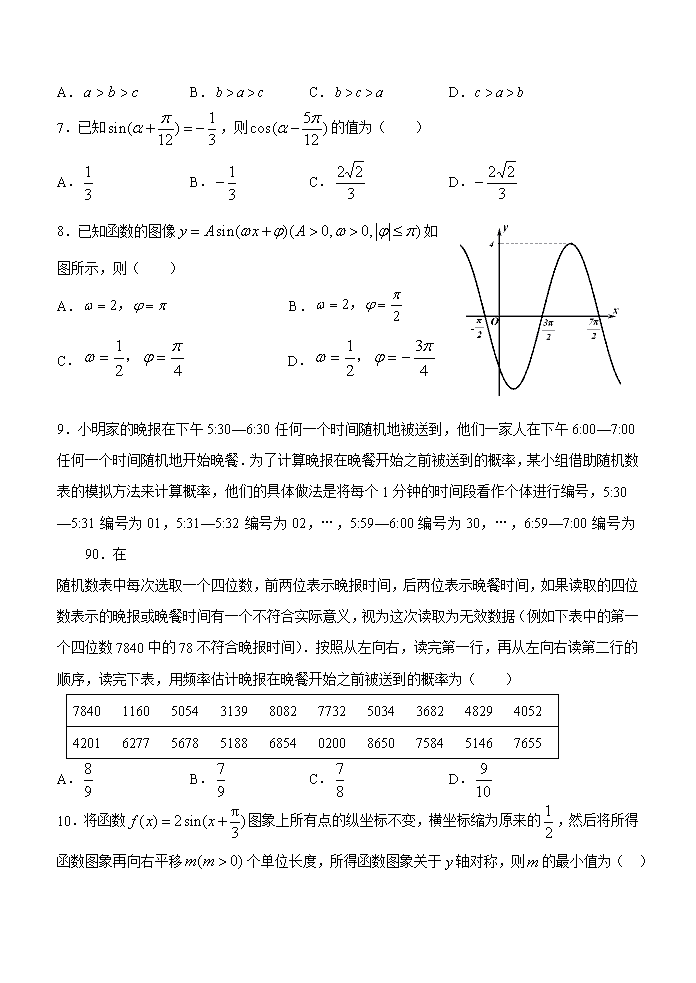
西安中学2019—2020学年度第二学期期中考试 高一数学（实验班）试题 ‎（时间：120分钟 满分：120分） 命题人： ‎ 一、选择题：(本题共10小题，每题4分，共40分．每题有且只有一个正确答案, 直接将答案填写在指定位置)‎ ‎1．为了解1000名学生的学习情况，采用系统抽样的方法，从中抽取容量为25的样本，则分组数和分段的间隔分别为（ ）‎ A．50，20 B．40，25 C．25，40 D．20，50‎ ‎2．从装有红球、白球和黑球各2个的口袋内一次取出2个球，则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一个白球；③两球至多有一个白球”中的哪几个（ ）‎ A．①② B．①③ C．②③ D．①②③‎ ‎3．设函数，则函数的最大值及取到最大值时的x取值集合分别为（ ）‎ A．3， B．1， ‎ C．3， D．1，‎ ‎4．在区间上随机取一个数x，的值介于到1之间的概率为（ ）‎ A． B． C． D． ‎ ‎5．下列既是偶函数又是以为周期的函数（ ）‎ A． B．　‎ C． D．‎ ‎6．设，，，则（ ）‎ A． B． C． D．‎ ‎7．已知，则的值为（ ）‎ A． B． C． D．‎ ‎8．已知函数的图像如图所示，则（ ）‎ A． B． ‎ C． D． ‎ ‎9．小明家的晚报在下午5:30—6:30任何一个时间随机地被送到，他们一家人在下午6:00—7:00‎ 任何一个时间随机地开始晚餐．为了计算晚报在晚餐开始之前被送到的概率，某小组借助随机数 表的模拟方法来计算概率，他们的具体做法是将每个1分钟的时间段看作个体进行编号，5:30‎ ‎—5:31编号为01，5:31—5:32编号为02，…，5:59—6:00编号为30，…，6:59—7:00编号为90．在 随机数表中每次选取一个四位数，前两位表示晚报时间，后两位表示晚餐时间，如果读取的四位 数表示的晚报或晚餐时间有一个不符合实际意义，视为这次读取为无效数据（例如下表中的第一 个四位数7840中的78不符合晚报时间）．按照从左向右，读完第一行，再从左向右读第二行的 顺序，读完下表，用频率估计晚报在晚餐开始之前被送到的概率为（ ）‎ ‎7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 ‎ ‎4201 6277 5678 5188 6854 0200 8650 7584 5146 7655‎ A． B． C． D．‎ ‎10．将函数图象上所有点的纵坐标不变，横坐标缩为原来的，然后将所得函数图象再向右平移个单位长度，所得函数图象关于轴对称，则的最小值为（ ）‎ A． B． C． D．‎ 二、填空题：（本题共5小题，每题4分，共20分, 直接将答案填写在指定位置）‎ ‎11． _______________．‎ ‎12．用长的铁丝围成一个扇形，则围成扇形的最大面积为_______________． ‎ ‎13．已知样本的平均数为，且，则此样本的方差为_____________．‎ ‎14．已知，，则的值为_______．‎ ‎15．如图所示的茎叶图是甲、乙两个代表队各7名队员参加“安全知识竞赛”的成绩，乙队成绩的众数为，从甲、乙两队中各选取1名队员，则两名队员所得分数相同的概率为 ． ‎ 三、解答题：（本题共5小题，每题12分，共60分．解答应写出必要的文字说明，证明过程或演算步骤，在答题卷中相应位置作答）‎ ‎16．计算（本小题满分12分）‎ ‎（1）已知均为锐角，，角的顶点是直角坐标系的原点，始边与轴的非负半轴重合，终边上有一点， 求；‎ ‎（2）已知，且，求． ‎ ‎17．（本小题满分12分）某校为了解本校学生网课期间课后玩电脑游戏时长情况，随机抽取了100名学生进行调查．下面是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图．‎ ‎（1）根据频率分布直方图估计抽取样本的平均数（同一组中的数据用该组区间的中点值作代表）；‎ ‎（2）已知样本中玩电脑游戏时长在的学生中，男生比女生多1人，现从中任选人进行回访，求选出的3人中恰有两人是男生的概率．‎ ‎18．（本小题满分12分）已知函数 ‎．‎ ‎（1）求函数的最小正周期、单调递增区间；‎ ‎（2）求在区间上的值域．‎ ‎19．（本小题满分12分）下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) ．‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎70‎ ‎65‎ ‎55‎ ‎38‎ ‎22‎ ‎（1）若y与x有较强的线性相关关系，根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程；‎ ‎（2）若该农产品每吨的成本为13.1千元，假设该农产品可全部卖出，利用上问所求的回归方程，预测当年产量为多少吨时，年利润Z最大？‎ ‎（参考公式：回归直线方程为，其中）‎ ‎20．（本小题满分12分）已知函数，．‎ ‎（1）求函数的值域；‎ ‎（2）求不等式的解集；‎ ‎（3）若关于x的方程在恰有4个不同的解，求k的取值范围．（直接给出答案，不用书写解答过程）．‎