北京市第十四中学2021届高三第一学期期中考试数学试卷

北京市第十四中学2021届高三第一学期期中考试数学试卷

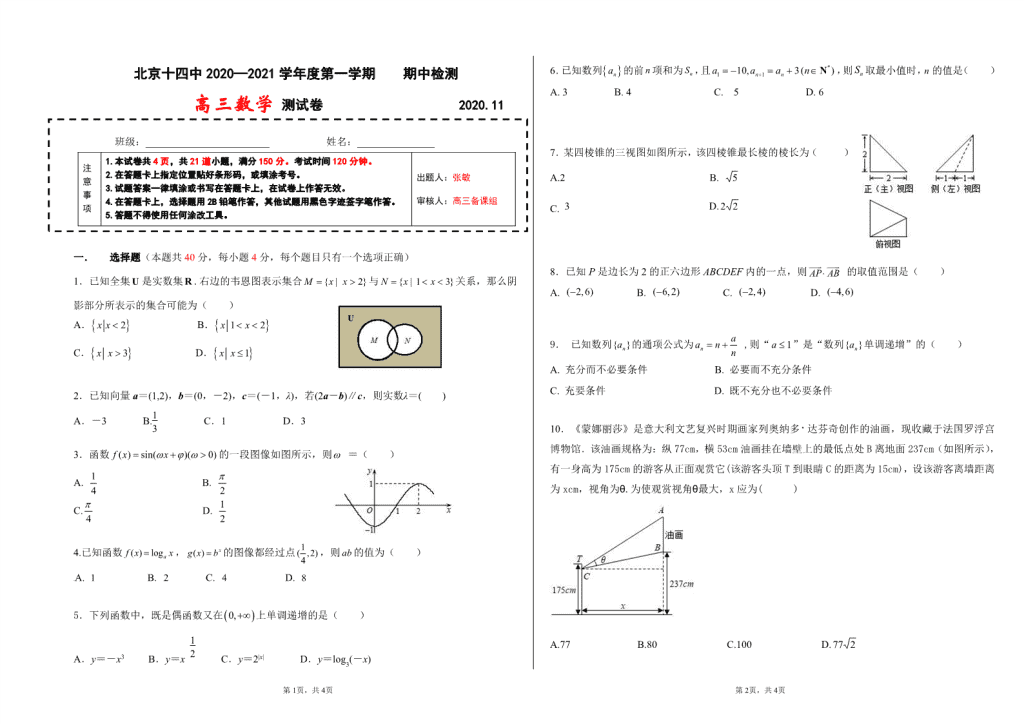
第 1页，共 4页 第 2页，共 4页 北京十四中 2020—2021 学年度第一学期 期中检测 高三数学 测试卷 2020.11 班级：________________________ 姓名：_______________ 一． 选择题（本题共 40 分，每小题 4 分，每个题目只有一个选项正确） 1．已知全集 U 是实数集R .右边的韦恩图表示集合 { | 2}M x x  与 { | 1 3}N x x   关系，那么阴 影部分所表示的集合可能为（ ） A． 2x x  B． 1 2x x  C． 3x x  D． 1x x  2．已知向量 a＝(1,2)，b＝(0，－2)，c＝(－1，λ)，若(2a－b)∥c，则实数λ＝( ) A．－3 B.1 3 C．1 D．3 3．函数 ( ) sin( )( 0)f x x     的一段图像如图所示，则 ＝（ ） A. 4 1 B. 2  C. 4  D. 2 1 4.已知函数 ( ) logaf x x ， ( ) xg x b 的图像都经过点 1( ,2)4 ，则 ab 的值为（ ） A. 1 B. 2 C. 4 D. 8 5．下列函数中，既是偶函数又在 0, 上单调递增的是（ ） A．y＝－x3 B．y＝x 1 2 C．y＝2|x| D．y＝log3(－x) 6．已知数列 na 的前 n 项和为 nS ，且 * 1 110, 3( )n na a a n    N ，则 nS 取最小值时，n 的值是（ ） A. 3 B. 4 C. 5 D. 6 7．某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（ ） A.2 B. 5 C. 3 D. 22 8．已知 P 是边长为 2 的正六边形 ABCDEF 内的一点，则 AP AB  的取值范围是（ ） A. ( )2,6 B. ( 6,2) C. ( 2,4) D. ( 4,6) 9． 已知数列 }{ na 的通项公式为 n anan  ,则“ 1a ”是“数列 }{ na 单调递增”的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 10．《蒙娜丽莎》是意大利文艺复兴时期画家列奥纳多 达芬奇创作的油画，现收藏于法国罗浮宫 博物馆．该油画规格为：纵 77cm，横 53cm 油画挂在墙壁上的最低点处 B 离地面 237cm（如图所示）， 有一身高为 175cm 的游客从正面观赏它(该游客头顶 T 到眼睛 C 的距离为 15cm)，设该游客离墙距离 为 xcm，视角为θ.为使观赏视角θ最大，x 应为( ) A.77 B.80 C.100 D. 277 注 意 事 项 1.本试卷共 4 页，共 21 道小题，满分 150 分。考试时间 120 分钟。 2.在答题卡上指定位置贴好条形码，或填涂考号。 3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。 4.在答题卡上，选择题用 2B 铅笔作答，其他试题用黑色字迹签字笔作答。 5.答题不得使用任何涂改工具。 出题人：张敏 审核人：高三备课组 第 3页，共 4页 第 4页，共 4页 二． 填空题（本题共 25 分，每小题 5 分） 11．角 的终边经过点 )3,1( P ，则  )6sin(  . 12．已知 AB  ， AC  是不共线的两个向量， BE  1 2 AC  AB ，则 AE AC   . 13．函数 2 2, 0,( ) 3, 0 x xf x x x      ，满足 0( ) 1f x  的 0x 的取值范围是 . 14．在△ABC 中， 3AB ， 4AC ．若△ABC 的面积为 33 ，则 BC 的长是 . 15．给定函数 ( )y f x ，设集合 { | ( )}A x y f x  ， { | ( )}B y y f x  ．若对于 x A  ， y B  ，使得 0x y  成立，则称函数 ( )f x 具有性质 P ．给出下列三个函数： ① 1y x  ； ② 1( )2 xy  ； ③ lgy x ． 其中，具有性质 P 的函数的序号是 . 三． 解答题（本题共 85 分） 16．（本小题 14 分）已知等差数列{an}和等比数列{bn}满足 a1＝b1＝1，a2＋a4＝10，b2b4＝a5. (Ⅰ)求{an}的通项公式； (Ⅱ)若 a1＋a2＋a3＋…＋an =81，求 n; (Ⅲ)求和：b1＋b3＋b5＋…＋b2n－1． 17．（本小题 14 分）已知函数 2 1( ) (2cos 1)sin 2 cos42f x x x x   ． （Ⅰ）求 ( )f x 的最小正周期； （Ⅱ）求 ( )f x 的最大和最小值以及相应的 x 的取值； (Ⅲ)若 π( , π)2   ，且 4 2)( f ，求 的值． 18．（本小题 14 分）已知函数 f(x)＝(x2＋ax＋a)ex(a≤2，x∈R)． (Ⅰ)当 a＝1 时，求 f(x)的单调区间； (Ⅱ)是否存在实数 a，使 f(x)的极大值为 3；若存在，求出 a 的值，若不存在，请说明理由． 19. （ 本 小 题 15 分 ） 在 四 棱 锥 P ABCD 中 ， 平 面 PAD  平 面 ABCD ， PAD 为 等 边 三 角 形, 1 2AB AD CD  , AB AD , //AB CD ,点 M 是 PC 的中点． （I）求证: //MB 平面 PAD ； （II）求二面角 P BC D  的余弦值； （III）在线段 PB 上是否存在点 N ，使得 DN 平面 PBC ？若存在,请求出 PN PB 的值；若不存在,请说明理由. 20.（本小题14分）已知函数 )12)(1()(  xaaxexf x . (Ⅰ)若 1a ，求函数 )(xf 的图像在点 ))0(,0( f 处的切线方程； (Ⅱ)当 0x 时，函数 0)( xf 恒成立，求a 的取值范围. 21.（本小题 14 分）已知任意的正整数 n 都可唯一表示为 1 1 0 0 1 12 2 2 2k k k kn a a a a          ，其中 0 1a  ， 1 2, , , {0,1}ka a a  ， *Nk  ．对于 n N ，数列{ }nb 满足：当 0 1, , , ka a a 中有偶数个 1 时， 0nb  ；否则 1nb  ．如 数 5 可以唯一表示为 2 1 05 1 2 0 2 1 2      ，则 5 0b  ． （Ⅰ）写出数列{ }nb 的前 8 项； （Ⅱ）求证：数列{ }nb 中连续为 1 的项不超过 2 项； （Ⅲ）记数列{ }nb 的前 n 项和为 nS ，求满足 1026nS  的所有 n 的值．（结论不要求证明）