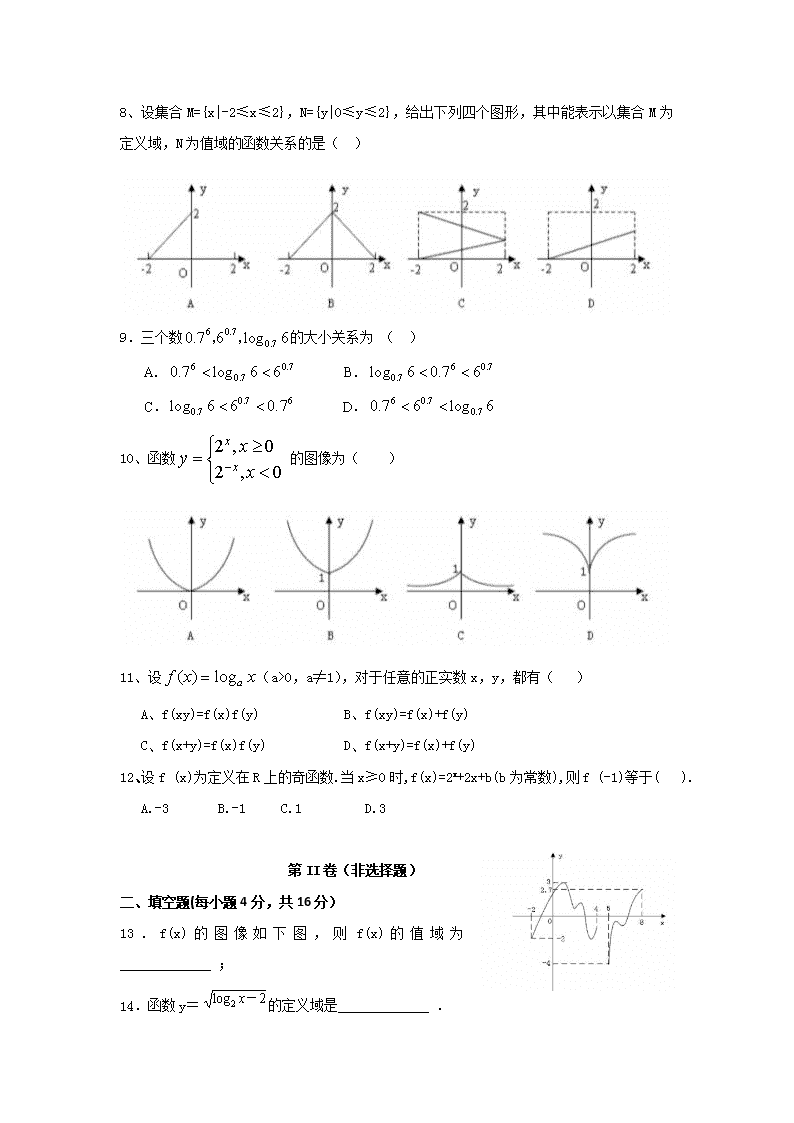
2018-2019学年西藏自治区林芝市第二高级中学高一上学期期中考试数学试题
2018-2019学年西藏自治区林芝市第二高级中学高一上学期期中考试数学试题
第I卷(选择题)
一、选择题(每小题4分,共48分)
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩B=( )
A.{3,5} B.{3,6} C.{3,7} D.{3,9}
2.设集合A={x|2≤x<4},B={x|3x-7≥8-2x},则A∪B等于( )
A.{x|x≥3} B.{x|x≥2} C.{x|2≤x<3} D.{x|x≥4}
3.已知集合A={x|x>0},B={x|-1≤x≤2},则A∪B=( )
A.{x|x≥-1} B.{x|x≤2 } C.{x|0
0,a≠1),对于任意的正实数x,y,都有( )
A、f(xy)=f(x)f(y) B、f(xy)=f(x)+f(y)
C、f(x+y)=f(x)f(y) D、f(x+y)=f(x)+f(y)
12、设f (x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f (-1)等于( ).
A.-3 B.-1 C.1 D.3
第II卷(非选择题)
二、填空题(每小题4分,共16分)
13.f(x)的图像如下图,则f(x)的值域为 _____________ ;
14.函数y=的定义域是_____________ .
15.满足{1,3}∪A={1,3,5}的所有集合A的个数是________.
16、已知幂函数的图象经过点(3,),那么这个幂函数的解析式为_____________.
三、解答题(共70分)
17.(本题6分)设,,
求:(1);(2)
18、(本题10分)设全集为R,,,求及
19. 若集合,且,求实
数的值;
20、(本题6分)计算下式的值
(1)
21、(本题6分)计算下式的值
(1)
22、(6)已知
(Ⅰ)证明函数f ( x )的图象关于轴对称;
(Ⅱ)判断在上的单调性,并用定义加以证明;
(Ⅲ)当x∈[-2,-1]时函数f (x )的最大值为,求此时a的值.
2018-2019学年第一学期林芝市二高期中数学试卷 答案
一、选择题(每小题4分,共48分)
1.D,2.B,3.A,4.A,5.D,6.A,7.C,8.B,9.B,10.B,11.B,12.A
二、填空题(每小题4分,共16分)
13.13、[-4,3] 14、{x|x≥4} 15.4; 16.
三、解答题(共36分)
17(6分)解:
(1)又
(2)又得
18、 解:
19.解:由;因此,
(i)若时,得,此时,;
(ii)若时,得,此时,;
(iii)若且时,得,此时,不是的子集;
20、解(1)原式=
=
=
=
21、原式=
=
=
22、解:(Ⅰ)要证明函数f ( x )的图象关于轴对称则只须证明函数f ( x )是偶函数…1分
∵x∈R …………
由 …………
∴函数f ( x )是偶函数,即函数f ( x )的图象关于轴对称…………
(Ⅱ)证明:设,则………6分
=
由a>1 且 0<,则x1+x2>0,、、、;
<0即;
所以, f(x)在上都为增函数.………………………
(Ⅲ)由(Ⅰ)Ⅱ)知f(x) 是偶函数且在上为增函数,则知f(x)在上为减函数;
则当x∈[-2,-1]时,函数f (x )为减函数
由于函数f(x)的最大值为,则f(-2)=
即,解得,或 ……………………….