高一数学（人教A版）必修4能力提升：1-5-2 函数y＝Asin(ωx＋φ)的性质及应用

高一数学（人教A版）必修4能力提升：1-5-2 函数y＝Asin(ωx＋φ)的性质及应用

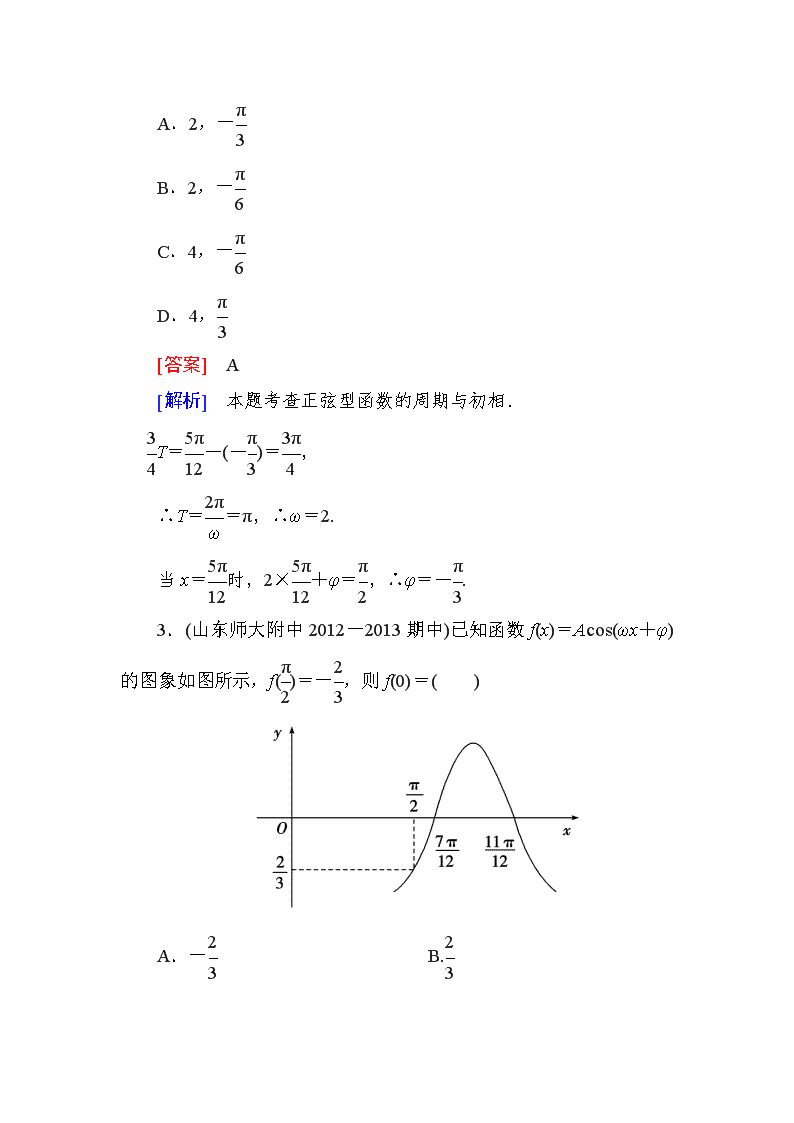
能 力 提 升 一、选择题 ‎1．已知函数f(x)＝sin(ωx＋)(ω>0)的最小正周期为π，则该函数图象(　　)‎ A．关于点对称 B．关于直线x＝对称 C．关于点对称 D．关于直线x＝对称 ‎[答案]　A ‎[解析]　由T＝＝π，解得ω＝2，‎ 则f(x)＝sin，‎ 则该函数图象关于点对称．‎ ‎2．(2013·四川理)函数f(x)＝2sin(ωx＋φ)(ω>0，－<φ<)的部分图象如图所示，则ω、φ的值分别是(　　)‎ A．2，－ B．2，－ C．4，－ D．4， ‎[答案]　A ‎[解析]　本题考查正弦型函数的周期与初相．‎ T＝－(－)＝，‎ ‎∴T＝＝π，∴ω＝2.‎ 当x＝时，2×＋φ＝，∴φ＝－.‎ ‎3．(山东师大附中2012－2013期中)已知函数f(x)＝Acos(ωx＋φ)的图象如图所示，f()＝－，则f(0)＝(　　)‎ A．－　　　 B.　　　‎ C．－　　　 D. ‎[答案]　B ‎[解析]　首先由图象可知所求函数的周期为 T＝2＝，故ω＝＝3.‎ 将代入解析式，‎ 得Acos＝0，即cos＝0，‎ ‎∴＋φ＝＋2kπ，k∈Z，‎ ‎∴φ＝－＋2kπ(k∈Z)．‎ 令φ＝－，代入解析式得f(x)＝Acos.‎ 又∵f＝－，‎ ‎∴f＝－Asin＝－A＝－，‎ ‎∴A＝，‎ ‎∴f(0)＝cos＝cos＝.‎ ‎4．(2011～2012·安徽合肥一模)已知函数f(x)＝2sin(ωx＋φ)(ω>0)的图象关于直线x＝对称，且f＝0，则ω的最小值为(　　)‎ A．2　　　　B．‎4　‎　　　C．6　　　　D．8‎ ‎[答案]　A ‎[解析]　函数f(x)的周期T≤4＝π，‎ 则≤π，解得ω≥2，故ω的最小值为2.‎ ‎5．若函数f(x)＝3sin(ωx＋φ)对任意x都有f＝f(－x)，则f＝(　　)‎ A．3或0 B．－3或3‎ C．0 D．－3或0‎ ‎[答案]　B ‎[解析]　由于函数f(x)＝3sin(ωx＋φ)对任意x都有f＝f(－x)，‎ 则函数f(x)的图象关于直线x＝对称，‎ 则f是函数f(x)的最大值或最小值，‎ 则f＝－3或3.‎ ‎6．若函数f(x)＝2sin是偶函数，则φ的值可以是(　　)‎ A.　　　 B.　　　‎ C.　　　 D．－ ‎[答案]　A ‎[解析]　由于f(x)是偶函数，‎ 则f(x)图象关于y轴即直线x＝0对称，‎ 则f(0)＝±2，‎ 又当φ＝时，f(0)＝2sin＝2，‎ 则φ的值可以是.‎ 二、填空题 ‎7．简谐振动s＝3sin，在t＝时的位移s＝________.初相φ＝________.‎ ‎[答案]　， ‎[解析]　当t＝时，s＝3sin＝3×＝.‎ ‎8．(山东济南一中12－13期中)已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)的图象如图所示，f(x)＝____________.‎ ‎[答案]　3sin(＋)‎ ‎[解析]　由图易知A＝3‎ 而＝－π＝2π 故T＝4π.ω＝＝ ‎∴f(x)＝3sin(＋φ)代入(π，3)‎ 得sin(＋φ)＝1‎ ‎∴＋φ＝解得φ＝ ‎∴f(x)＝3sin(＋)．‎ ‎9．(2013·长沙模拟)若将函数y＝sin(ωx＋)(ω>0)的图象向右平移个单位长度后，与函数y＝sin(ωx＋)的图象重合，则ω的最小值为________．‎ ‎[答案]　 ‎[解析]　y＝sin(ωx＋)的图象向右平移个单位后得到y＝sin[ω(x－)＋π]‎ 即y＝sin(ωx＋π－π)‎ 故π－π＋2kπ＝(k∈Z)‎ 即π＝π＋2kπ ω＝＋6k(k∈Z)‎ ‎∵ω>0，∴ω的最小值为.‎ 三、解答题 ‎10．(2011～2012·黑龙江高一检测)已知函数y＝Asin(ωx＋φ)(A，ω>0且|φ|<π)在一个周期内的图象如图，‎ ‎(1)求函数的解析式．‎ ‎(2)求函数的单调递增区间．‎ ‎[解析]　(1)由图得A＝2，T＝2[－(－)]＝π，‎ ω＝＝＝2，‎ 故y＝2sin(2x＋φ)．‎ 又2sin(－2×＋φ)＝2，即sin(－＋φ)＝1，‎ ‎∴φ＝2kπ＋，k∈Z，又|φ|<π，∴φ＝ 得函数解析式为y＝2sin(2x＋)．‎ ‎(2)令z＝2x＋，函数y＝sinz的单调递增区间是 ‎[－＋2kπ，＋2kπ](k∈Z)‎ 由－＋2kπ≤2x＋≤＋2kπ 得－＋kπ≤x≤－＋kπ(k∈Z)‎ 所以函数y＝2sin(2x＋)的递增区间为[－＋kπ，－＋kπ]，k∈Z.‎ ‎11．已知函数f(x)＝sin(ωx＋φ)(ω>0,0≤φ≤π)是R上的偶函数，其图象关于点M对称，且在区间上是单调函数，求ω和φ的值．‎ ‎[解析]　∵f(x)＝sin(ωx＋φ)是R上的偶函数，‎ ‎∴φ＝＋kπ，k∈Z.‎ 又∵0≤φ≤π，∴φ＝，‎ ‎∴f(x)＝sin＝cosωx.‎ ‎∵图象关于点对称，∴cosω＝0.‎ ‎∴ω＝＋nπ，n∈Z.∴ω＝＋n，n∈Z.‎ 又∵f(x)在区间上是单调函数，∴≥－0，‎ 即×≥，∴ω≤2.‎ 又∵ω>0，∴ω＝或ω＝2.‎ ‎12．已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，－π<φ<0)，图象最低点的纵坐标是－，相邻的两个对称中心是和.‎ 求：(1)f(x)的解析式；‎ ‎(2)f(x)的值域；‎ ‎(3)f(x)的对称轴．‎ ‎[解析]　(1)A＝，T＝2＝π ‎∴＝π.∴ω＝2.∴f(x)＝sin(2x＋φ)．‎ 又在f(x)图象上，‎ ‎∴f＝0.∴sin＝0.‎ ‎∴sin＝0.‎ 又－π<φ<0，∴φ＝－.‎ ‎∴f(x)＝sin.‎ ‎(2)值域是[－，]．‎ ‎(3)令2x－＝＋kπ(k∈Z)，‎ ‎∴x＝＋(k∈Z)．‎ ‎∴对称轴是直线x＝＋(k∈Z)．‎