2020届二轮复习空间几何体的三视图、表面积与体积课时作业（全国通用）

2020届二轮复习空间几何体的三视图、表面积与体积课时作业（全国通用）

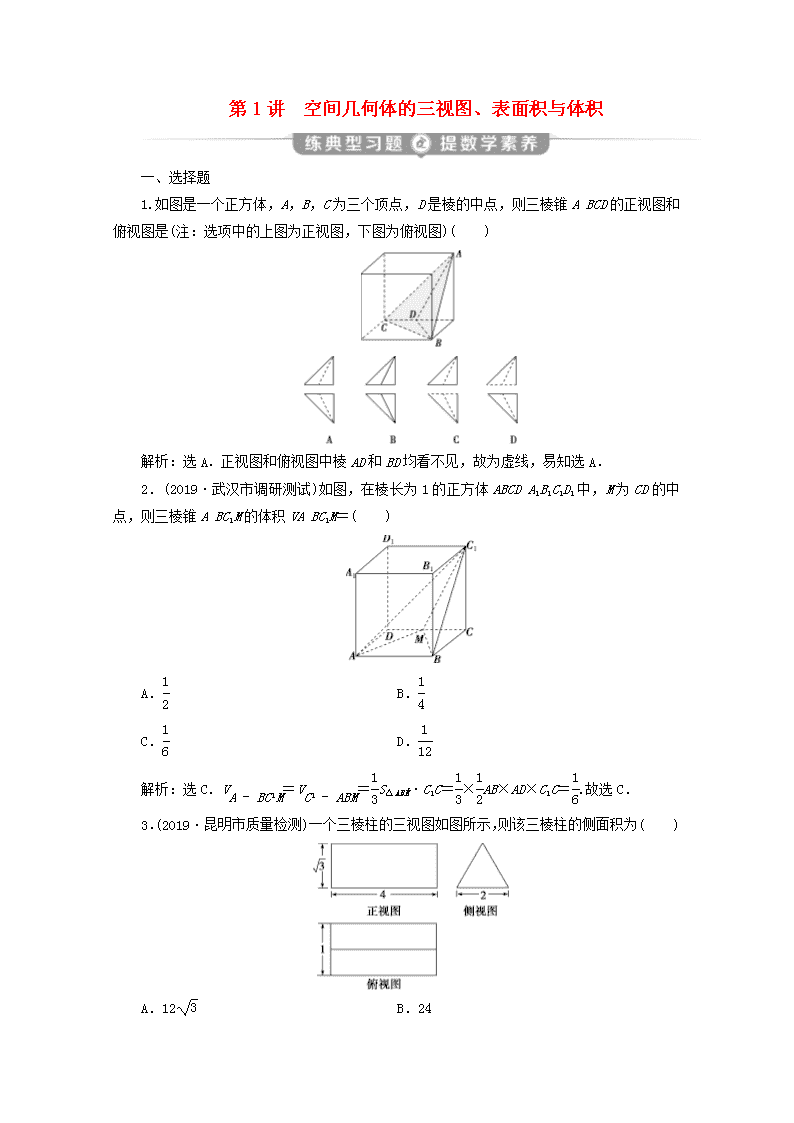
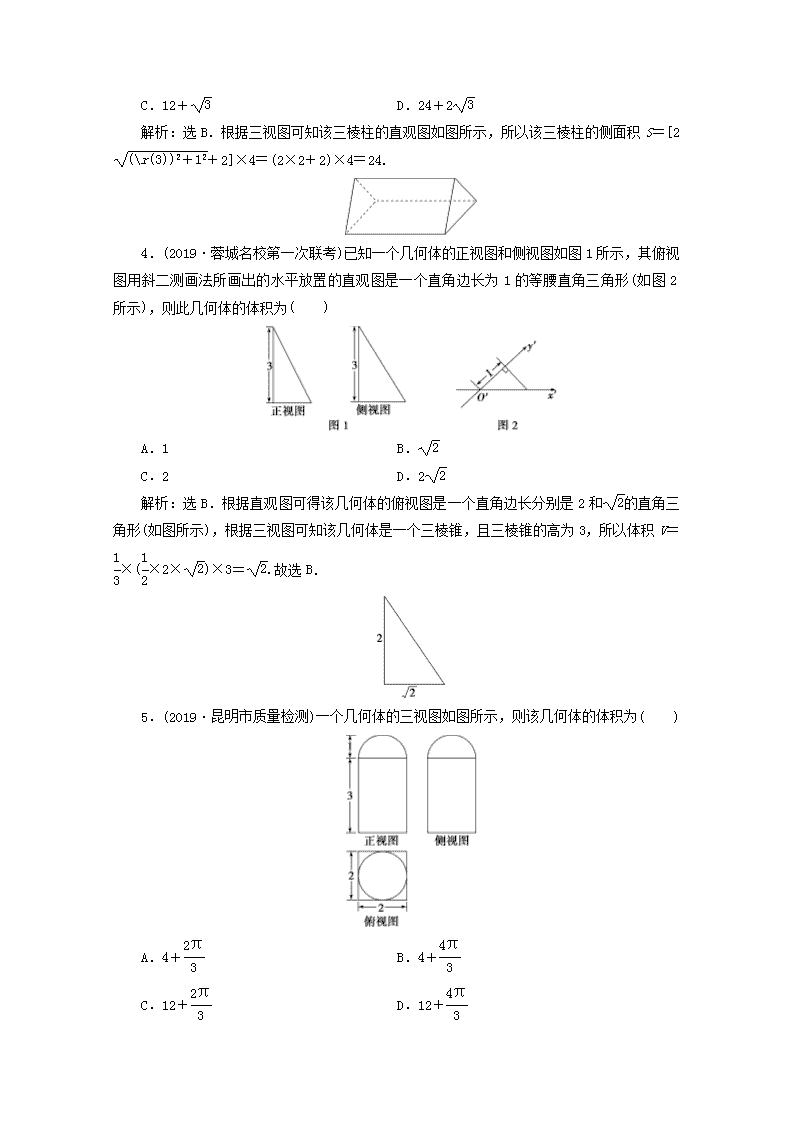
第1讲　空间几何体的三视图、表面积与体积 一、选择题 ‎1.如图是一个正方体，A，B，C为三个顶点，D是棱的中点，则三棱锥ABCD的正视图和俯视图是(注：选项中的上图为正视图，下图为俯视图)(　　)‎ 解析：选A．正视图和俯视图中棱AD和BD均看不见，故为虚线，易知选A．‎ ‎2．(2019·武汉市调研测试)如图，在棱长为1的正方体ABCDA1B1C1D1中，M为CD的中点，则三棱锥ABC1M的体积VABC1M＝(　　)‎ A．　　　　　　　　　 B． C． D． 解析：选C．V＝V＝S△ABM·C1C＝×AB×AD×C1C＝.故选C．‎ ‎3．(2019·昆明市质量检测)一个三棱柱的三视图如图所示，则该三棱柱的侧面积为(　　)‎ A．12 B．24‎ C．12＋ D．24＋2 解析：选B．根据三视图可知该三棱柱的直观图如图所示，所以该三棱柱的侧面积S＝[2＋2]×4＝(2×2＋2)×4＝24.‎ ‎4．(2019·蓉城名校第一次联考)已知一个几何体的正视图和侧视图如图1所示，其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图2所示)，则此几何体的体积为(　　)‎ A．1 B． C．2 D．2 解析：选B．根据直观图可得该几何体的俯视图是一个直角边长分别是2和的直角三角形(如图所示)，根据三视图可知该几何体是一个三棱锥，且三棱锥的高为3，所以体积V＝×(×2×)×3＝.故选B．‎ ‎5．(2019·昆明市质量检测)一个几何体的三视图如图所示，则该几何体的体积为(　　)‎ A．4＋ B．4＋ C．12＋ D．12＋ 解析：选C．三视图对应的几何体是一个半球与一个长方体的组合体，半球的半径为1，体积为，长方体的长、宽、高分别为2、2、3，体积为12.所以组合体的体积为12＋.故选C．‎ ‎6．(2019·合肥市第二次质量检测)如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中俯视图由两个半圆和两条线段组成，则该几何体的表面积为(　　)‎ A．17π＋12 B．12π＋12‎ C．20π＋12 D．16π＋12‎ 解析：选C．由三视图知，该几何体是一个由大半圆柱挖去一个小半圆柱得到的，两个半圆柱的底面半径分别为1和3，高均为3，所以该几何体的表面积为×2π×3×3＋×2π×1×3＋2×＋2×2×3＝20π＋12，故选C．‎ ‎7．(2019·济南市学习质量评估)某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A．5 B． C．6 D．8‎ 解析：选C．该几何体是以左视图为底面的五棱柱，高为2，底面积为2×1＋×2×1＝3，故其体积为3×2＝6.‎ ‎8．(2019·江西七校第一次联考)一个半径为1的球对称削去了三部分，其俯视图如图所示，那么该立体图形的表面积为(　　)‎ A．3π B．4π C．5π D．6π 解析：选C．由题中俯视图可知该球被平均分成6部分，削去了3部分，剩余的3部分为该几何体，所以该立体图形的表面积为2×π×12＋3×π×12＝5π，故选C．‎ ‎9．(2019·广州市综合检测(一))一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为(　　)‎ A． B．7π C． D．8π 解析：选B．由三视图可知该几何体是一个圆柱体和一个球体的四分之一的组合体，则所求的几何体的表面积为×4π×12＋π×12＋π×12＋2π×1×2＝7π，选B．‎ ‎10．(2019·重庆市七校联合考试)已知正三棱锥的高为6，内切球(与四个面都相切)的表面积为16π，则其底面边长为(　　)‎ A．18 B．12‎ C．6 D．4 解析：选B．由题意知，球心在三棱锥的高PE上，设内切球的半径为R，则S球＝4πR2＝16π，所以R＝2，所以OE＝OF＝2，OP＝4.在Rt△OPF中，PF＝＝2.因为△OPF∽△DPE，所以＝，得DE＝2，AD＝3DE＝6，AB＝AD＝12.故选B．‎ ‎11．(2019·福州市质量检测)如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为(　　)‎ A．32 B．16‎ C． D． 解析：选D．由三视图知，该几何体为直三棱柱ABCA1B1C1割去一个小三棱锥DABC后剩余的部分，如图所示，故所求几何体的体积为×43－××42×2＝.故选D．‎ ‎12．(2018·高考全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为(　　)‎ A． B． C． D． 解析：选A．记该正方体为ABCDA′B′C′D′，正方体的每条棱所在直线与平面α所成的角都相等，即共点的三条棱A′A，A′B′，A′D′与平面α所成的角都相等．如图，连接AB′，AD′，B′D′，因为三棱锥A′AB′D′是正三棱锥，所以A′A，A′B′，A′D′与平面AB′D′所成的角都相等．分别取C′D′，B′C′，BB′，AB，AD，DD′的中点E，F，G，H，I，J，连接EF，FG，GH，IH，IJ，JE，易得E，F，G，H，I，J六点共面，平面EFGHIJ与平面AB′D′平行，且截正方体所得截面的面积最大．又EF＝FG＝GH＝IH＝IJ＝JE＝，所以该正六边形的面积为6××＝，所以α截此正方体所得截面面积的最大值为，故选A．‎ 二、填空题 ‎13．(一题多解)(2019·南昌市第一次模拟测试)底面边长为6，侧面为等腰直角三角形的正三棱锥的高为________．‎ 解析：法一：由题意得，三棱锥的侧棱长为3，设正三棱锥的高为h，则××3×3×3＝××36h，解得h＝.‎ 法二：由题意得，三棱锥的侧棱长为3，底面正三角形的外接圆的半径为2，所以正三棱锥的高为＝.‎ 答案： ‎14．(2019·高考全国卷Ⅰ)已知∠ACB＝90°，P为平面ABC外一点，PC＝2，点P到∠ACB两边AC，BC的距离均为，那么P到平面ABC的距离为____________．‎ 解析：如图，过点P分别作PE⊥BC交BC于点E，作PF⊥AC交AC于点F.由题意知PE＝PF＝.过P作PH⊥平面ABC于点H，连接HE，HF，HC，易知HE＝HF，则点H在∠ACB的平分线上，又∠ACB＝90°，故△CEH为等腰直角三角形．在Rt△PCE中，PC＝2，PE＝，则CE＝1，故CH＝，在Rt△PCH中，可得PH＝，即点P到平面ABC的距离为.‎ 答案： ‎15．(2019·高考天津卷)已知四棱锥的底面是边长为的正方形，侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为________．‎ 解析：由题可得，四棱锥底面对角线的长为2，则圆柱底面的半径为，易知四棱锥的高为＝2，故圆柱的高为1，所以圆柱的体积为π××1＝.‎ 答案： ‎16. (2017·高考全国卷Ⅰ)如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为________．‎ 解析：由题意可知，折起后所得三棱锥为正三棱锥，当△ABC的边长变化时，设△ABC的边长为a(a>0)cm，则△ABC的面积为a2，△DBC的高为5－a，则正三棱锥的高为＝，所以25－a>0，所以0

查看更多