2021届新高考版高考数学一轮复习课件：§3-3　二次函数与幂函数（讲解部分）

2021届新高考版高考数学一轮复习课件：§3-3　二次函数与幂函数（讲解部分）

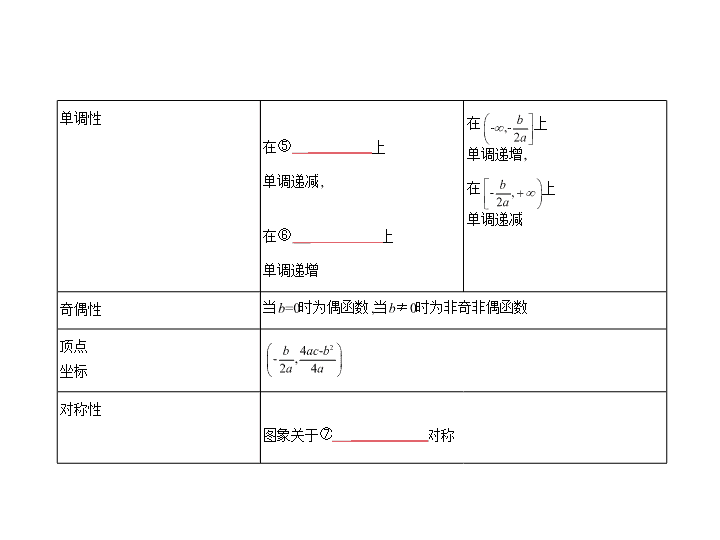
考点一　二次函数的图象与性质 1.二次函数的解析式 (1)一般式: f ( x )= ax 2 + bx + c ( a ≠ 0); (2)顶点式:若二次函数图象的顶点坐标为( h , k ),则其解析式为 f ( x )= ①      a ( x - h ) 2 + k ( a ≠ 0)     ; (3)两根式:若相应一元二次方程的两根为 x 1 , x 2 ,则其解析式为 f ( x )= ②      a ( x - x 1 )( x - x 2 )( a ≠ 0)     . 2.二次函数的图象和性质 考点清单 解析式 f ( x )= ax 2 + bx + c ( a >0) f ( x )= ax 2 + bx + c ( a <0) 图象     定义域 R R 值域   ③             最值 f ( x ) min =   f ( x ) max =④             单调性 在⑤             上 单调递减, 在⑥             上 单调递增 在   上 单调递增, 在   上 单调递减 奇偶性 当 b =0时为偶函数,当 b ≠ 0时为非奇非偶函数 顶点 坐标   对称性 图象关于⑦ 　直线 x =-        对称 知识拓展     二次函数 f ( x )= ax 2 + bx + c ( a >0)在区间[ m , n ]上的最大值或最小值 如下: ①当-   ∈[ m , n ],即对称轴在所给区间内时, f ( x )的最小值在对称轴处取得, 其最小值是 f   =   ;若-   ≤   , 则 f ( x )的最大值为 f ( n );若-   ≥   ,则 f ( x )的最大值为 f ( m ). ②当-   ∉ [ m , n ],即给定的区间在对称轴的一侧时, f ( x )在[ m , n ]上是单调函 数,若-   < m ,则 f ( x )在[ m , n ]上是增函数, f ( x )的最小值是 f ( m ),最大值是 f ( n );若 n <-   ,则 f ( x )在[ m , n ]上是减函数, f ( x )的最小值是 f ( n ),最大值是 f ( m ). ③当不能确定-   是否属于区间[ m , n ]时,则需分类讨论,以对称轴与区间的 关系确定讨论的标准,然后转化为上述①②两种情形求最值. 考点二　幂函数 1.幂函数的定义 一般地,形如 y = x α ( α ∈R)的函数称为幂函数,其中 α 为常数. 2.幂函数 y = x , y = x 2 , y = x 3 , y =   , y =   的图象、 3.幂函数 y = x , y = x 2 , y = x 3 , y =   , y =   的性质 y = x y = x 2 y = x 3 y =   y = x -1 定义域 R R R [0,+ ∞ ) (- ∞ ,0) ∪ (0,+ ∞ ) 值域 R [0,+ ∞ ) R [0,+ ∞ ) (- ∞ ,0) ∪ (0,+ ∞ ) 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 (- ∞ ,0)上减, (0,+ ∞ )上增 增 增 (- ∞ ,0)上减, (0,+ ∞ )上减 定点 (0,0),(1,1) (1,1) 考法一 　求二次函数在闭区间上的最值(值域) 知能拓展 例1     (2018陕西渭南尚德中学一模,20)已知函数 f ( x )= x 2 +(2 a -1) x -3. (1)当 a =2, x ∈[-2,3]时,求函数 f ( x )的值域; (2)若函数 f ( x )在[1,3]上的最大值为1,求实数 a 的值. 解题导引     解析 　(1)当 a =2时, f ( x )= x 2 +3 x -3=   -   , 因为 x ∈[-2,3],所以 f ( x ) min = f   =-   , f ( x ) max = f (3)=15,所以所求函数的值域为   . (2) f ( x )图象的对称轴为直线 x =-   . ①当-   ≤ 1,即 a ≥ -   时, f ( x ) max = f (3)=6 a +3, 所以6 a +3=1,即 a =-   ,满足题意; ②当-   ≥ 3,即 a ≤ -   时, f ( x ) max = f (1)=2 a -3, 所以2 a -3=1,即 a =2,不满足题意; ③当1<-   <3,即-   < a <-   时, f ( x ) max 在端点处取得, 令 f (1)=1+2 a -1-3=1,得 a =2(舍去),令 f (3)=9+3(2 a -1)-3=1,得 a =-   (舍去).综上, 可知 a =-   . 方法总结 　二次函数求最值问题,一般先用配方法化成 y = a ( x - m ) 2 + n ( a ≠ 0) 的形式,得其图象的顶点坐标为( m , n ),对称轴方程为 x = m ,再结合二次函数的 图象求解,常见的有三种类型: (1)对称轴、区间都是给定的;(2)对称轴动,区间固定;(3)对称轴定,区间变 动.解决这类问题的思路是抓住“三点一轴”进行数形结合,三点指的是区 间两个端点及两个端点的中点,一轴指的是对称轴.具体方法是利用函数的 单调性及分类讨论的思想求解. 对于(2)、(3),通常要分对称轴在区间内、对称轴在区间外两大类情况进 行讨论. 简单地讲,轴在区间外,端点处取最值,轴在区间内,顶点和端点处有最值. 考法二 　一元二次方程根的分布 例2　 已知关于 x 的二次方程 x 2 +2 mx +2 m +1=0. (1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求 m 的取 值范围; (2)若方程两根均在区间(0,1)内,求 m 的取值范围. 解析 　令 f ( x )= x 2 +2 mx +2 m +1. (1)由条件知,抛物线 f ( x )= x 2 +2 mx +2 m +1与 x 轴的交点的横坐标分别在区间 (-1,0)和(1,2)内,如图所示, 则   ⇒   故 m 的取值范围是   . (2)抛物线与 x 轴的两个交点的横坐标均落在区间(0,1)内, 如图所示, 则   ⇒   故 m 的取值范围是   . 方法总结 　研究二次函数零点的分布,一般情况下需要从以下三个方面考虑: (1)一元二次方程根的判别式; (2)对应二次函数区间端点函数值的正负; (3)对应二次函数图象——抛物线的对称轴直线 x =-   与区间端点的位置关系. 设 x 1 , x 2 是实系数一元二次方程 ax 2 + bx + c =0( a >0)的两实根,则 x 1 , x 2 的分布范围 与一元二次方程系数之间的关系如下表: 零点的分布( m , n , p 为常数) 图象 满足条件 x 1 < x 2 < m     m < x 1 < x 2     x 1 < m < x 2   f ( m )<0 m < x 1 < x 2 < n     m < x 1 < n < x 2 < p     只有一个零点 在( m , n )之间     或 f ( m )· f ( n )<0 或   或 考法三 　幂函数的图象及性质的应用 例3 　(1)(2018贵州适应性考试,6)幂函数 y = f ( x )的图象经过点(3,   ),则 f ( x ) 是   (　　) A.偶函数,且在(0,+ ∞ )上是增函数 B.偶函数,且在(0,+ ∞ )上是减函数 C.奇函数,且在(0,+ ∞ )上是减函数 D.非奇非偶函数,且在(0,+ ∞ )上是增函数 (2)(2018北京东城月考,6)已知幂函数 f ( x )=( n 2 +2 n -2)·   ( n ∈Z)的图象关于 y 轴对称,且在(0,+ ∞ )上是减函数,则 n 的值为   (　　) A.-3　    B.1　    C.2　    D.1或2 解题导引　 (1)设 f ( x )= x a ,由 y = f ( x )的图象经过(3,   ),求出 f ( x )的解析式,然后 得出答案. (2)由幂函数的定义,得 n 2 +2 n -2=1,再由题意得 n 的值. 解析 　(1)设幂函数的解析式为 f ( x )= x a , 则 f (3)=3 a =   ,解得 a =   , 则 f ( x )=   =   ,是非奇非偶函数, 且在(0,+ ∞ )上是增函数.故选D. (2)由于 f ( x )为幂函数,所以 n 2 +2 n -2=1, 解得 n =1或 n =-3, 经检验,只有 n =1符合题意,故选B. 答案　 (1)D　(2)B