2020届高考理科数学全优二轮复习训练:小题专项训练1
小题专项训练
小题专项训练1 集合与简易逻辑
一、选择题
1.(2019年河南模拟)已知集合A={x|x2<4},B={x|x<2-x},则A∪B=( )
A.{x|-2
-1} D.{x|x>-2}
【答案】B
【解析】由x2<4得-2 B.∀x∉N*,x>
C.∃x0∉N*,x0> D.∃x0∈N*,x0>
【答案】D
【解析】命题p的否定是把“∀”改成“∃”,再把“x≤”改为“x0>”即可.
3.若集合A={2,3,4},B={x|x=n·m,m,n∈A,m≠n},则集合B中元素个数为( )
A.3 B.4
C.5 D.6
【答案】A
【解析】由题意,B中的元素有:2×3=6,2×4=8,3×4=12,所以B={6,8,12}.故选A.
4.(2019年浙江模拟)设a,b是两个平面向量,则“a=b”是“|a|=|b|”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】A
【解析】相等向量的模一定相等,模相等的向量不一定相等(因为方向可能不同),所以“a=b”是“|a|=|b|”的充分不必要条件.故选A.
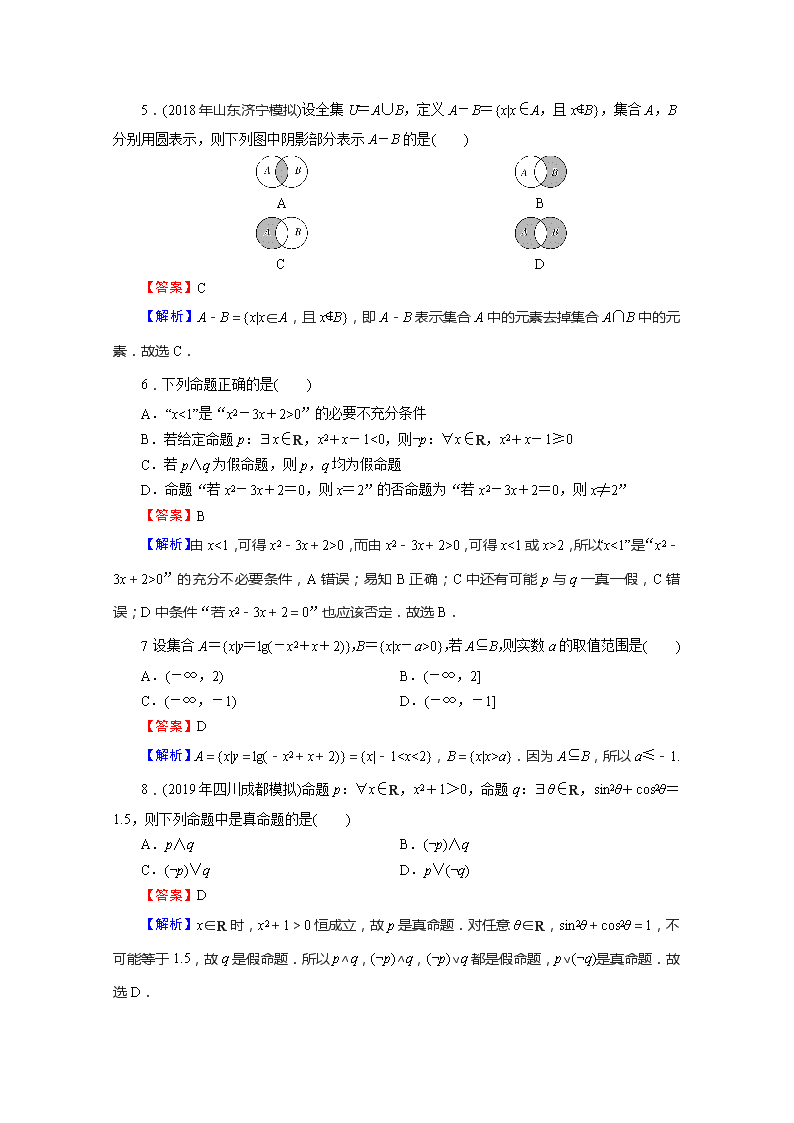
5.(2018年山东济宁模拟)设全集U=A∪B,定义A-B={x|x∈A,且x∉B},集合A,B分别用圆表示,则下列图中阴影部分表示A-B的是( )
A B
C D
【答案】C
【解析】A-B={x|x∈A,且x∉B},即A-B表示集合A中的元素去掉集合A∩B中的元素.故选C.
6.下列命题正确的是( )
A.“x<1”是“x2-3x+2>0”的必要不充分条件
B.若给定命题p:∃x∈R,x2+x-1<0,则¬p:∀x∈R,x2+x-1≥0
C.若p∧q为假命题,则p,q均为假命题
D.命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2=0,则x≠2”
【答案】B
【解析】由x<1,可得x2-3x+2>0,而由x2-3x+2>0,可得x<1或x>2,所以“x<1”是“x2-3x+2>0”的充分不必要条件,A错误;易知B正确;C中还有可能p与q一真一假,C错误;D中条件“若x2-3x+2=0”也应该否定.故选B.
7.设集合A={x|y=lg(-x2+x+2)},B={x|x-a>0},若A⊆B,则实数a的取值范围是( )
A.(-∞,2) B.(-∞,2]
C.(-∞,-1) D.(-∞,-1]
【答案】D
【解析】A={x|y=lg(-x2+x+2)}={x|-1a}.因为A⊆B,所以a≤-1.
8.(2019年四川成都模拟)命题p:∀x∈R,x2+1>0,命题q:∃θ∈R,sin2θ+cos2θ=1.5,则下列命题中是真命题的是( )
A.p∧q B.(¬p)∧q
C.(¬p)∨q D.p∨(¬q)
【答案】D
【解析】x∈R时,x2+1>0恒成立,故p是真命题.对任意θ∈R,sin2θ+cos2θ=1,不可能等于1.5,故q是假命题.所以p∧q,(¬p)∧q,(¬p)∨q都是假命题,p∨(¬q)是真命题.故选D.
9.(2019年浙江模拟)设a>0,b>0,则“lg(ab)>0”是“lg(a+b)>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】A
【解析】当lg(ab)>0时,ab>1,结合a>0,b>0可知a,b中至少有一个大于1,则a+
b>1,可以推出lg(a+b)>0.当lg(a+b)>0时,a+b>1,则ab>1不一定成立,如a=b=时,a+b>1但ab<1,所以推不出lg(ab)>0.综上所述,“lg(ab)>0”是“lg(a+b)>0”的充分不必要条件.
10.(2018年山东师大附中模拟)已知函数f(x)=x2-2x+3,g(x)=kx-1,则“|k|≤1”是“f(x)≥g(x)在R上恒成立”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】A
【解析】若f(x)≥g(x),则x2-(2+k)x+4≥0,所以f(x)≥g(x)在R上恒成立⇔(2+k)2-16≤0⇔-6≤k≤2;而|k|≤1⇔-1≤k≤1.所以“|k|≤1”是“f(x)≥g(x)在R上恒成立”的充分不必要条件.故选A.
11.设集合S={A0,A1,A2,A3},在S上定义运算⊕:Ai⊕Aj=Ak,k为i+j除以4的余数(i,j=0,1,2,3),则满足关系式(x⊕x)⊕A2=A0的x(x∈S)的个数为( )
A.4 B.3
C.2 D.1
【答案】C
【解析】因为x∈S={A0,A1,A2,A3},故x的取值有四种情况.若x=A0,根据定义得(x⊕x)⊕A2=A0⊕A2=A2,不符合题意,同理可以验证x=A1,x=A2,x=A3三种情况,其中x=A1,x=A3符合题意.故选C.
12.在下列结论中,正确的是( )
①命题p:“∃x0∈R,x-2≥0”的否定形式为¬p:“∀x∈R,x2-2<0”;
②O是△ABC所在平面上一点,若·=·=·,则O是△ABC的垂心;
③“M>N”是“M>N”的充分不必要条件;
④命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”.
A.①③ B.②④
C.①②③ D.①②④
【答案】D
【解析】由特称(存在性)命题与全称命题的关系可知①正确;∵·=·,∴·(-)=0,即·=0,∴⊥,同理可知⊥,⊥,故点O是△ABC的垂心,②正确;∵y=x是减函数,∴当M >N时,MN时,MN”是“M>N”的既不充分也不必要条件,③错误;由逆否命题的写法可知④
正确.综上,正确的结论是①②④.
二、填空题
13.已知A={y|y=10x-1},B={x|y=lg(4-x2)},则(∁RA)∩B=________.
【答案】(-2,-1]
【解析】∵A={y|y=10x-1}={y|y>-1},
∴∁RA={y|y≤-1}.又B={x|-2
查看更多