2018-2019学年福建省福州市三校联盟高一上学期期中联考数学试题

2018-2019学年福建省福州市三校联盟高一上学期期中联考数学试题

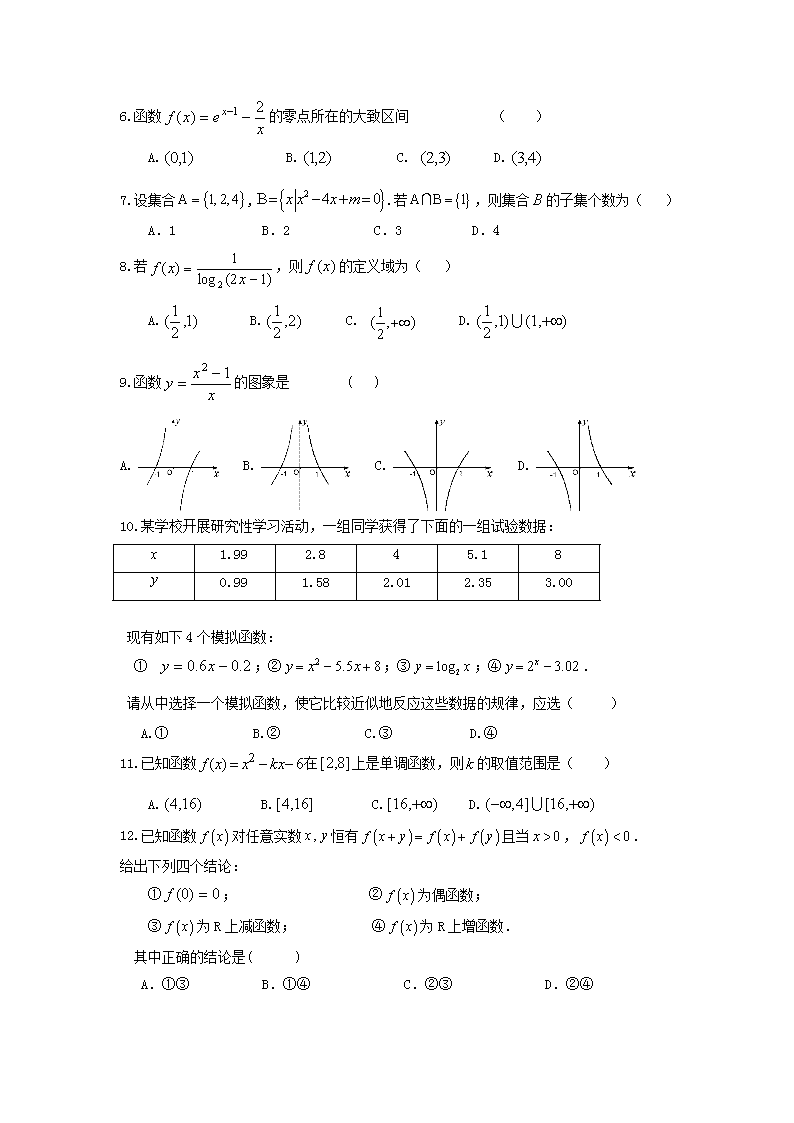
‎ ‎ ‎2018-2019学年福建省福州市三校联盟高一上学期期中联考数学试题 说明：1、本试卷分第I、II 两卷，考试时间：120分钟 满分：150分 ‎ ‎2、Ⅰ卷的答案用2B铅笔填涂到答题卡上；Ⅱ卷的答案用黑色签字笔填写在答题卡上。‎ 第Ⅰ卷（共60分） ‎ 一、 选择题：本大题共12个小题；每小题5分，共60分．在每小题给出的4个选项中，只有一项符合题目要求。‎ ‎1.集合A=，B=，则=（ ）‎ A. ｛1｝ B.｛3｝ C.｛1，3｝ D.｛2,3,4,5｝‎ ‎2.下列函数中哪个与函数相等（　　）‎ ‎ A． B． C． D．‎ ‎3.若偶函数在上是减函数，则（ ）‎ A. B. ‎ C. D. ‎ ‎4．三个数，，，它们之间的大小关系为（ ）‎ A.　 B.　 C. D.‎ ‎5．若，则等于（ ）‎ A. B. C. D.‎ ‎6.函数的零点所在的大致区间 （ ）‎ A. B. C. D.‎ ‎7.设集合,.若，则集合的子集个数为（ ）‎ A．1 B．2 C．3 D．4‎ ‎8.若，则的定义域为（ ）‎ A. B. C. D.‎ ‎9.函数的图象是 ( ) ‎ A. B. C. D.‎ ‎10.某学校开展研究性学习活动，一组同学获得了下面的一组试验数据：‎ ‎1.99‎ ‎2.8‎ ‎4‎ ‎5.1‎ ‎8‎ ‎0.99‎ ‎1.58‎ ‎2.01‎ ‎2.35‎ ‎3.00‎ 现有如下4个模拟函数：‎ ① ‎；②；③；④．‎ 请从中选择一个模拟函数，使它比较近似地反应这些数据的规律，应选（ ） ‎ A.① B.② C.③ D.④‎ ‎11.已知函数在上是单调函数，则的取值范围是（ ）‎ ‎ A. B. C. D.‎ ‎12.已知函数对任意实数恒有且当，．‎ 给出下列四个结论：‎ ‎①； ②为偶函数；‎ ‎③为R上减函数； ④为R上增函数．‎ 其中正确的结论是( 　　 )‎ A．①③ B．①④ C．②③ D．②④‎ 第Ⅱ卷（共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13.已知幂函数的图像经过点（2，）则 .‎ ‎14.已知集合，B，则= .‎ ‎15.已知函数，那么的值为 .‎ ‎16.若函数同时满足：①对于定义域上的任意，恒有 ‎ ‎②对于定义域上的任意，当时，恒有，则称函数为“理想函数”。给出下列四个函数中：‎ ‎① ； ② ； ③；④ ‎ 能被称为“理想函数”的有 （填相应的序号）．‎ 三、解答题：本大题共6小题,共70分,解答应写出文字说明，证明过程或演算步骤. ‎ ‎17.（本题满分10分）‎ ‎ (1)； (2)‎ ‎18.（本小题满分12分）‎ ‎ 已知集合，，.‎ （1） 求，； （2）若，求实数的取值范围.‎ ‎19.（本小题满分12分）‎ ‎2‎ ‎2‎ ‎4‎ ‎-2‎ ‎-2‎ 已知函数是定义在上的奇函数，且当时，．现已画出函数在轴左侧的图象，如图所示：‎ （1） 画出函数剩余部分的图象，并根据 图像写出函数的单调区间；（只写答案）‎ （1） 求函数的解析式.‎ 20. ‎（本小题满分12分）‎ 某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时，按销售利润的16 % 进行奖励;当销售利润超过10万元时，若超出万元，则超出部分按进行奖励。记奖金(单位:万元)，销售利润(单位:万元)‎ ‎(1)写出该公司激励销售人员的奖励方案的函数模型; ‎ ‎(2)如果业务员老张获得5.6万元的奖金，那么他的销售利润是多少万元。‎ 21. ‎（本小题满分12分)‎ 已知二次函数有两个零点1和-1.‎ ‎ （1）求的解析式；‎ ‎ （2）设，试判断函数在区间上的单调性并用定义证明；‎ ‎（3）由（2）函数在区间上，若实数t满足，求t的取值范围.‎ ‎22.（本小题满分12分）‎ 已知奇函数 (为常数）.‎ ‎（1）求的值； ‎ ‎（2）若函数有2个零点，求实数的取值范围；‎ ‎（3）若时，不等式恒成立，求实数的取值范围.‎ 福州三校联盟2018/2019学年第一学期中联考 高一数学参考答案 ‎ 一、填空题(每小题5分，共60分)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B C B C D B D D A C D A 二、选择题(每小题5分，共20分)‎ ‎13. 14. 15. 16.③④‎ 三、解答题：本大题共6小题,共70分,解答应写出文字说明，证明过程或演算步骤.‎ ‎17.（本题满分10分）‎ 解：(1)原式= ………………………5分 ‎(2)原式= ………………………10 分 ‎18.（本小题满分12分）‎ ‎ 解： （Ⅰ），………………………2 分 ‎∵ ………………………4 分 ‎ ……………6 分 ‎（Ⅱ）∵，‎ ‎①当时，满足，此时，得；……………8分 ‎②当时，要，则，………………………10 分 解得； ………………………11 分 由①②得， ∴的取值范围是 …………………12分 ‎19.（本小题满分12分）‎ 解：（1）画图…………………3分 函数的减区间为，增区间为.…………………6分 ‎（2）当时，函数是定义在上的奇函数， ………7分 当时， 则.‎ 函数是定义在上的奇函数，且当时，．‎ 当时， ………………10分 ‎ ……………………12分 ‎20.（本小题满分12分）‎ 解:(1)由题意得 ……………………6分 (2) 由，‎ 而y=5.6，所以……………………8分 因此解得 (万元)‎ 答:(1)略(2)老张的销售利润是34万元……………………12分 ‎21.（本小题满分12分） ‎ 解:(1)由题意得-1和1是函数的两根……………………1分 所以 ……………………2分 解得， 所以 ……………………3分 ‎ (2) 函数在区间上是减函数。…………………4 分 证明如下：设，则 ‎…………………6 分 ‎∵‎ ‎，，‎ ‎ ,即 函数在区间上是减函数。………………………8 分 ‎（3）‎ 又由（2）函数在区间上是递减函数。………………………9分 ‎，即 ………………………11分 解得 .∴实数的取值范围为.………………………12分 ‎22.解：（1）是定义在R上的奇函数， ……3分 ‎ （2）函数有2个零点方程有2个解 即有2个解 …………………5分 即函数图象有2个交点…………………6分 由图象得………………7分 ‎（3），即……………8分 即 , 在时恒成立 ………………9分 在R上单调递减， ………………10分 时， 的最大值为 ‎ ‎ …………12分