宁夏六盘山高级中学2020届高三下学期第3次周练卷数学（文）试题

宁夏六盘山高级中学2020届高三下学期第3次周练卷数学（文）试题

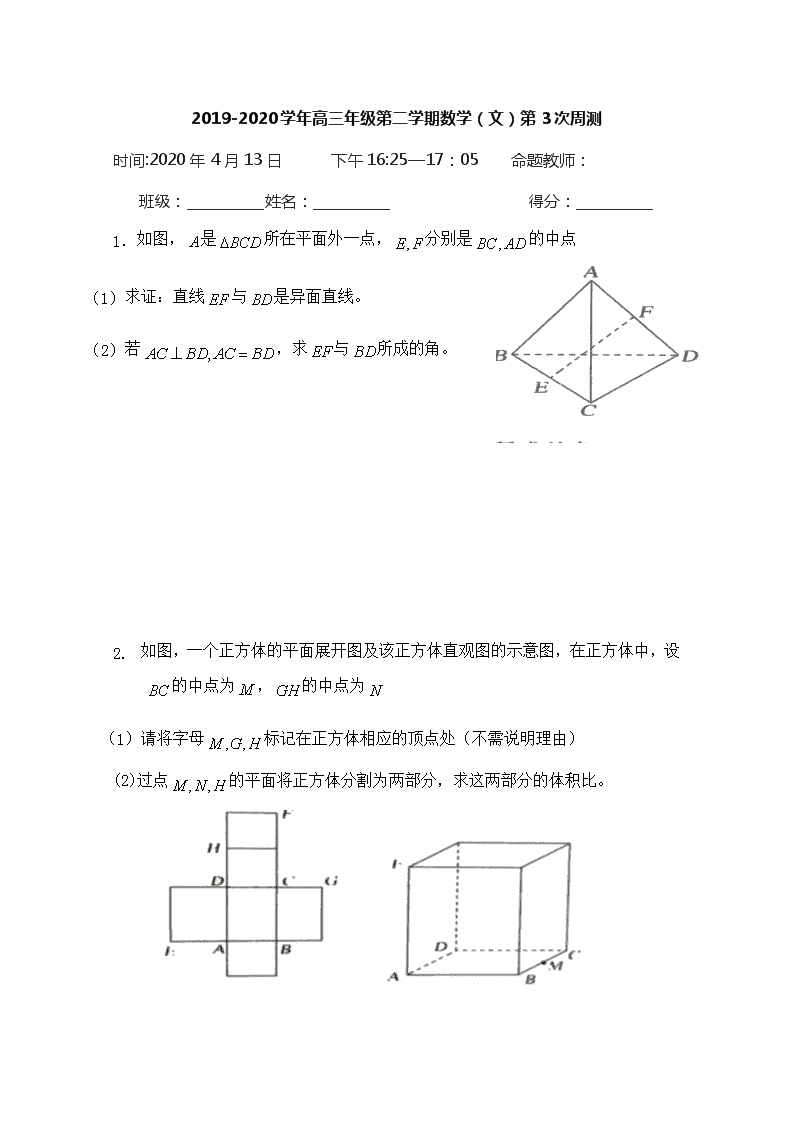
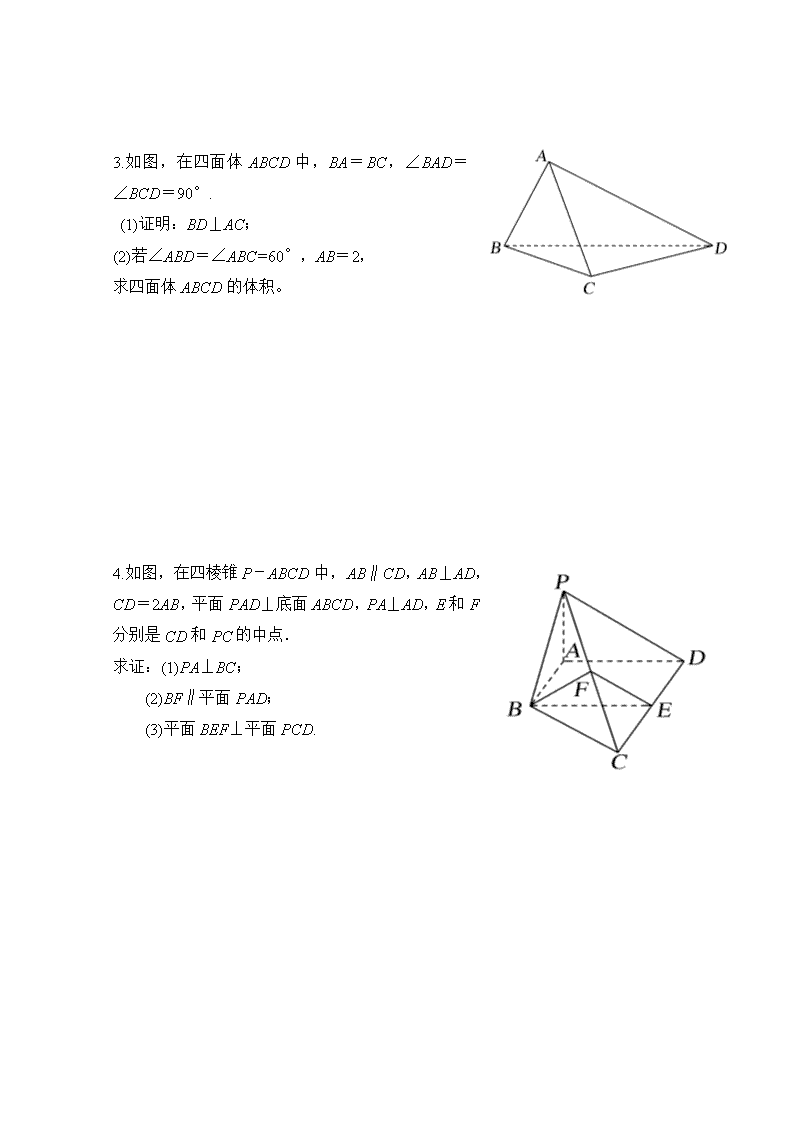
‎2019-2020学年高三年级第二学期数学（文）第3次周测 时间:2020年4月13日 下午16:25—17：05 命题教师：‎ 班级：___________姓名：___________ 得分：___________‎ 1． 如图，是所在平面外一点，分别是的中点 （1） 求证：直线与是异面直线。‎ （2） 若，求与所成的角。‎ 2. 如图，一个正方体的平面展开图及该正方体直观图的示意图，在正方体中，设的中点为，的中点为 ‎（1）请将字母标记在正方体相应的顶点处（不需说明理由）‎ ‎(2)过点的平面将正方体分割为两部分，求这两部分的体积比。‎ ‎3.如图，在四面体ABCD中，BA＝BC，∠BAD＝∠BCD＝90°.‎ ‎(1)证明：BD⊥AC；‎ ‎(2)若∠ABD＝∠ABC=60°，AB＝2，‎ 求四面体ABCD的体积。‎ ‎4.如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．‎ 求证：(1)PA⊥BC；‎ ‎(2)BF∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 参考答案 1. ‎（1）用反证法：假设直线与不是异面直线，则与共面，‎ 从而与共面，即与共面，这与是所在平面外一点矛盾，‎ 所以假设错误，直线与是异面直线。‎ ‎（2）取的中点，连接，‎ 因为分别是的中点 所以平行且等于，平行且等于 所以就是与所成的角或其补角。‎ 又因为 所以 所以 ‎2.解：（1）见图中 ‎（2）连接 过点的平面就是平面 它将正方体分割为两个同高的棱柱，高都是 底面分别是四边形和三角形，其面积比为3:1‎ 所以这两部分的体积比为3:1‎ ‎3．(1)证明　如图，作Rt△ABD斜边BD上的高AE，连CE.‎ ‎∵BA＝BC，BD＝BD，∠BAD＝∠BCD＝90°，‎ ‎∴Rt△ABD≌Rt△CBD.‎ 于是可得CE⊥BD.‎ 又AE∩CE＝E，‎ ‎∴BD⊥平面AEC，‎ ‎∵AC⊂平面AEC， ∴BD⊥AC.‎ ‎(2)在Rt△ABD中，BA＝2，∠ABD＝60°，‎ ‎∴BD＝4，AE＝，CE＝，‎ 又∵BA＝BC，∠ABC=60°，‎ ‎∴AC=BC=BA=2,‎ ‎∴可求得△AEC的面积S△AEC＝‎ 又BD⊥平面AEC，BD=4‎ ‎∴四面体ABCD的体积V＝·S△ACE·BD＝ ‎ ‎4.证明　(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，‎ 所以PA⊥底面ABCD.，‎ 因为BC⊂平面ABCD， 所以PA⊥BC；‎ ‎(2)取PD中点为G,连接FG,AG.‎ 因为F是PC的中点，E为CD的中点AB∥CD，CD＝2AB，，‎ 所以AB∥DE，且AB＝DE;FG//DE,FG=DE 所以四边形ABFG为平行四边形．‎ 所以BF∥AG，又因为BF⊄平面PAD，AG⊂平面PAD，‎ 所以BF∥平面PAD.‎ ‎(3)因为AB⊥AD，而且四边形ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 所以CD⊥平面PAD.‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF.所以CD⊥EF.‎ 又因为CD⊥BE，EF∩BE＝E，‎ 所以CD⊥平面BEF.‎ 所以平面BEF⊥平面PCD.‎