(全国I卷)2020届高三12月教育教学质量监测考试 数学(文)
2020届普通高中教育教学质量监测考试
全国Ⅰ卷 文科数学
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
3.全部答案写在答题卡上,写在本试卷上无效。
4.本试卷满分150分,测试时间120分钟。
5.考试范围:高考全部内容。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.
A. B. C. D.
2.已知集合M={x|8x2-9x+1≤0},N={x|y=},则
A. B. C. D.
3.已知双曲线C的两条渐近线的夹角为60°,则双曲线C的方程不可能为
A. B. C. D.
4.设向量m,n满足|m|=2,|n|=3,现有如下命题:
命题p:|m-2n|的值可能为9;
命题q:“(m-2n)⊥m”的充要条件为“cos
=”;
则下列命题中,真命题为
A.p B.p∧q C.(﹁p)∧q D.p∨(﹁q)
5.2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款、法国8款、荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国。A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香烃矿物油成分,则随机抽取3袋,
恰有2袋含有芳香烃矿物油成分的概率为
A. B. C. D.
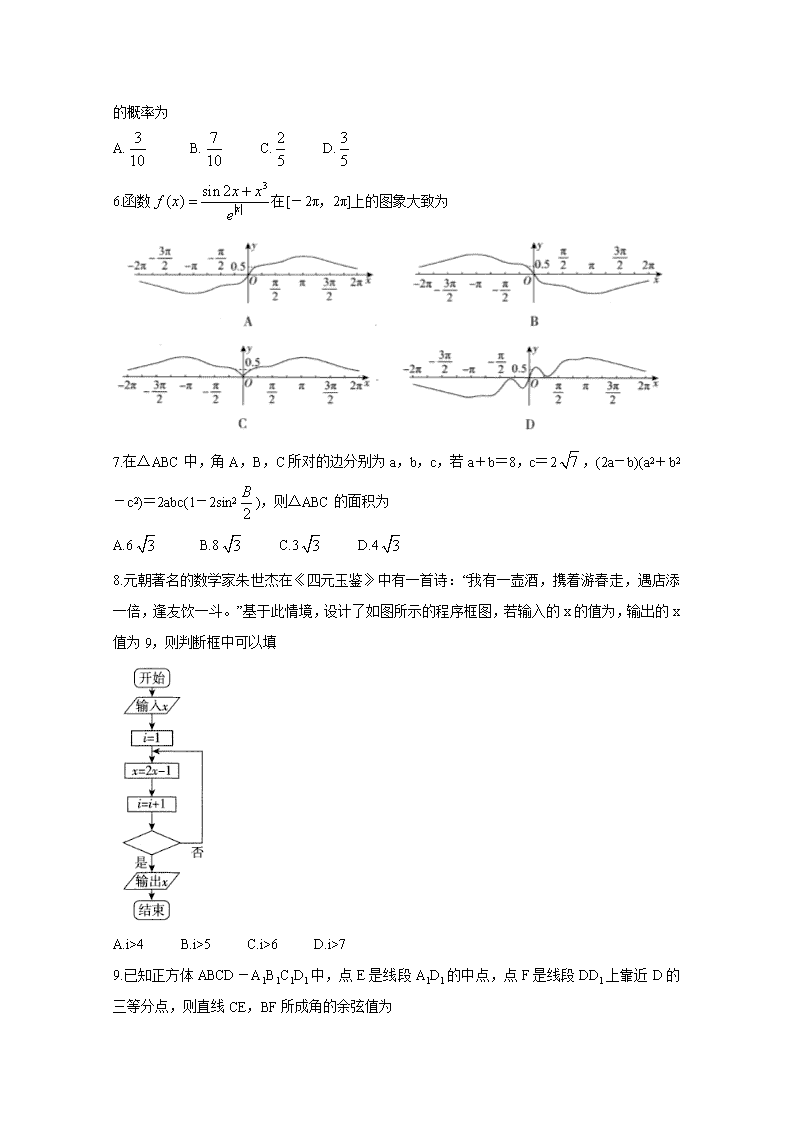
6.函数在[-2π,2π]上的图象大致为
7.在△ABC中,角A,B,C所对的边分别为a,b,c,若a+b=8,c=2,(2a-b)(a2+b2-c2)=2abc(1-2sin2),则△ABC的面积为
A.6 B.8 C.3 D.4
8.元朝著名的数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗。”基于此情境,设计了如图所示的程序框图,若输入的x的值为,输出的x值为9,则判断框中可以填
A.i>4 B.i>5 C.i>6 D.i>7
9.已知正方体ABCD-A1B1C1D1中,点E是线段A1D1的中点,点F是线段DD1上靠近D的三等分点,则直线CE,BF所成角的余弦值为
A. B. C. D.
10.已知函数,则函数f(x)的零点个数为
A.2 B.3 C.4 D.5
11.已知椭圆C:的左、右焦点分别为F1,F2第二象限的点M在椭圆C上,且|OM|=|OF2|,若椭圆C的离心率为,则直线MF2的斜率为
A.-4 B. C.-2 D.
12.已知函数f(x)=4|x+2|+cosπx,则f(4x-7)≤3的解集为
A. B. C. D.
第II卷
本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须作答。第22题~第23题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.已知函数f(x)=(4x2+mx)·ex,若曲线y=f(x)在(0,0)处的切线与直线y=4x相互垂直,则m=________。
14.已知实数x,y满足,则z=2x+y的最大值为_______。
15.若tan(α+β)=3,tanβ=,则________。
16.已知三棱锥P-ABC的外接球表面积为16π,∠PAB=∠PAC=∠ABC=2∠ACP=90°,则三棱锥P-ABC体积的最大值为________。
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)记等比数列的前n项和为Sn,且an=-2,S3=3。
(1)求数列{an}的通项公式;
(2)求数列{3n-2+an}的前n项和。
18.(本小题满分12分)某公司统计了2010~2018年期间公司年收入的增加值y(万元)以及相应的年增长率z,所得数据如下所示:
(1)通过散点图可知,可用线性回归模型拟合2010~2014年y与x的关系;
①求2010-2014年这5年期间公司年利润的增加值的平均数Y;
②求y关于x的线性回归方程;
(2)从哪年开始连续三年公司利润增加值的方差最大?(不需要说明理由。)
附:参考公式:回归直线方程中的斜率和截距的最小二乘估计公式分别为
。
19.(本小题满分12分)已知四棱锥S-ABCD中,∠SAD=∠ABC=∠BAD=90°,SA=AD=BC=AB=1,SC=2。
(1)求证:SA⊥BD;
(2)若P为线段SC的中点,求三棱锥A-SBP的体积。
20.(本小题满分12分)已知抛物线C:y2=2x,点M,N在抛物线C上。
(1)若直线MN的斜率为3,求线段MN中点的纵坐标;
(2)若P(-2,4),M,N三点共线,且|MN|2=|PM|·|PN|,求直线MN的方程。
21.(本小题满分12分)已知函数f(x)=lnx-4ax+2有两个零点x1,x2(x1≠x2)。
(1)求实数a的取值范围;
(2)求证:2ax1+2ax2>1。
请考生从第22、23题中任选一题作答,并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所选涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,
按本选考题的首题进行评分。
22.(本小题满分10分)[选修4-4:坐标系与参数方程]
在平面直角坐标系xOy中,直线l的参数方程为(t为参数)。以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4cosθ,且直线l与曲线C交于M,N两点。
(1)求直线l的普通方程以及曲线C的直角坐标方程;
(2)若A(0,1),求|AM|+|AN|的值。
23.(本小题满分10分)[选修4-5:不等式选讲]
已知函数f(x)=|x-m|+|2x+|(x>2)。
(1)若m=4,求不等式f(x)>5的解集;
(2)证明:。