2019届二轮复习规范答题技巧8

2019届二轮复习规范答题技巧8

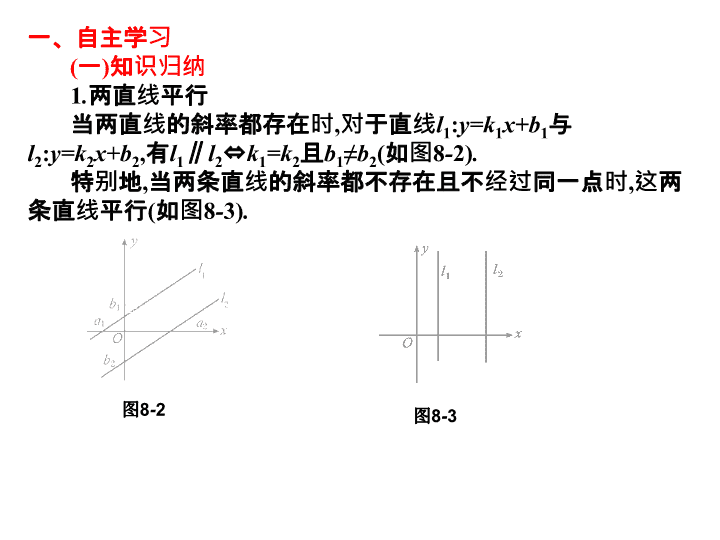
8.2 两条直线的位置关系 【考纲要求】　 1 . 理解两条直线平行与垂直的条件 , 能根据直线方程判定两条直线的位置关系 ; 2 . 会求两条直线的交点 , 了解点到直线的距离公式 . 【学习重点】　理解并能熟练运用两条直线平行与垂直的条件 . 一、自主学习 ( 一 ) 知识归纳 1 . 两直线平行 当两直线的斜率都存在时 , 对于直线 l 1 : y=k 1 x+b 1 与 l 2 : y=k 2 x+b 2 , 有 l 1 ∥ l 2 ⇔ k 1 =k 2 且 b 1 ≠ b 2 ( 如图 8 - 2) . 特别地 , 当两条直线的斜率都不存在 且不经过同一点 时 , 这两条直线平行 ( 如图 8 - 3) . 图 8 - 2 图 8 - 3 ( 二 ) 基础训练 2 3 x- 2 y- 4 = 0 4 . 求直线 l 1 :3 x+ 4 y+ 2 = 0 和 l 2 :2 x+y+ 3 = 0 的交点坐标 . 5 . 求点 P ( - 1,2) 到下列各直线的距离 d. (1)3 x- 4 y+ 5 = 0; (2)3 x= 5 . 二、探究提高 【例 1 】　 (1) 过点 P (2, - 1) 且平行于直线 x- 2 y+ 3 = 0 的直线方程为 ( 　　 ) A.2 x-y- 5 = 0 B.2 x+y- 3 = 0 C. x- 2 y- 4 = 0 D. x+ 2 y= 0 (2) 直线 ax+y+c= 0 与 x-ay+c= 0 的位置关系是 ( 　　 ) A. 平行 B. 垂直 C. 重合 D. 只有当 a ≠0 时才垂直 【例 2 】　求分别满足下列条件的直线方程 . (1) 经过点 A (1, - 3), 且平行于直线 4 x+ 7 y- 5 = 0 . (2) 经过点 C (1, - 3), 且垂直于直线 x+ 6 y- 8 = 0 . 分析 : 可以先根据直线的位置关系 , 求出直线的斜率 , 再求直线的方程 . 【例 3 】　求经过直线 l 1 : x+ 4 y- 8 = 0 与直线 l 2 :4 x-y- 15 = 0 的交点 , 且与直线 y= 3 x+ 4 平行的直线 l 的方程 . 分析 : 通过解方程组可以求出两条直线交点的坐标 , 再根据点斜式可以求出直线的方程 . 【例 4 】　 (1) 求平行直线 2 x- 3 y+ 8 = 0 与 2 x- 3 y- 5 = 0 间的距离 . (2) 已知点 A (1,3) 、 B (3,1) 、 C ( - 1,0), 求 △ ABC 的面积 . 分析 : 求两平行线之间的距离可以求一条直线上一点到另一条直线的距离 ; 求三角形的面积关键在于求它的高 , 它的高可以用点到直线的距离公式求顶点到对边的距离 . 三、达标训练 2 x-y- 7 = 0 x- 2 y- 2 = 0 3 x- 2 y+ 15 = 0 1 . 过点 A (5,3) 且与直线 4 x- 2 y+ 3 = 0 平行的直线方程是 　　　　　 .  2 . 过点 B (0, - 1) 且与直线 2 x+y- 4 = 0 垂直的直线方程是 　　　　　 .  3 . 已知点 A (2,4) 、 B ( - 4,8), 则线段 AB 的垂直平分线方程是 　　　　　 .  4 . 直线 2 x+ 4 y+ 6 = 0 与 x+ 2 y= 7 之间的距离是 　　　　　 .  5 . 求过直线 x= 2 与直线 3 x+ 2 y- 7 = 0 的交点 , 并与直线 x-y+ 1 = 0 垂直的直线 l 的方程 . 7 . 已知三条直线 2 x+ay+ 8 = 0,3 x+ 4 y= 10,2 y-x= 10 相交于一点 , 求 a.