高考文科数学复习备课课件：第三节　简单的逻辑联结词、全称量词与存在量词

高考文科数学复习备课课件：第三节　简单的逻辑联结词、全称量词与存在量词

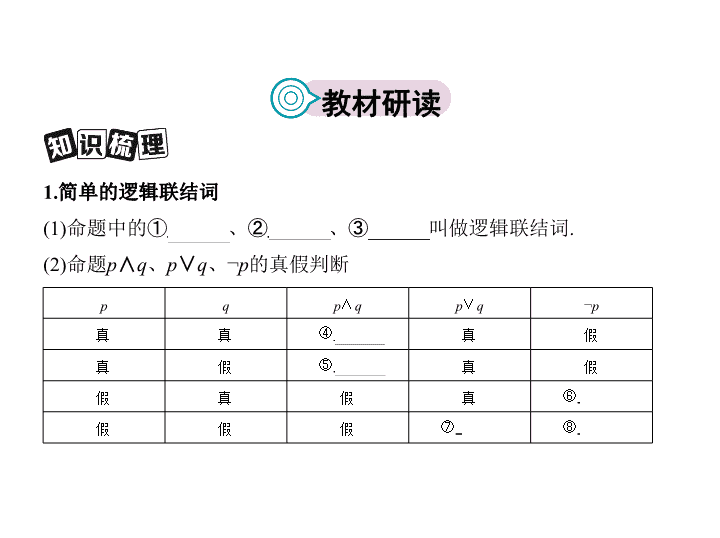
文数 课标版 第三节　简单的逻辑联结词、全称量词与存在量词 1.简单的逻辑联结词 (1)命题中的① 　且     、② 　或     、③ 　非     叫做逻辑联结词. (2)命题 p ∧ q 、 p ∨ q 、¬ p 的真假判断 教材研读 p q p ∧ q p ∨ q ¬ p 真 真 ④ 　真     真 假 真 假 ⑤ 　假     真 假 假 真 假 真 ⑥ 　真     假 假 假 ⑦ 　假     ⑧ 　真     2.全称量词与存在量词 (1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量 词,用“⑨      ∀      ”表示;含有全称量词的命题叫做全称命题. (2)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存 在量词,用“⑩      ∃      ”表示;含有存在量词的命题叫做特称命题. 3.含有一个量词的命题的否定 命题 命题的否定 ∀ x ∈ M , p ( x )        ∃ x 0 ∈ M ,¬ p ( x 0 )     ∃ x 0 ∈ M , p ( x 0 )        ∀ x ∈ M ,¬ p ( x )       　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)命题 p ∧ q 为假命题,则命题 p 、 q 都是假命题.   ( × ) (2)命题 p 和¬ p 不可能都是真命题.   (√) (3)若命题 p 、 q 至少有一个是真命题,则 p ∨ q 是真命题.   (√) (4)写特称命题的否定时,存在量词变为全称量词.   (√) (5) ∃ x 0 ∈ M , p ( x 0 )与 ∀ x ∈ M ,¬ p ( x )的真假性相反.   (√) 1.下列四个命题中的真命题为   (　　) A. ∃ x 0 ∈Z,1<4 x 0 <3　    B. ∃ x 0 ∈Z,5 x 0 +1=0 C. ∀ x ∈R, x 2 -1=0　    D. ∀ x ∈R, x 2 + x +2>0 答案     D　选项A中,   < x 0 <   ,与 x 0 ∈Z矛盾;选项B中, x 0 =-   ,与 x 0 ∈Z矛盾; 选项C中, x = ± 1,与 ∀ x ∈R矛盾;选项D中,由 Δ =1-8=-7<0可知D正确. 2.若命题 p : ∀ x ∈R,2 x 2 -1>0,则该命题的否定是   (　　) A. ∀ x ∈R,2 x 2 -1<0　    B. ∀ x ∈R,2 x 2 -1 ≤ 0 C. ∃ x ∈R,2 x 2 -1 ≤ 0　    D. ∃ x ∈R,2 x 2 -1>0 答案     C　全称命题的否定为特称命题.命题 p 的否定为 ∃ x ∈R,2 x 2 -1 ≤ 0,故选C. 3.已知命题 p : ∃ x 0 ∈R,   =1,则¬ p 是   (　　) A. ∀ x ∈R,2 x ≠ 1　    B. ∀ x ∉ R,2 x ≠ 1 C. ∃ x 0 ∈R,   ≠ 1　    D. ∃ x 0 ∉ R,   ≠ 1 答案     A　命题 p : ∃ x 0 ∈R,   =1的否定为¬ p : ∀ x ∈R,2 x ≠ 1,故选A. 4.命题 p :若sin x >sin y ,则 x > y ;命题 q : x 2 + y 2 ≥ 2 xy ,下列命题为假命题的是   (　　) A. p 或 q 　    B. p 且 q 　    C. q 　    D.¬ p 答案     B　取 x =   , y =   ,可知命题 p 是假命题;由( x - y ) 2 ≥ 0恒成立,可知命 题 q 是真命题,故¬ p 为真命题, p 或 q 是真命题, p 且 q 是假命题,故选B. 5.已知命题 p :若 x > y ,则- x <- y ,命题 q :若 x > y ,则 x 2 > y 2 .在命题① p ∧ q ;② p ∨ q ; ③ p ∧(¬ q );④(¬ p )∨ q 中,真命题是   (　　) A.①③　    B.①④　    C.②③　    D.②④ 答案     C　依题意可知,命题 p 为真命题,命题 q 为假命题,则¬ p 为假命题, ¬ q 为真命题. 由真值表可知 p ∧ q 为假命题, p ∨ q 为真命题, p ∧(¬ q )为真命题,(¬ p )∨ q 为 假命题. 考点一　全称命题与特称命题的真假判断 典例1 　(1)下列命题中的假命题是   (　　) A. ∀ x ∈ R ,2 x -1 >0　    B. ∀ x ∈ N * ,( x -1) 2 >0 C. ∃ x ∈ R ,lg x <1　    D. ∃ x ∈ R ,tan x =2 (2)下列命题中,真命题是   (　　) A. ∀ x ∈ R , x 2 - x -1>0 B. ∀ α , β ∈ R ,sin( α + β )0; ② ∀ x ∈ N , x 4 ≥ 1; ③ ∃ x ∈ Z , x 3 <1; ④ ∃ x ∈ Q , x 2 =3; ⑤ ∀ x ∈ R , x 2 -3 x +2=0; ⑥ ∃ x ∈ R , x 2 +1=0. 其中是真命题的序号为 　　　     . 答案 　①③ 解析 　①由于 ∀ x ∈ R ,都有 x 2 ≥ 0, 因而有 x 2 +2 ≥ 2,即 x 2 +2>0, 所以命题“ ∀ x ∈ R , x 2 +2>0”是真命题. ②由于0∈ N ,当 x =0时, x 4 ≥ 1不成立,所以命题“ ∀ x ∈ N , x 4 ≥ 1”是假命 题. ③由于-1∈ Z ,当 x =-1时, x 3 <1,所以命题“ ∃ x ∈Z, x 3 <1”是真命题. ④由于使 x 2 =3成立的数只有 ±   ,而它们都不是有理数,因此,没有任何 一个有理数的平方能等于3,所以命题“ ∃ x ∈ Q , x 2 =3”是假命题. ⑤由于只有当 x =2或 x =1时,满足 x 2 -3 x +2=0,所以命题“ ∀ x ∈ R , x 2 -3 x +2= 0”是假命题. ⑥由于不存在一个实数 x 使 x 2 +1=0成立,所以命题“ ∃ x ∈ R ,x 2 +1=0”是 假命题. 考点二　含有一个量词的命题的否定 典例2 　(1)(2015课标Ⅰ,3,5分)设命题 p : ∃ n ∈ N , n 2 >2 n ,则¬ p 为   (　　) A. ∀ n ∈ N , n 2 >2 n 　    B. ∃ n ∈ N , n 2 ≤ 2 n C. ∀ n ∈ N , n 2 ≤ 2 n 　    D. ∃ n ∈ N , n 2 =2 n (2)命题“对任意 x ∈ R ,都有 x 2 ≥ ln 2”的否定为   (　　) A.对任意 x ∈ R ,都有 x 2 x B. ∃ x ∈   ,cos x < x C. ∀ x ∈   ,cos x > x D. ∀ x ∈   ,cos x ≤ x 答案     C　原命题是一个特称命题,其否定是一个全称命题,而“cos x ≤ x ”的否定是“cos x > x ”.故选C. 2-2    (2017福建南平模拟)设命题 p : ∀ x ∈R, x 2 +1>0,则¬ p 为   (　　) A. ∃ x 0 ∈ R ,   +1 ≤ 0　     B. ∃ x 0 ∈ R ,   +1>0 C. ∀ x ∈ R , x 2 +1<0　     D. ∀ x ∈ R , x 2 +1 ≤ 0 答案    A　根据全称命题的否定是特称命题得到命题 p 的否定¬ p : ∃ x 0 ∈ R ,   +1 ≤ 0,故选A. 考点三　含逻辑联结词的命题的真假判断 典例3　 (1)若命题 p :函数 y = x 2 -2 x 的单调递增区间是[1,+ ∞ ),命题 q :函数 y = x -   的单调递增区间是[1,+ ∞ ),则   (　　) A. p ∧ q 是真命题　    B. p ∨ q 是假命题 C.¬ p 是真命题　    D.¬ q 是真命题 (2)已知命题 p 1 :函数 y =2 x -2 - x 在R上为增函数, p 2 :函数 y =2 x +2 - x 在R上为减函 数,则在命题 q 1 : p 1 ∨ p 2 , q 2 : p 1 ∧ p 2 , q 3 :(¬ p 1 )∨ p 2 , q 4 : p 1 ∧(¬ p 2 )中,真命题是   (    ) A. q 1 , q 3 　    B. q 2 , q 3 　     C. q 1 , q 4 　    D. q 2 , q 4 解析 　(1)易知 p 是真命题;因为函数 y = x -   的单调递增区间是(- ∞ ,0)和 (0,+ ∞ ),所以 q 是假命题,所以 p ∧ q 为假命题, p ∨ q 为真命题,¬ p 为假命题, ¬ q 为真命题. (2)∵ y =2 - x =   在R上为减函数, ∴ y =-2 - x =-   在R上为增函数, 又∵ y =2 x 在R上为增函数, ∴ y =2 x -2 - x 在R上为增函数,故 p 1 是真命题. 易知 y =2 x +2 - x 在R上为减函数是错误的,故 p 2 是假命题. ∴ q 1 : p 1 ∨ p 2 是真命题, q 2 : p 1 ∧ p 1 是假命题, q 3 :(¬ p 1 )∨ p 2 是假命题, q 4 : p 1 ∧ (¬ p 2 )是真命题,故选C. 答案 　(1)D　(2)C 方法技巧 (1)含逻辑联结词的命题真假判断的步骤: ①确定复合命题的结构形式; ②判断其中简单命题的真假; ③根据真值表判断复合命题的真假. (2)含逻辑联结词的命题真假判断以真值表为标准.可简记为: p ∧ q ,同真 则为真,其余为假; p ∨ q ,有真则为真,其余为假;¬ p 与 p 的真假相反. 3-1 　设 a , b , c 是非零向量.已知命题 p :若 a · b =0, b · c =0,则 a · c =0;命题 q :若 a ∥ b , b ∥ c ,则 a ∥ c .则下列命题中是真命题的是   (　　) A. p ∨ q 　     B. p ∧ q C.(¬ p )∧(¬ q )　    D. p ∨(¬ q ) 答案     A　由题意知命题 p 为假命题,命题 q 为真命题,所以 p ∨ q 为真命 题.故选A. 3-2　已知命题 p , q ,“¬ p 为真”是“ p ∧ q 为假”的   (　　) A.充分不必要条件　     B.必要不充分条件 C.充要条件　     D.既不充分也不必要条件 答案     A　因为¬ p 为真,所以 p 为假,那么 p ∧ q 为假,所以“¬ p 为真”是 “ p ∧ q 为假”的充分条件; 反过来,若“ p ∧ q 为假”,则“ p 真 q 假”或“ p 假 q 真”或“ p 假 q 假”,所 以由“ p ∧ q 为假”不能推出“¬ p 为真”. 综上可知,“¬ p 为真”是“ p ∧ q 为假”的充分不必要条件. 考点四　利用复合命题的真假求参数范围 典例4 　已知命题 p :关于 x 的不等式 a x >1( a >0,且 a ≠ 1)的解集是{ x | x <0}, 命题 q :函数 y =lg( ax 2 - x + a )的定义域为 R ,如果 p ∨ q 为真命题, p ∧ q 为假命 题,则实数 a 的取值范围为 　　　　　　　     . 答案        ∪ [1,+ ∞ ) 解析 　由关于 x 的不等式 a x >1( a >0,且 a ≠ 1)的解集是{ x | x <0},知0< a <1; 由函数 y =lg( ax 2 - x + a )的定义域为 R , 知不等式 ax 2 - x + a >0的解集为 R , 则   解得 a >   . 因为 p ∨ q 为真命题, p ∧ q 为假命题, 所以 p 和 q 一真一假, 即“ p 假 q 真”或“ p 真 q 假”, 故   或   解得 a ≥ 1或0< a ≤   , 故实数 a 的取值范围是   ∪ [1,+ ∞ ). 方法技巧 根据复合命题的真假求参数范围的步骤: (1)先求出每个简单命题是真命题时参数的取值范围; (2)再根据复合命题的真假确定各个简单命题的真假情况(有时不一定 只有一种情况); (3)最后由(2)的结果求出满足条件的参数的取值范围. 变式4-1 　在本例命题 p , q 不变的条件下,若 p ∧ q 为真,求实数 a 的取值范 围. 解析 　由 p ∧ q 为真知 p , q 都为真. ∴ a 的取值范围为   . 变式4-2 　在本例命题 p , q 不变的条件下,若命题 q ∨( p ∧ q )为真、¬ p 为 真,求实数 a 的取值范围. 解析 　由命题 q ∨( p ∧ q )为真、¬ p 为真知 p 假、 q 真, 由 p 假得 a ≤ 0或 a ≥ 1; 由 q 真得 a >   . ∴实数 a 的取值范围为[1,+ ∞ ).