微专题---函数对称中心的应用

微专题---函数对称中心的应用

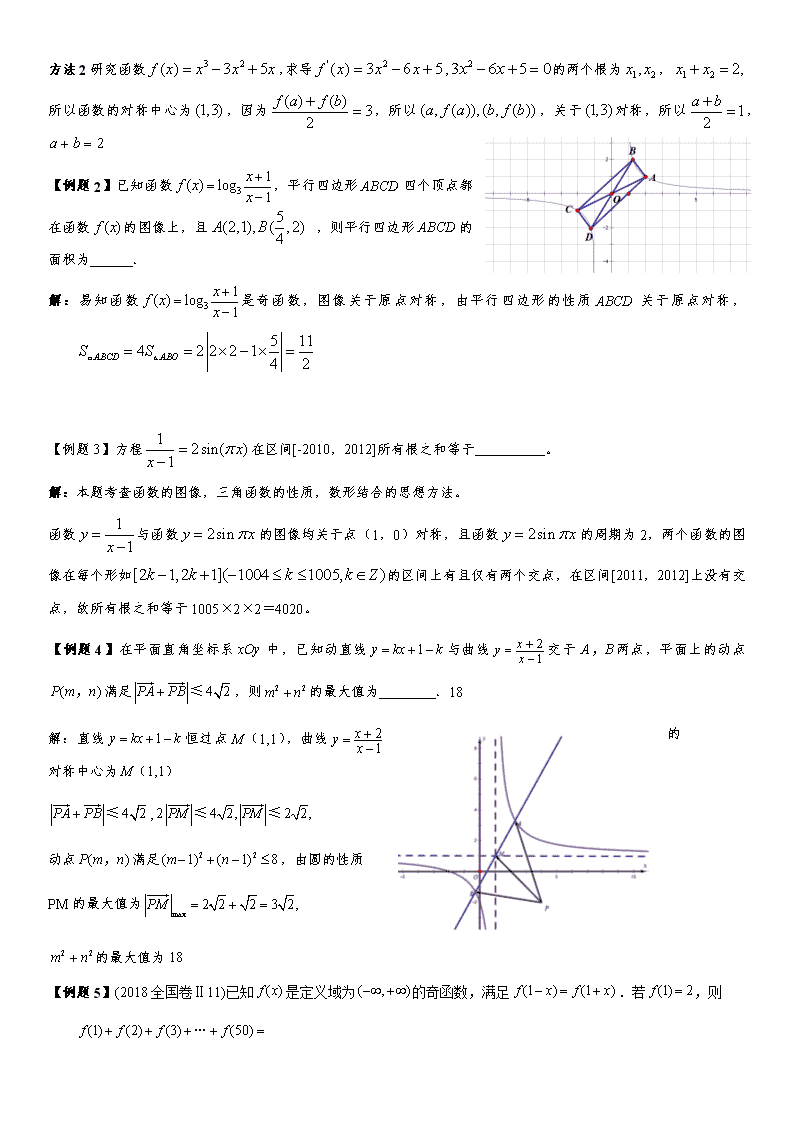
微专题---函数的对称中心的应用 ‎【知识导引】‎ ‎1.三次函数是中心对称曲线，函数图象关于点成中心对称 证明：三次函数关于点（m，n）对称的充要条件是，即+，‎ 整理得，‎ 据多项式恒等对应系数相等,可得 且=，‎ 从而三次函数是中心对称曲线，且对称中心是； ‎ 实际上：其导函数为f′(x)=3ax2+2bx＋c，对称轴为x=－，所以对称中心的横坐标也就是导函数的对称轴，可见，y＝f(x)图象的对称中心在导函数y＝f′(x)的对称轴上，且又是两个极值点的中点，同时也是二阶导为零的点。‎ ‎2.①函数是中心对称曲线，函数图象关于点成中心对称 ‎②函数是奇函数，函数图象关于点成中心对称 ‎3. ，满足，恒有，那么函数的图象有对称中心;反过来，如果函数的图象有对称中心，，满足，恒有.‎ ‎【例题1】已知实数分别满足，， 则的值为 ．‎ 解：方法1，，变形为 变形为考察函数，它为奇函数，且在定义域是增函数，，所以，。‎ 方法2研究函数，求导,的两个根为，所以函数的对称中心为，因为，所以，关于对称，所以，‎ ‎【例题2】已知函数，平行四边形ABCD四个顶点都在函数的图像上，且 ，则平行四边形ABCD的面积为 ．‎ 解：易知函数是奇函数，图像关于原点对称，由平行四边形的性质ABCD关于原点对称，‎ ‎【例题3】方程在区间[-2010，2012]所有根之和等于 。‎ 解：本题考查函数的图像，三角函数的性质，数形结合的思想方法。‎ 函数与函数的图像均关于点（1，0）对称，且函数的周期为2，两个函数的图像在每个形如的区间上有且仅有两个交点，在区间[2011，2012]上没有交点，故所有根之和等于1005×2×2＝4020。‎ ‎【例题4】在平面直角坐标系xOy中，已知动直线与曲线交于两点，平面上的动点满足，则的最大值为 ．18‎ 解：直线恒过点M（1,1），曲线的 对称中心为M（1,1）‎ ‎,‎ 动点满足，由圆的性质 PM的最大值为 的最大值为18‎ ‎【例题5】(2018全国卷Ⅱ11)已知是定义域为的奇函数，满足．若，则 A． B．0 C．2 D．50‎ 解：因为是定义域为的奇函数，且，‎ 所以,‎ 因此，‎ 因为，所以，‎ ‎，从而，选C.‎ ‎【例题6】（2020•全国2卷）设函数，则f(x)（ ）‎ A. 是偶函数，且在单调递增 B. 是奇函数，且在单调递减 C. 是偶函数，且在单调递增 D. 是奇函数，且在单调递减 解:由得定义域为，关于坐标原点对称，‎ 又，‎ 为定义域上的奇函数，可排除AC；当时，，‎ 在上单调递增，在上单调递减，‎ 在上单调递增，排除B；‎ 当时，，‎ 在上单调递减，在定义域内单调递增，‎ 根据复合函数单调性可知：在上单调递减，D正确，故选：D.‎ ‎【例题7】已知函数,则 的值为 ． ‎ 解:由,，关于点(1,0)对称，‎ 所以，关于点(1,0)对称 关于点(1,-2)对称 ‎，‎ ‎ .‎ ‎【例题8】（2020道里区校级模拟）已知等差数列公差为2020，函数，且，记为前n和，则为 ． ‎ A. B. C. D. ‎ 解:由,，关于点(,0)对称，‎ 所以，关于点对称 关于点对称，且在上单调递增，，‎ ‎ ,结合等数列的性质和对称中心的概念，所以故答案为A.‎ ‎【评注】等差数列的公差2020没有用到，主要使用了等差数列的性质：到首末等距离的两项的和相等,即 ‎【变式练习】‎ ‎1. 已知函数,实数a,b满足则 ‎2.已知直线l与曲线相交，交点依次为A,B,C不同的交点则直线l的方程为 ．‎ ‎3.设直线l与曲线有三个不同的交点A,B,C，且则直线l的方程为 ．‎ ‎4. 已知直线l与曲线有三个不同的交点，且则.‎ ‎5.已知直线l与曲线相交，交点依次为A,B,C不同的交点则直线l的方程为 ． ‎ ‎6.已知函数,实数m,n满足则 ‎7.已知直线l与曲线相交，交点依次为A,B,C不同的交点则直线l的方程为 ． ‎ ‎8.若函数有3个不同的零点，则实数a的取值范围为 ． ‎ ‎9.（2016全国卷Ⅱ理科12）已知函数满足，若函数与图像的交点为则（ ）‎ ‎（A）0 （B） （C） （D）‎ ‎10.已知等差数列满足，则其2018的和为 ． ‎ ‎11.已知函数的最大值为M,最小值为m,，则为 ． ‎ ‎【变式练习答案】‎ ‎1.4,2.,3. ，4. 7,5. y=2x-3,6.6,7. y=3x+1,8. ，9.【答案】B ‎【解析】由得关于对称，而也关于对称，‎ ‎∴对于每一组对称点 ，∴，故选B．考点： 函数图象的性质 ‎10.0,11.2.‎