高中数学第8章圆锥曲线方程（第14课时）抛物线及其标准方程(2)

高中数学第8章圆锥曲线方程（第14课时）抛物线及其标准方程(2)

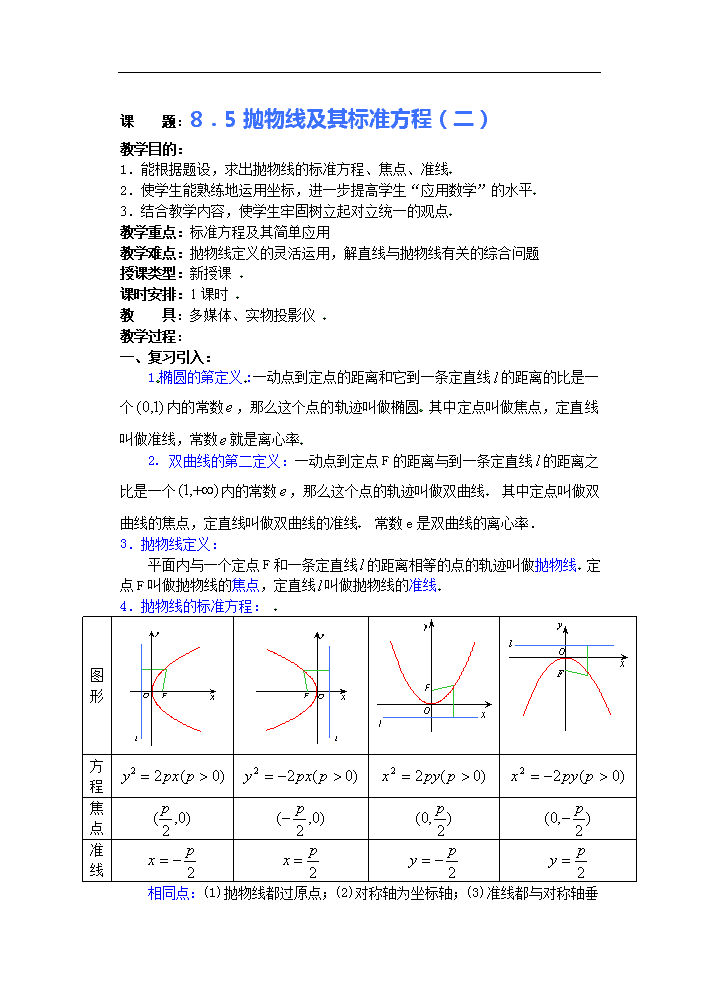
课 题：8．5抛物线及其标准方程（二）‎ 教学目的： ‎ ‎1．能根据题设，求出抛物线的标准方程、焦点、准线 ‎ ‎2．使学生能熟练地运用坐标，进一步提高学生“应用数学”的水平 ‎ ‎3．结合教学内容，使学生牢固树立起对立统一的观点 ‎ 教学重点：标准方程及其简单应用 教学难点：抛物线定义的灵活运用，解直线与抛物线有关的综合问题 ‎ 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、复习引入： ‎ ‎1 椭圆的第定义:一动点到定点的距离和它到一条定直线的距离的比是一个内的常数，那么这个点的轨迹叫做椭圆 其中定点叫做焦点，定直线叫做准线，常数就是离心率 ‎2. 双曲线的第二定义：一动点到定点F的距离与到一条定直线的距离之比是一个内的常数，那么这个点的轨迹叫做双曲线 其中定点叫做双曲线的焦点，定直线叫做双曲线的准线 常数e是双曲线的离心率．‎ ‎3．抛物线定义：‎ 平面内与一个定点F和一条定直线的距离相等的点的轨迹叫做抛物线 定点F叫做抛物线的焦点，定直线叫做抛物线的准线 ‎ ‎4．抛物线的标准方程： ‎ 图形 方程 焦点 准线 相同点：‎ ‎(1)抛物线都过原点；(2)对称轴为坐标轴；(3)准线都与对称轴垂直，垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的，即 ‎ 不同点：(1)图形关于X轴对称时，X为一次项，Y为二次项，方程右端为、左端为；图形关于Y轴对称时，X为二次项，Y为一次项，方程右端为，左端为 （2）开口方向在X轴（或Y轴）正向时，焦点在X轴（或Y轴）的正半轴上，方程右端取正号；开口在X轴（或Y轴）负向时，焦点在X轴（或Y轴）负半轴时，方程右端取负号 ‎ 二、讲解范例：‎ 例1 点M与点F（4,0）的距离比它到直线的距离小1，求点M的轨迹方程 ‎ 解析：可知原条件M点到F（4，0）和到x＝－4距离相等，由抛物线的定义，点M的轨迹是以F（4，0）为焦点，x＝－4为准线的抛物线．∴‎ 所求方程是 例2 斜率为1的直线经过抛物线的焦点，与抛物线相交于两点A、B，求线段AB的长 分析：思路一：解方程组，得交点的坐标，利用两点间距离公式解之 思路二：同思路一相同，但不解方程组，利用根与系数的关系，解之 思路三：利用根与系数关系及抛物线的定义来解之 思路四：利用弦长公式解之（以后给出）‎ 解析：如图，由抛物线的标准方程可知，抛物线焦点的坐标为F(1，0)， 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　所以直线AB的方程为 即 ①‎ 将方程①代入抛物线方程，得 ‎ 化简得 解这个方程，得 ，‎ 将，代入方程①中，得 ‎，‎ 即A,B的坐标分别是（，），（，）‎ ‎∴‎ 另法：在图中，由抛物线的定义可知，|AF|等于点A到准线x=－1的距离|AD|，而|AD|=＋1．同理|BF|＝|BC|=＋1，于是得 ‎|AB|=|AF＋|BF|=＋＋2．‎ 由此可以看到，本题在得到方程后，‎ 根据根与系数的关系可以直接得到 ＋＝6．‎ 于是立即可以求出|AB|=6＋2=8．‎ 例3 已知抛物线的顶点在原点，对称轴为x轴，抛物线上的点M（-3，m）到焦点的距离等于5，求抛物线的方程和m的值 解析：由 M（-3，m）到焦点的距离等于5‎ ‎ M（-3，m）到准线的距离等于5‎ 所求抛物线的方程为 三、课堂练习：‎ ‎1．抛物线y2=ax(a≠0)的准线方程是 ( )‎ ‎(A)x= - (B)x= (C)x= - (D)x=‎ 翰林汇2．已知M(m,4)是抛物线x2=ay上的点，F是抛物线的焦点，若|MF|=5，则此抛物线的焦点坐标是 ( )‎ ‎(A)(0,-1) (B)(0,1) (C)(0,-2) (D)(0,2)翰林汇 ‎3．抛物线的顶点在原点，对称轴为x轴，焦点在直线3x-4y-12=0上，此抛物线的方程是 ( )‎ ‎(A)y2=16x (B)y2=12x (C)y2= -16x (D)y2= -12x翰林汇 ‎4．抛物线2y2＋x＋=0的焦点坐标是 ( )‎ ‎ (A)(-，0) (B)(0，-) (C)(-，0) (D)(0，-)‎ 翰5．过点(0，1)且与抛物线y2=x只有一个公共点的直线有 ( )‎ ‎(A)一条 (B)两条 (C)三条 (D)无数条 翰林6．若直线3x＋4y＋24=0和点F（1，－1）分别是抛物线的准线和焦点，则此抛物线的顶点坐标是 ( )‎ ‎(A)(1,2) (B)(4,3) (C) (D)(－2,－5)翰林汇 ‎7．过抛物线y2=4x的焦点F作倾斜角为的直线交抛物线于A、B两点，则AB的长是 ( )‎ ‎ (A) (B)4 (C)8 (D)2‎ 练习的答案：1 A 翰林汇2 B 翰林汇3 A 翰林汇4 C 翰林汇5 C 翰林汇6 C 7 C ‎ 四、小结 ：本课主要讲解了四道例题，从不同的角度对如何灵活运用抛物线的定义、标准方程、焦点、准线等知识解决有关问题进行了巩固训练。 ‎ 五、课后作业：‎ ‎1．选择题 ‎（1）已知抛物线方程为y＝ax2（a＞0），则其准线方程为（　　　）‎ ‎(A) (B) (C) (D) ‎ ‎（2）抛物线（m≠0）的焦点坐标是（　　　）(A) （0，）或（0，）(B) （0，）(C) （0，）或（0，）(D) （0，）‎ ‎（3）焦点在直线3x－4y－12＝0上的抛物线标准方程是（　　　）‎ ‎(A) y2＝16x或x2＝16y (B) y2＝16x或x2＝12y ‎(C) x2＝－12y或y2＝16x (D) x2＝16y或y2＝－12x ‎2．根据下列条件写出抛物线的标准方程（　　　）‎ ‎（1）过点（－3，4）‎ ‎（2）过焦点且与x轴垂直的弦长是16‎ ‎3．点M到点（0，8）的距离比它到直线y＝－7的距离大1，求M点的轨迹方程．‎ ‎4．抛物线y2＝16x上的一P到x轴的距离为12，焦点为F，求｜PF｜的值．‎ 答案：‎ ‎1．（1）D （2）B （3）C ‎ ‎2．（1）或 （2）y2＝±16x ‎3．x2＝32y 4．13 六、板书设计（略）‎ 七、测试题（时间10分钟，满分10分）‎ ‎（一）．选择题（每小题2分，共4分）‎ ‎1．抛物线y＝2x2的焦点坐标是（　　　）‎ ‎(A) （0，） (B) （0，） (C) （，0） (D) （，0）‎ ‎2．以椭圆的中心为顶点，左准线为准线的抛物线标准方程（　　）(A) y2＝25x (B) (C) (D) ‎ ‎（二）．填空题（每小题2分，共4分）‎ ‎3．顶点在原点，焦点在y轴上，且过点P（4，2）的抛物线方程是　　　　　　　‎ ‎4．平面上的动点P到点A（0，－2）的距离比到直线l：y＝4的距离小2，则动点P的轨迹方程是　　　　　　　‎ ‎（三）．解答题（2分）‎ ‎5．已知抛物线y2＝x上的点M到准线的距离等于它到顶点的距离，求P点的坐标．‎ 测试题答案：1．B 2．A 3．x2＝8y 4．x2＝－8y 5．（，）‎ 八、课后记： ‎