2019届二轮复习三角恒等式教案（全国通用）

2019届二轮复习三角恒等式教案（全国通用）

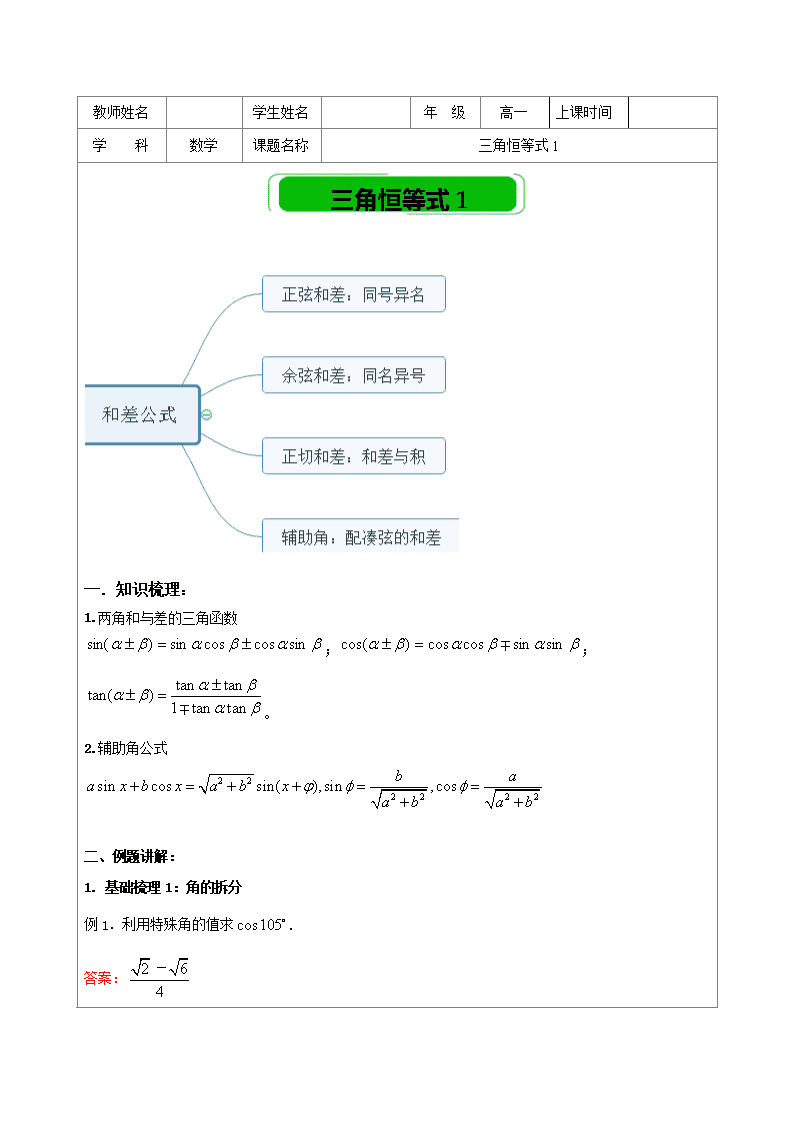
教师姓名 ‎ ‎ 学生姓名 ‎ ‎ 年 级 高一 上课时间 ‎ ‎ 学 科 数学 课题名称 三角恒等式1 ‎ 三角恒等式1‎ 一．知识梳理：‎ ‎1.两角和与差的三角函数 ‎；； 。‎ ‎2.辅助角公式 二、例题讲解：‎ ‎1. 基础梳理1：角的拆分 例1．利用特殊角的值求.‎ 答案：‎ 例2．求下列各式的值：‎ ‎（1） （2）tan17°+tan28°+tan17°tan28° 答案：（1） （2）1‎ ‎（3）(1+tan1°)(1+tan2°)(1+tan3°)……(1+tan44°)‎ 答案： 222‎ ‎（4）tan20°tan30°＋tan30°tan40°＋tan40°tan20°‎ 答案：1‎ ‎2. 基础梳理2： 公式应用 ‎（备注：）‎ 例3．利用两角和与差的正弦余弦公式证明tan（α＋β）＝ ‎ 答案：证明：tan（α＋β）＝＝＝.‎ 例4．求值 ‎（1）. （2）‎ 答案：（1） （2）‎ 例5．在中，如果，则为 （ ）‎ A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 锐角或直角三角形 答案：A ‎3. 难点分析1：角的变形 例6．已知cos+sin=,则sin的值是 .‎ 答案：‎ 例7． 已知sina=，，cosb=，，求cos(a-b)的值 答案： ‎ 例8．‎ 答案： ‎ 例9．在△ABC中，已知cosA =，cosB =，求cosC的值 答案： ‎ 例10．已知cos(2α-β)=-,sin (α-2β)=,且<α<,0<β<,求cos(α+β)的值 ‎ 答案：sin (2α-β)=; cos(α-2β)= ∴cos(α+β)= ‎ 例11．已知 答案： ‎ 例12． 已知，，，， 求sin(a + b)的值 答案： ‎ 例13．已知，，，求：、。‎ 答案：；‎ ‎【解析】∵，∴，。‎ 又∵，，‎ ‎∴，。‎ 例14．已知求的值.‎ 答案：‎ 例15．已知，且，求的值.‎ 答案：‎ ‎【解析】‎ ‎4.难点分析2： 公式变形 ‎（备注：）‎ 例16．求值 答案：‎ 例17．在中，求证：‎ 答案：证明：‎ ‎, ‎ 例18．已知，且满足关系式，则=______. ‎ 答案：‎ 例19．已知，则的取值范围是__________. ‎ 答案：‎ ‎【解析】令，① ，② 由①2+②2，得. ∴∈［-2,2］. ∴‎ ‎5. 辅助角 ‎（备注：）‎ 例20．利用辅助角公式化简(1) (2)‎ 答案：（1），（2）（3）‎ ‎ (5)‎ 答案：（4）（5） ‎ 例21．若，则实数的取值范围是__________‎ 答案：‎ 例22．已知：实数、满足，求证：。‎ 答案：证明：∵，∴，同理.‎ 设，；，‎ 代入，得＝1，‎ 即： ∵，，∴‎ 因此∴.‎ ‎6.综合应用 ‎（备注：）‎ 例23．如果是方程的两根,则____________.‎ 答案：‎ ‎【解析】‎ 则.‎ 例24．函数的最大值是( )‎ A. B.17 C.13 D.12‎ 答案：C ‎1．已知,tan(α+β)=1,且α是第二象限角,那么tanβ的值等于_____________.‎ 答案：-7‎ ‎【解析】∵,α是第二象限角,‎ ‎∴.∴.∴tanβ=tan［(α+β)-α］.‎ ‎2．求的值为__________. ‎ 答案：‎ ‎3．＝ ‎ 答案：－‎ ‎4．= ‎ 答案：‎ ‎5．(1＋tan10°)·（1＋tan35°）＝ ‎ 答案：2‎ ‎6．在△ABC中，tanA＝，tanB＝－2，则C＝ ‎ 答案：‎ ‎7．若tanAtanB＝tanA＋tanB＋1，则cos（A＋B）的值为( )‎ 答案：C ‎8．已知，，，求的值.‎ 答案：‎ ‎【解析】 ∵, ∴∴‎ ‎∴ 又 ∴‎ ‎∴sin2a=‎ ‎=‎ ‎9．下列四个命题中假命题是（ ）‎ A.存在这样的，使得 B.不存在无穷多个，使得 C.对于任意的，‎ D.不存在这样的，使得 答案：B ‎10．对任意的锐角，下列不等关系中正确的是（ ） ‎ A. B.‎ C. D.‎ 答案：C ‎11．已知tan（α＋β）＝，tan（β－）＝，求tan（α＋）‎ 答案：‎