- 2021-06-24 发布 |
- 37.5 KB |
- 8页

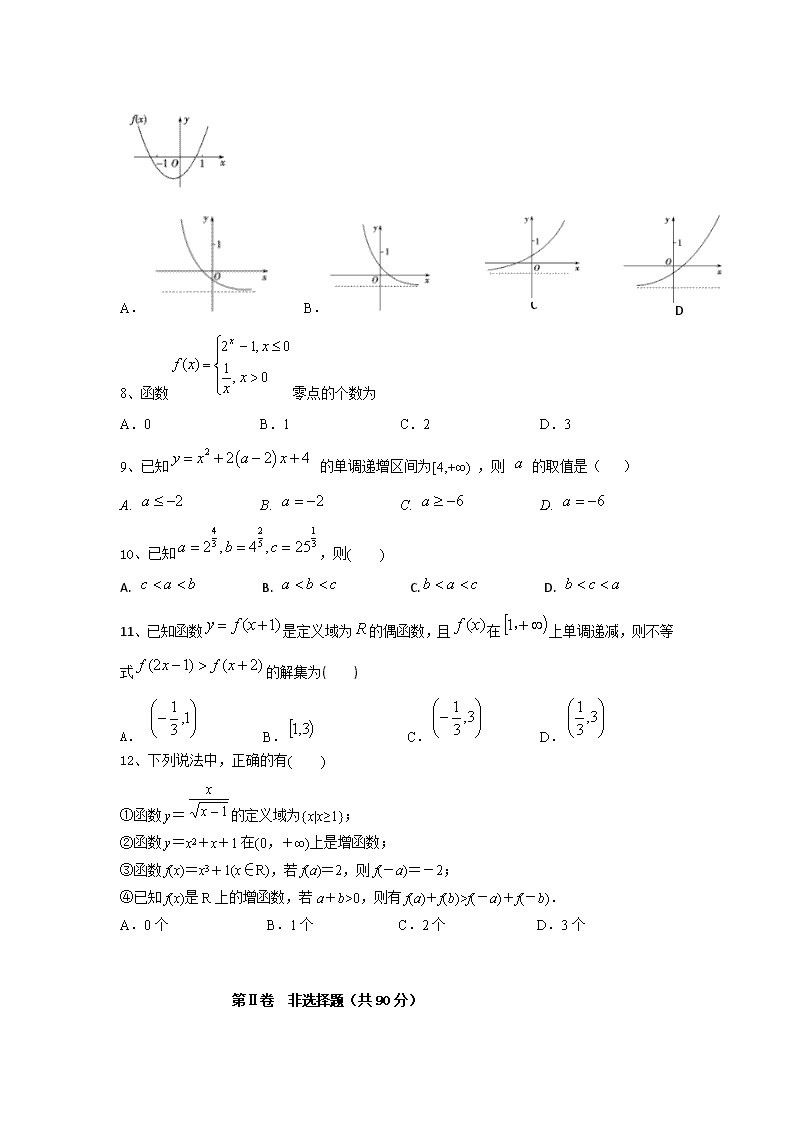

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年辽宁省大连渤海高级中学高一上学期期中考试数学试题
2018-2019学年辽宁省大连渤海高级中学高一上学期期中考试数学试题 考试时间:120分钟 试题满分:150分 考查范围:必修1 第一章、第二章,第三章指数函数及逻辑用语 第Ⅰ卷 选择题(共60分) 选择题(每题5分,共60分,将正确的答案选项填在答题卡上) 1、设全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则( ) A{0,1,3} B{1,3} C{1,2,3} D {0,1,2,3} 2、已知集合A={a,b},那么集合A的所有子集为( ). A.{a},{b} B.{a,b} C.{a},{b},{a,b} D. ∅,{a},{b},{a,b} 3、函数,的值域为( ) A.R B.[0,1] C.[2,5] D.[5,+∞) 4、已知p是r的充分条件,q是r的必要条件,那么p是q的( ) A.充分条件 B.必要条件 C.充要条件 D.既不充分也不必要条件 5、.给出下列命题: (1)有的四边形是菱形; (2)有的三角形是等边三角形; (3)无限不循环小数是有理数; (4)∀x∈R,x>1; (5)0是最小的自然数. 其中假命题的个数为( ) A.1 B.2 C.3 D.4 6、下列四个函数中,在(-∞,0]上为减函数的是( ) A. B. C. D. 7、已知函数(其中)的图象如下图所示,则函数的图象是( ) D C A. B. 8、函数零点的个数为 A.0 B.1 C.2 D.3 9、已知 的单调递增区间为[4,+∞) ,则 的取值是( ) A. B. C. D. 10、已知,则( ) A. B. C. D. 11、已知函数是定义域为的偶函数,且在上单调递减,则不等式的解集为( ) A. B. C. D. 12、下列说法中,正确的有( ) ①函数y=的定义域为{x|x≥1}; ②函数y=x2+x+1在(0,+∞)上是增函数; ③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2; ④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b). A.0个 B.1个 C.2个 D.3个 第Ⅱ卷 非选择题(共90分) 一、 填空题(每题5分,共20分,将正确答案写在答题卡上) 13、命题?°,?±的否定为 14、若函数,则 . 15、当a>0且a?ù1时,函数必过定点 16、关于x的方程4x﹣k•2x+k+3=0,只有一个实数解,则实数k的取值范围是 二、 解答题(17题 10分,18、19、20、21、22每题12分,将完整规范的解答过程写在答题卡上,必要的加以文字说明) 17、 (本题10分)计算下列各式 (1) (2) (结果为分数指数幂) 18、 (本题12分) 已知集合, . (?)当时,求; (?)若,求实数的取值范围. 19、 (本题12分) 求下列函数的定义域 (1); (2) 17、 (本题12分) 已知函数的图象过点(0,1),(-1,). (1)求m,n的值,并判断函数的奇偶性; (2)证明函数在[0,+∞)上是减函数; (3)若,求实数的取值范围 21、(本题12分) 已知函数. (?é?)若,求的值. (?騰)若函数在上的最大值与最小值的差为,求实数的值. 22、(本题12分) 已知二次函数满足,且。 (1)求的解析式; (2)当时,不等式恒成立,求实数的取值范围; (3)设,,求的最大值。 高一数学答案 一、 选择题 1- --5 BDCAB 6---10 AABBC 11--12 DC 二、 填空题 13、 14、 -- 1 15、(2,-2). 16、(﹣∞,﹣3)∪{6} 三、 解答题 17 (1)原式=0.4-1-1+(-2)-4+2-3=-1++=. 18、(1)时,可以求出集合-----------1分 --------------------3分 -------------------6分 (2)∵集合, 且, 所以,--------------8分 解之得,-----------10分 即实数的取值范围是. ------------12分 19、(1)要使函数有意义,只需…………2分 …………4分 所以定义域为 ………… 6分(不写成集合形式扣1分) (2)要使函数有意义,只需…………8分 …………10分 所以定义域为…………12分(不写成集合形式扣1分) 20、 其他方法也给分 21、(?é?)??,, ?à,解得:或, 当时,,, 当时,,, 故. (?騰)当时,在上单调递增, ?à,化简得, 解得:(舍去)或. 当时,在上单调递减, ?à,化简得. 解得:(舍去)或. 综上,实数的值为或. 22、(1)设,代入和, 并化简得,。 4分 (2)当时,不等式恒成立即不等式恒成立, 令,则,当时,,。 8分 (3)对称轴是。------------9分 ?é¨′当时,即时,;-------------10分 ?é¨2当时,即时, ----------------11分 综上所述:。 -----------------12分查看更多