2020届二轮复习逻辑联结词与种命题课件（全国通用）

2020届二轮复习逻辑联结词与种命题课件（全国通用）

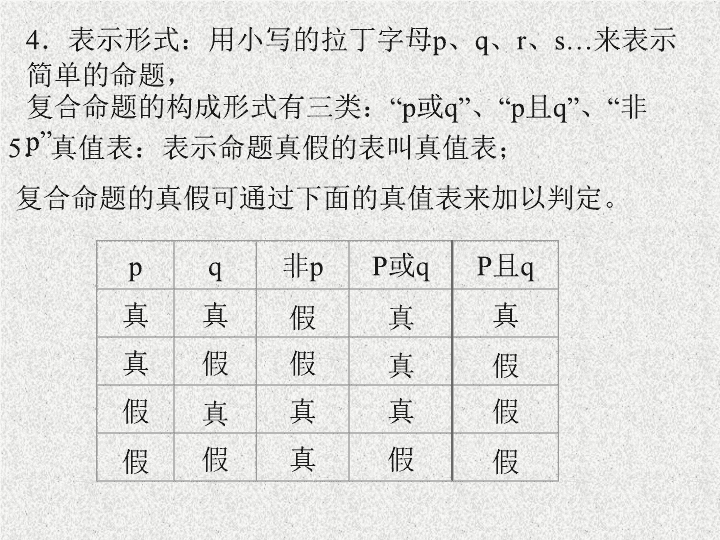
逻辑联结词与四种命题 高三备课组 一、基础知识 （一）逻辑联结词 1．命题：可以判断真假的语句叫做命题. 2．逻辑联结词：“或” “且” “非”这些词叫做逻辑联结词。 或：两个简单命题至少一个成立 且：两个简单命题都成立， 非：对一个命题的否定 3 ．简单命题与复合命题：不含逻辑联结词的命题叫做 简单命题 ；由简单命题与逻辑联结词构成的命题叫做 复合命题 。 5． 真值表：表示命题真假的表叫真值表； 复合命题的真假可通过下面的真值表来加以判定。 4．表示形式：用小写的拉丁字母 p、q、r、s… 来表示简单的命题， 复合命题的构成形式有三类： “ p 或 q” 、 “p 且 q” 、 “ 非 p” p q 非 p P 或 q P 且 q 真 真 假 真 真 真 假 假 真 假 假 真 真 真 假 假 假 真 假 假 （二）四种命题 1．一般地，用 p 和 q 分别表示原命题的条件和结论，用 ┐ p 和┐ q 分别表示 p 和 q 的否定。于是四种命题的形式为： 原命题：若 p 则 q（ ） 逆命题：若 q 则 p 否命题：若┐ p 则┐ q 逆否命题：若┐ q 则┐ p 2．四种命题的关系 ： 互 逆 原命题 若 p 则 q 逆命题 若 q 则 p 否命题 若 则 逆否命题 若 则 互 为 为 互 否 逆 逆 否 互 否 互 否 互 逆 3．一个命题的真假与其它三个命题的真假有如下四条关系： （1）原命题为真，它的逆命题不一定为真。 （2）原命题为真，它的否命题不一定为真。 （3）原命题为真，它的逆否命题一定为真。 （4）逆命题为真，否命题一定为真。 （三）几点说明 1．逻辑联结词“或”的理解是难点，“或”有三层含义： 以“ P 或 q” 为例：一是 p 成立但 q 不成立，二是 p 不成立但 q 成立，三是 p 成立且 q 成立， 2．对命题的否定只是否定命题的结论，而否命题既否定题设又否定结论 3．真值表 P 或 q：“ 一真为真”， P 且 q：“ 一假为假” 4．互为逆否命题的两个命题等价，为命题真假判定提供一个策略。 例1．已知复合命题形式，指出构成它的简单命题， （1）等腰三角形顶角的角平分线垂直平分底边， （2）垂直于弦的直径平分这条弦且平分弦所对的两条弧， （3） （4）平行四边形不是梯形 （ 1 ） P 且 q 形式，其中 p ： 等腰三角形顶角的角平分线垂直底边， q ： 等腰三角形顶角的角平分线平分底边； （2） P 且 q 形式，其中 p： 垂直于弦的直径平分这条弦， q： 垂直于弦的直径平分这条弦所对的两条弧 （3） P 或 q 形式，其中 p：4＞３，q：４＝３ （4）非 p 形式：其中 p： 平行四边形是梯形。 练习1.分别写出下列各组命题构成的“ p 或 q”、“p 且 q”、“ 非 p” 形式的复合命题 （1） p： 是有理数， q： 是无理数 （2） p： 方程 x 2 +2x-3=0 的两根符号不同， q： 方程 x 2 +2x-3=0 的两根绝对值不同。 （1） p： 是有理数， q： 是无理数 （ 2 ） p ： 方程 x 2 +2x-3=0 的两根符号不同， q ： 方程 x 2 +2x-3=0 的两根绝对值不同 例2．（四种命题之间的关系） 写出下列命题的 逆命题、否命题、逆否命题，并判断它们的真假。 （1） 已知 为实数，若 ，则 有两个不相等的实根； （2）若 ab=0， 则 a=0 或 b=0， （3） 若 x 2 +y 2 =0， 则 x 、y 全为零。 练习2.判断下列命题的真假，并写出它的 逆命题、否命题、逆否命题，同时判断这些命题的真假 （1）若 ab≤0， 则 a≤0 或 b≤0, （2） 若 a>b， 则 ac 2 >bc 2 （3） 若在二次函数 y=ax 2 +bx+c 中 b 2 -4ac<0 ， 则该二次函数图象与 x 轴有公共点。 例3． 已知命题 有两个不等的负根；命题 无实根 . 若命题 p 与命题 q 有且只有一个为真，求实数 m 的取值范围 . 练习3.已知下列三个方程： x 2 +4ax-4a+3=0 x 2 +(a-1)x+a 2 =0 x 2 +2ax-2a=0 至少有一个方程有实根，求实数 a 的取值范围。 小结 1．逻辑联结词“或”、“且”、“非”的意义与日常生活中的“或”、“且”、“非”的意义不尽相同。 要注意集合中的“并”、“交”、“补”的理解。 2．常用词语的否定 正面词 都是 任意的 所有的 至多有一个 至少有一个 反面词 不都是 某个 某些 至少有两个 一个也没有 3．等价命题：原命题 它的逆否命题 原命题的否命题 原命题的逆否命题 作业 优化设计 P 5 　 闯关训练