通州区2018-2019学年第一学期高三年级期末考试数学（理科）试卷

通州区2018-2019学年第一学期高三年级期末考试数学（理科）试卷

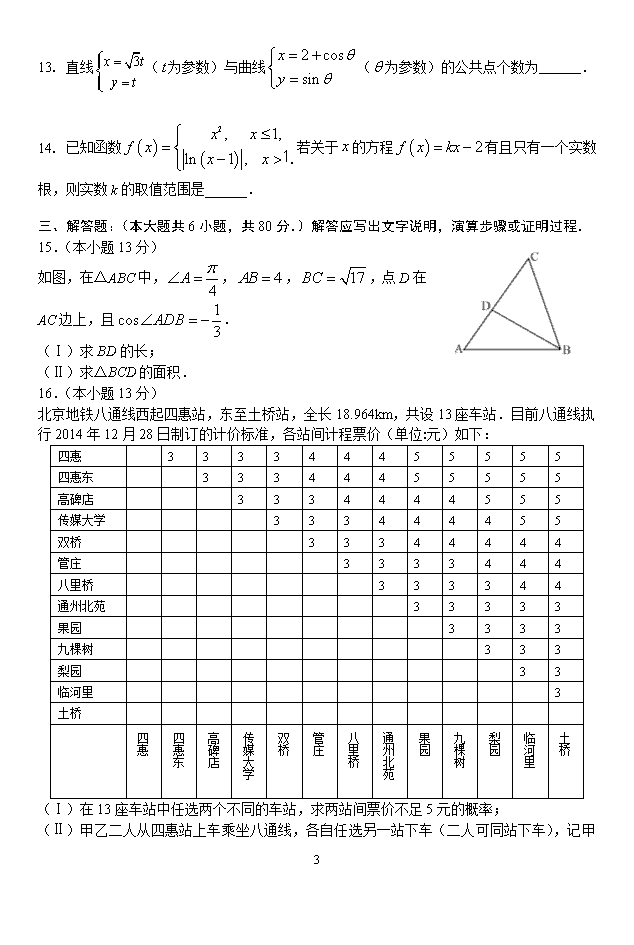
通州区2018-2019学年第一学期高三年级期末考试 数学（理科）试卷 ‎2019年1月 考生须知 ‎1.本试卷共4页，满分150分．考试时长120分钟．‎ ‎2.本试卷分为第一部分和第二部分两部分．‎ ‎3.考生务必将答案答在答题卡上，在试卷上作答无效．‎ ‎4 .考试结束后，将试卷和答题卡一并交回．‎ 第一部分（选择题 共40分）‎ 一、选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 设集合,，则 A. B. C. D. ‎2. 设向量，,则与垂直的向量的坐标可以是 A. B. C. D. ‎ ‎3.已知是定义在R上的奇函数，且当时，，则等于 A. B. C. D. 3 ‎4.已知双曲线的右焦点与抛物线的焦点重合，则a等于 A.1 B. 2 C. 3 D. ‎ ‎5. 已知x,y满足不等式组则的最大值等于 A. B. C. D. ‎ ‎6. 设，则“ ”是“”的 5‎ A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 ‎7.某四棱锥的三视图如图所示，在此四棱锥的侧面中，面积最小的侧面面积为 A. 1 B. C. 2 D. ‎ ‎8.设函数图象上不同两点，处的切线的斜率分别是，，规定 （为线段的长度）叫做曲线在点与点之间的“弯曲度”，给出以下命题：‎ ‎①函数图象上两点与的横坐标分别为和，则； ‎ ‎②存在这样的函数，其图象上任意不同两点之间的“弯曲度”为常数；‎ ‎③设,是抛物线上不同的两点，则；‎ ‎④设,是曲线（是自然对数的底数）上不同的两点，则．‎ 其中真命题的个数为 A. 1 B.2 C.3 D. 4‎ 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9.复数的共轭复数是______． ‎ ‎10.设等比数列{an}的公比，前n项和为，则______ ．‎ ‎11. 已知角的终边与单位圆的交点为，则 ． ‎ ‎12.的展开式中含的项的系数是______．‎ 5‎ ‎13. 直线（为参数）与曲线（为参数）的公共点个数为______．‎ ‎14. 已知函数若关于的方程有且只有一个实数根，则实数k的取值范围是______．‎ 三、解答题：（本大题共6小题，共80分．）解答应写出文字说明，演算步骤或证明过程．‎ ‎15．（本小题13分）‎ 如图，在△ABC中，，，，点D在AC边上，且．‎ ‎（Ⅰ）求BD的长；‎ ‎（Ⅱ）求△BCD的面积．‎ ‎16．（本小题13分）‎ 北京地铁八通线西起四惠站，东至土桥站，全长18.964km，共设13座车站．目前八通线执行2014年12月28日制订的计价标准，各站间计程票价（单位:元）如下：‎ 四惠 ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ 四惠东 ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ 高碑店 ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎5‎ ‎5‎ 传媒大学 ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎5‎ 双桥 ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎4‎ ‎4‎ 管庄 ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ 八里桥 ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ 通州北苑 ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ 果园 ‎3‎ ‎3‎ ‎3‎ ‎3‎ 九棵树 ‎3‎ ‎3‎ ‎3‎ 梨园 ‎3‎ ‎3‎ 临河里 ‎3‎ 土桥 四惠 四惠东 高碑店 传媒大学 双桥 管庄 八里桥 通州北苑 果园 九棵树 梨园 临河里 土桥 ‎（Ⅰ）在13座车站中任选两个不同的车站，求两站间票价不足5元的概率；‎ 5‎ ‎（Ⅱ）甲乙二人从四惠站上车乘坐八通线，各自任选另一站下车（二人可同站下车），记甲乙二人乘车购票花费之和为X元，求X的分布列；‎ ‎（Ⅲ）若甲乙二人只乘坐八通线，甲从四惠站上车，任选另一站下车，记票价为元；乙从土桥站上车，任选另一站下车，记票价为元．试比较和的方差和大小．（结论不需要证明）‎ ‎17．（本小题14分）‎ 如图，在三棱柱中，底面，△ABC是边长为的正三角形，，D，E分别为AB，BC的中点． ‎ ‎（Ⅰ）求证：平面； ‎ ‎（Ⅱ）求二面角的余弦值；‎ ‎（Ⅲ）在线段上是否存在一点M，使平面？说明理由.‎ ‎18．（本小题14分）‎ 已知椭圆：过点，且椭圆的离心率为．‎ ‎ (Ⅰ)求椭圆的方程；‎ ‎(Ⅱ)斜率为的直线交椭圆于，两点，且．若直线上存在点P，使得是以为顶角的等腰直角三角形，求直线的方程．‎ ‎19．（本小题13分）‎ 已知函数，其中．‎ ‎（Ⅰ）求的单调区间；‎ ‎（Ⅱ）设，若曲线，有公共点，且在点处的切线相同，求的最大值．‎ ‎20．（本小题13分）‎ 一个大于1的自然数，除了1和它本身外，不能被其他自然数整除，则称这个数为质数．质数的个数是无穷的．设由所有质数组成的无穷递增数列的前项和为，等差数列1，3，5，7，…中所有不大于的项的和为．‎ 5‎ ‎（Ⅰ）求和； ‎ ‎(Ⅱ) 判断和的大小，不用证明；‎ ‎（Ⅲ）设，求证：，，使得．‎ 5‎