2017-2018学年安徽省滁州市定远县育才学校高二（实验班）下学期第三次月考数学（理）试题（Word版）

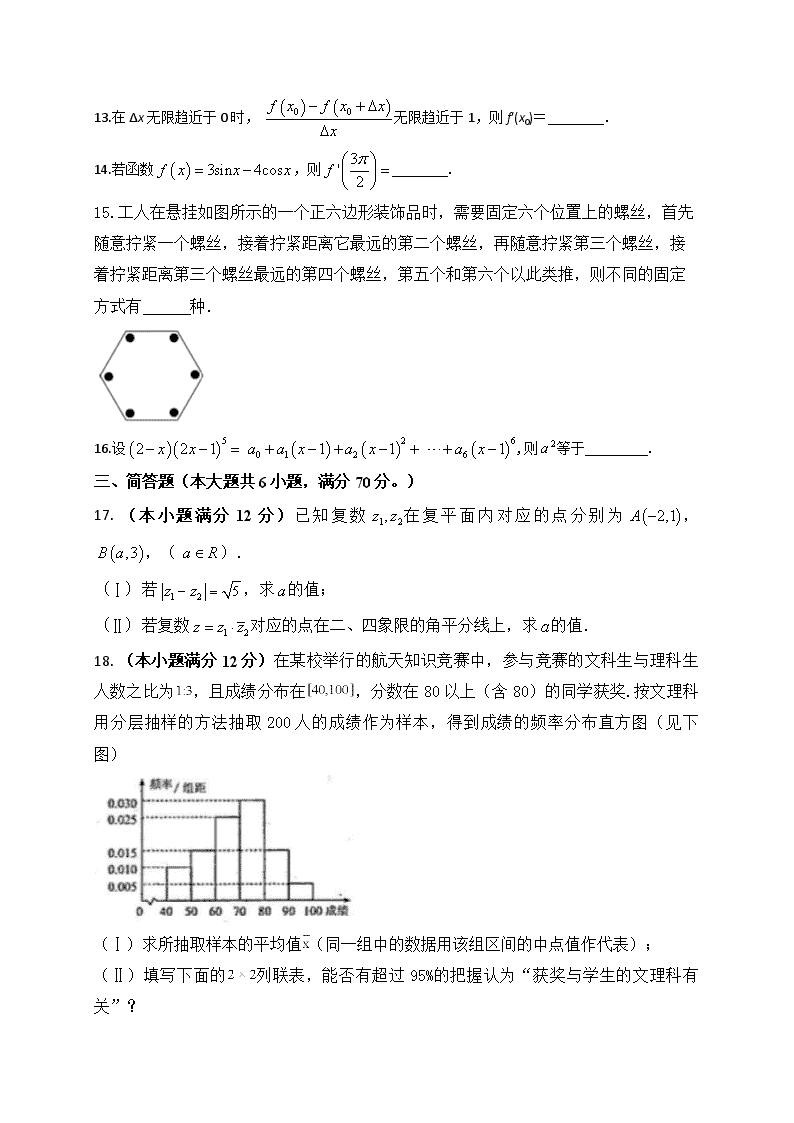
2017-2018学年安徽省滁州市定远县育才学校高二（实验班）下学期第三次月考数学（理）试题（Word版）

‎2017-2018学年安徽省滁州市定远县育才学校高二（实验班）下学期第三次月考理科数学 ‎ 全卷满分150分，考试用时120分钟 第I卷（选择题 60分）‎ 一、 选择题（本大题共12小题，每小题5分，共60分）‎ ‎1.在 的展开式中， 项的系数为（ ） A.28 B.56 C.-28 D.-56‎ ‎2.的值为 ( ) A.0 B.1 C. D.‎ ‎3.在1，2，3，4，5，6，7，8这组数据中，随机取出五个不同的数，则数字4是取出的五个不同数的中位数的概率为( )‎ A. B. C. D. ‎ ‎4.已知随机变量服从正态分布即，且，若随机变量，则（ ）‎ A. 0.3413 B. 0.3174 C. 0.1587 D. 0.1586‎ ‎5.若为虚数单位， ，且，则复数的模等于( )‎ A. B. C. D. ‎ ‎6.已知函数，若，则的值等于（ ）‎ A. B. C. D. ‎ ‎7.根据给出的数塔猜测（ ）‎ ‎…‎ A. B. C. D. ‎ ‎8.若曲线存在与直线垂直的切线，则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎9.函数的导函数的大致图象如图所示，则函数的图象可能是（　　）‎ A. B. C. D. ‎ ‎10.根据如下样本数据得到的回归方程为，若，则每增加1个单位，就（ ）‎ A. 增加0.9个单位 B. 减少0.9个单位 C. 增加1个单位 D. 减少1个单位 ‎11.复数满足，若复数，在平面直角坐标系中对应的点为，则点到直线的距离为( )‎ A. B. C. D. ‎ ‎12.如图放置的边长为1的正方形PABC沿轴滚动，点B恰好经过原点．设顶点的轨迹方程是，则 ( )‎ A. B. C. D. ‎ 第II卷（非选择题 90分）‎ 二、填空题（本大题共4小题，每小题5分，满分20分。）‎ ‎13.在Δx无限趋近于0时， 无限趋近于1，则f′(x0)＝________．‎ ‎14.若函数，则________.‎ ‎15.工人在悬挂如图所示的一个正六边形装饰品时，需要固定六个位置上的螺丝，首先随意拧紧一个螺丝，接着拧紧距离它最远的第二个螺丝，再随意拧紧第三个螺丝，接着拧紧距离第三个螺丝最远的第四个螺丝，第五个和第六个以此类推，则不同的固定方式有   种． ‎ ‎16.设 ,则等于_________.‎ 三、简答题（本大题共6小题，满分70分。）‎ ‎17. （本小题满分12分）已知复数在复平面内对应的点分别为， ，（ ）． ‎ ‎（Ⅰ）若，求的值； ‎ ‎（Ⅱ）若复数对应的点在二、四象限的角平分线上，求的值．‎ ‎18. （本小题满分12分）在某校举行的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为，且成绩分布在，分数在80以上（含80）的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本，得到成绩的频率分布直方图（见下图）‎ ‎（Ⅰ）求所抽取样本的平均值（同一组中的数据用该组区间的中点值作代表）；‎ ‎（Ⅱ）填写下面的列联表，能否有超过95%的把握认为“获奖与学生的文理科有关”？‎ 附表及公式：‎ ‎，其中 ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎19. （本小题满分12分）数列满足，前n项和．‎ ‎（1）写出；‎ ‎（2）猜出的表达式，并用数学归纳法证明．‎ ‎20. （本小题满分12分）已知函数.‎ ‎（Ⅰ）求曲线在点处的切线方程.‎ ‎（Ⅱ）求的单调区间.‎ ‎（Ⅲ）求在上的最大值和最小值.‎ ‎21. （本小题满分12分）某地高中年级学生某次身体素质体能测试的原始成绩采用百分制，已知这些学生的原始成绩均分布在内，发布成绩使用等级制，各等级划分标准见下表，并规定： 三级为合格， 级为不合格 为了了解该地高中年级学生身体素质情况，从中抽取了名学生的原始成绩作为样本进行统计，按照分组作出频率分布直方图如图所示，样本中分数在分及以上的所有数据的茎叶图如图所示.‎ ‎(Ⅰ) 求及频率分布直方图中的值；‎ ‎(Ⅱ) 根据统计思想方法，以事件发生的频率作为相应事件发生的概率，若在该地高中学生中任选人，求至少有人成绩是合格等级的概率；‎ ‎(Ⅲ)上述容量为的样本中，从两个等级的学生中随机抽取了名学生进行调研，记为所抽取的名学生中成绩为等级的人数，求随机变量的分布列及数学期望.‎ ‎22. （本小题满分10分）某地区预计从2015年初开始的第月，商品的价格（， ，价格单位：元），且第月该商品的销售量（单位：万件）.‎ ‎（1）商品在2015年的最低价格是多少？‎ ‎（2）2015年的哪一个月的销售收入最少，最少是多少？‎ 参考答案解析 ‎1.A ‎2.C ‎3.B ‎4.C ‎5.C ‎6.C ‎【解析】 ,选C.‎ ‎7.B ‎【解析】7.由1×9+2=11；‎ ‎12×9+3=111；‎ ‎123×9+4=1111；‎ ‎1234×9+5=11111；‎ ‎…‎ 归纳可得：等式右边各数位上的数字均为1，位数跟等式左边的第二个加数相同，‎ ‎∴123456×9+7=1111111，‎ 本题选择B选项.‎ ‎8.C[]‎ ‎【解析】函数， ，则，若函数存在与直线垂直的切线，可得有大于0的解，则，解得，则实数的取值范围是，故选C.‎ ‎9.B ‎【解析】由导函数的大致图象如图所示可得，导函数的符号为负，正，负，正；对应函数的单调性为：减函数，增函数，减函数，增函数．极值点两个大于0，一个小于0，故选B.‎ ‎10.B ‎【解析】由题意可得，，回归方程为，若，且回归直线过点，，解得每增加一个单位，就减少个单位，故选B.‎ ‎11.B ‎【解析】由题意得，，M(4,3),根据点到直线距离，选B.‎ ‎12.B ‎【解析】 ，故选B.‎ ‎13.‎ ‎【解析】由已知得Δx无限趋近于0时，， 无限趋近于－1，‎ 则f′(x0)＝－1.‎ 答案：－1‎ ‎14.‎ ‎【解析】‎ ‎15.2880‎ ‎【解析】第一阶段：先随意拧一个螺丝，接着拧它对角线上的，有 种方法；再随意拧第三个螺丝，和其对角线上的，有 种方法；然后随意拧第五个螺丝，和其对角线上的，有 种方法． 第二阶段：先随意拧一个螺丝，有 种方法，完成上述过程分步进行；再随意拧不相邻的，若拧的是对角线上的，有 种方法；若拧的是不相邻斜对角线上的，则还有6种拧法，完成上述过程分类进行，所以总共的固定方式有： ×（4+6）=2880． 故答案为2880． 分两个阶段，利用组合知识求解即可．‎ ‎16.‎ ‎【解析】设，则，则．应填答案。‎ ‎17.（1）或（2）‎ ‎【解析】（1）根据复数的模可得方程，解得或（2）根据复数共轭及复数乘法得z= 在直线上，再根据复数几何意义得在直线上,列方程，解得 试题解析：解：（I）由复数的几何意义可知： ． ‎ 因为，所以 ．‎ 解得或 ‎（II）复数 ‎ 由题意可知点在直线上 所以，解得 ‎18.(Ⅰ)40；(Ⅱ)答案见解析.‎ ‎【解析】 (1)利用频率和为，求的值，利用同一组中的数据用该组区间的中点值作代表，计算所抽取样本的平均值；〔2〕利用公式求出与临界值比较，即可得出结论.‎ 试题解析：（Ⅰ） .‎ 文科生参赛人数（人）‎ 理科生参赛人数（人）‎ 优秀学生数（人）‎ ‎（Ⅱ）‎ ‎ ，‎ 所以有超过95%的把握认为“获奖与学生的文理科有关”.‎ ‎19.（1）， ， ；（2），证明见解析．‎ ‎【解析】（1）令，∵，∴，即，∴．‎ 令，得，即，∴．‎ 令，得，即，∴．‎ ‎（2）猜想，下面用数学归纳法给出证明．‎ ‎①当时， ，结论成立．‎ ‎②假设当时，结论成立，‎ 即，‎ 则当时， ，‎ ‎，即．‎ ‎∴，∴．‎ 当时结论成立．‎ 由①②可知，对一切都有．‎ ‎20.(Ⅰ) ；(Ⅱ)单调增区间为，单调减区间为．(Ⅲ) ‎ ‎， ．‎ ‎【解析】‎ ‎（I）∵，‎ ‎∴， ，‎ 所以切线方程为： ，‎ 即： ．‎ ‎（），‎ 令，得；‎ 令，得．‎ ‎∴单调增区间为，‎ 单调减区间为．‎ ‎（）时，‎ 在上单调递增，‎ 在上单调递减．‎ ‎∴，‎ ‎， ．‎ ‎∴，‎ ‎∴．‎ ‎21.（Ⅰ）；（Ⅱ） ；（Ⅲ）见解析.‎ ‎【解析】‎ ‎（Ⅰ）由题意知，样本容量 ‎（Ⅱ）样本中成绩是合格等级的人数为，成绩是合格等级的频率为，故从该校学生中任选人，成绩是合格等级的概率为，用表示事件“从该地高中学生中任选人，至少有人成绩是合格等级，则”‎ ‎（Ⅲ）样本中等级的学生人数为人， 等级的学生人数为人，故随机变量的所有取值 ‎ 于是随机变量的分布列为 所以， ‎ ‎22.（1）最低价格为16.5元；（2）第5月的销售收入最低.最低销售收入为289万元.‎ ‎【解析】（1）， 当时， 取得最小值，‎ 即第6月的价格最低，最低价格为16.5元；‎ ‎（2）设第月的销售收入为（万元），依题意有 ‎ ，‎ ‎ ，‎ 所以当时， 递减；‎ 当时， 递增，‎ 所以当时， 最小，即第5个月销售收入最少.最低销售收入为289万元.‎