江西省南昌市新建县第一中学2020届高三第三次适应性考试数学（理）试卷

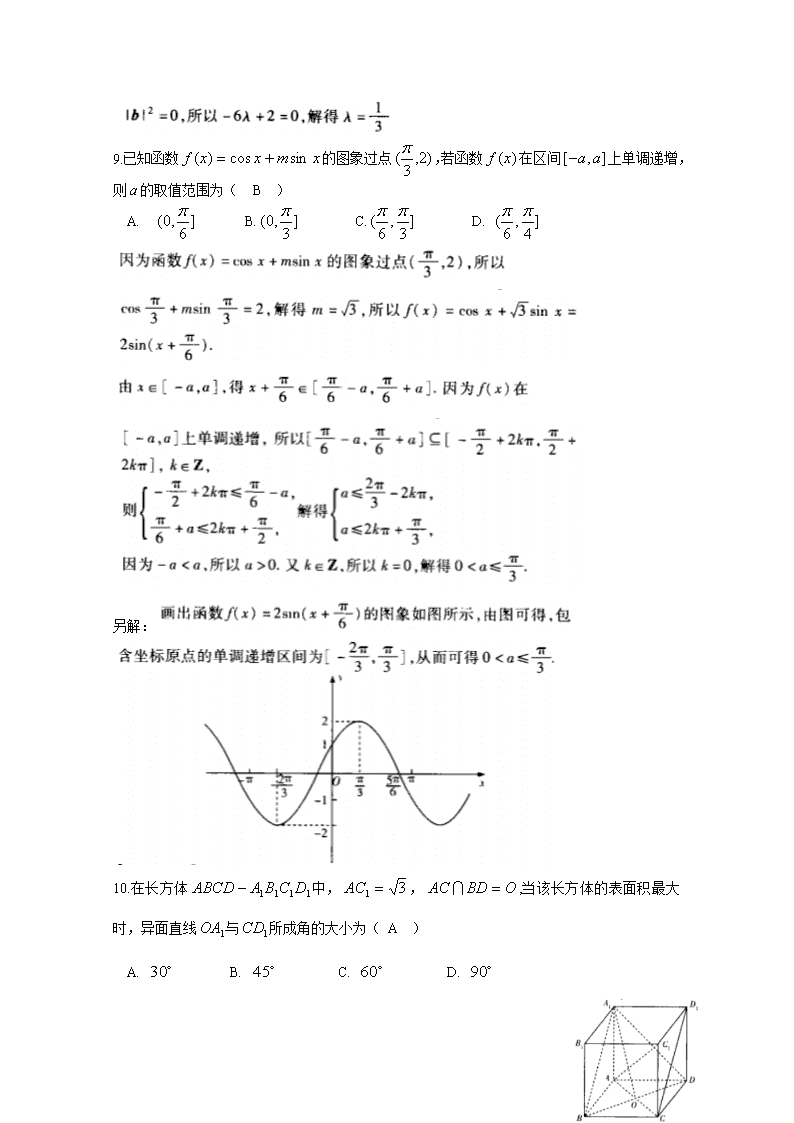
江西省南昌市新建县第一中学2020届高三第三次适应性考试数学（理）试卷

数学理科试卷 一、 选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ 1. 设集合，则满足条件的集合的个数是 （ C ）‎ A. ‎2 B. 3 C. 4 D. 16‎ ‎2.已知，则复数（ C ）‎ A. B. C. D. ‎ ‎3.已知双曲线(，)的顶点到渐近线的距离为，则该双曲线的离心率为( D )‎ A. B.2 C. D.‎ ‎4.已知对数函数的图像经过点与点，，，，则（ D ）‎ A. ‎ B. C. D. ‎ ‎5.刘徽（约公元225年—295年），魏晋期间伟大的数学家，中国古典数学理论的奠基人之一.他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的佳作.割元术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形（如图所示），当n变得很大时，这n个等腰三角形的面积之和近似等于圆的面积.运用割元术的思想，得到的近似值为（ A ）‎ A. ‎ B. C. D. ‎ ‎6.已知等差数列的通项公式为，当且仅当时，数列的前项和最大，则当时，（ A ）‎ A. ‎ 20 B. 21 C. 22 D. 23‎ ‎7.若函数的定义域为，则的单调递增区间为（ D ）‎ ‎ A. B. C. D. ‎ ‎ ‎ 8. 已知向量，向量在方向上的投影为，若，则实数的值为（ B ）‎ A. ‎ B. C. D. ‎ ‎9.已知函数的图象过点，若函数在区间上单调递增，则的取值范围为（ B ）‎ A. ‎ B. C. D. ‎ 另解：‎ ‎10.在长方体中，，,当该长方体的表面积最大时，异面直线与所成角的大小为（ A ）‎ A. ‎ B. C. D. ‎ ‎11.已知函数关于直线对称，函数 则下列四个命题中，真命题有（ C ）‎ ①的图象关于点成中心对称；‎ ②若对都有则的最小值为；‎ ③将的图象向左平移个单位，可以得到的图象；‎ ④，使得.‎ A. ①③ B. ②③ C. ①④ D. ②④‎ ‎12.若函数恰有两个零点，则实数的取值范围是（ A ）‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎13.2019年11月12日，中国人民银行发布双十一“剁手”数据，全国人民人均消费超过1000元，某调查机构调查该地区不同年龄段的人均消费情况，得到如图所示的扇形统计图。已知年龄小于25岁的人均消费为700元，则年龄在25~35岁之间的人均消费为 1600 元 ‎14.将满足约束条件的实数对所组成的集合记作D，设，则的取值范围是 。‎ ‎15.将一个表面积为的圆锥的侧面沿一条母线展开，得到一个圆心角为的扇形，则该圆锥的轴截面的面积= .‎ ‎ ‎ ‎ ‎ ‎16.已知双曲线：的上、下焦点分别为,过且垂直与轴的直线与交于两点，直线分别交轴于点，若,则过点的直线的斜率的最大值为 ，此时双曲线的离心率为 。‎ 三、解答题 ‎17.设为数列的前项和，已知，且.‎ ‎（1）求的通项公式；‎ ‎（2）若点在函数的图象上，求证：。‎ ‎ 18.如图，菱形中，，为中点，将沿折起使得平面平面 ，与相交于点，是棱上的一点且满足.‎ （1） 求证：平面；‎ （2） 求二面角的余弦值.‎ ‎19.2019年12月9日，记者走进浙江缙云北山村，调研“中国淘宝村”‎ 的真实模样，作为最早追赶电商大潮的中国村庄，地处浙中南偏远山区的北山村，是电商改变乡村、改变农民命运的生动印刻。互联网的通达，让这个曾经的空心村在高峰时期生长出400多家网店，网罗住500多位村民，销售额达两亿元。一网店经销缙云土面，在一个月内，每售出1t缙云土面可获利800元，未售出的缙云土面，每1t亏损500元。根据以往的销售统计，得到一个月内五地市场对缙云土面的需求量的频率分布直方图，如图所示，该网店为下一个月购进了100t缙云土面，用（单位：，）表示下一个月五地市场对缙云土面的需求量，（单位：元）表示下一个月该网店经销缙云土面的利润。‎ （1） 将表示为的函数；‎ （2） 根据直方图估计利润不少于67000元的概率；‎ （3） 在直方图的需求量分组中，同一组中的数据用该组区间的中点值为代表，将需求量落入该区间的频率作为需求量取该区间中点值时的概率（例如，若需求量，则取，且的概率等于需求量落入的频率），求该网店下一个月利润的分布列和期望值。‎ ‎20.已知椭圆的焦点为是椭圆C上一点，若椭圆C的离心率为，且的面积为.‎ ‎（1）求椭圆C的方程；‎ ‎（2）已知是坐标原点，向量，过点的直线与椭圆C交于M，N两点.若点满足,求的最小值.‎ ‎ 21.已知函数 ‎（1）若求函数的最大值；‎ ‎（2）设若对任意不等式恒成立，求实数的取值范围.‎ 22. 已知曲线的参数方程为，曲线的参数方程为 （1） 求曲线和曲线的普通方程；‎ （2） 过坐标原点作直线交曲线于点（异于点），交曲线于点，求的最小值.‎ ‎23.‎ 已知函数 （1） 若解关于的不等式；‎ （2） 若时，恒成立，求实数的取值范围.‎