2017-2018学年河北省巨鹿中学高二上学期第一次月考数学试题

2017-2018学年河北省巨鹿中学高二上学期第一次月考数学试题

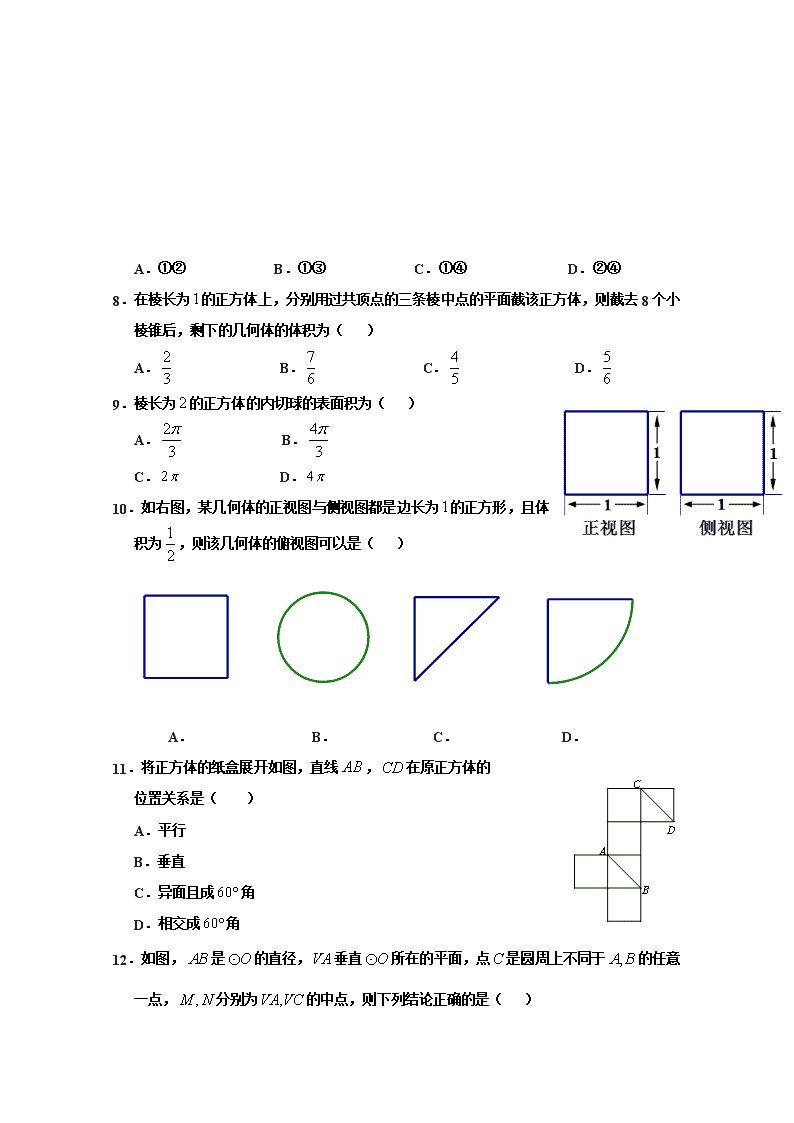
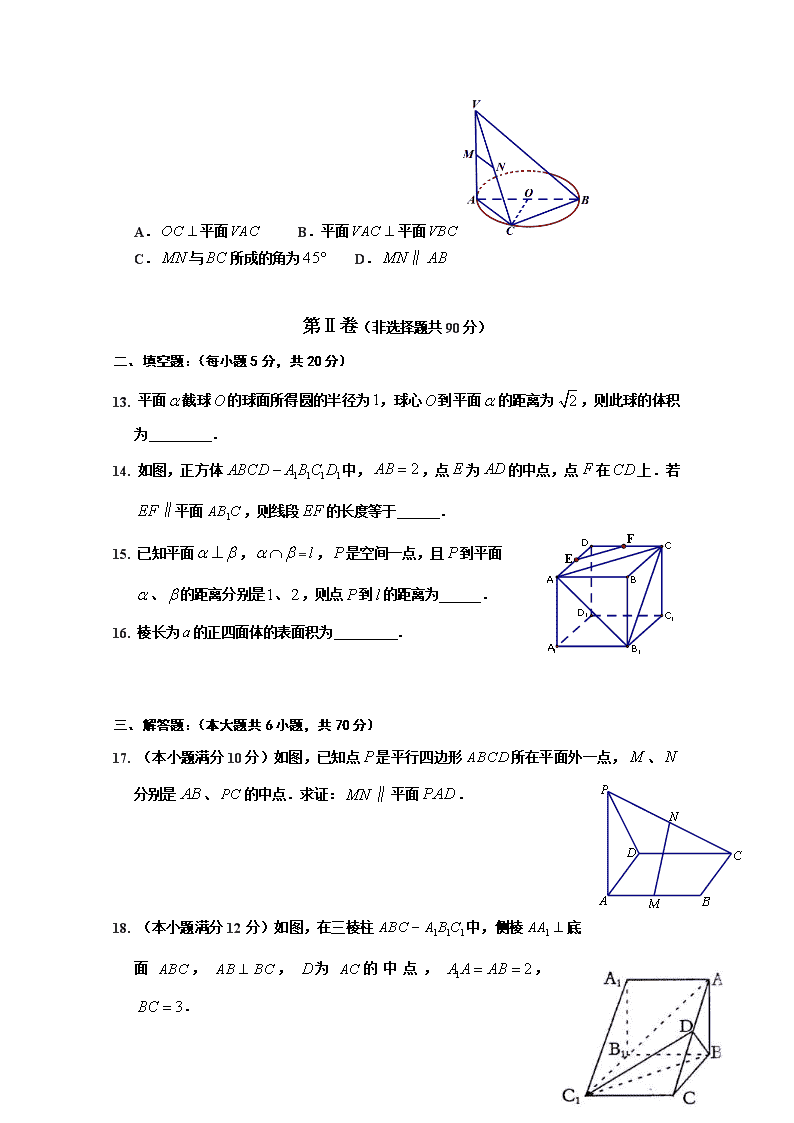
‎2017-2018学年河北省巨鹿中学高二上学期第一次月考数学试题 考试时间：120分钟 第Ⅰ卷（选择题共60分）‎ 一、选择题：（每小题５分，共60分）‎ ‎1．一个几何体的三视图中的一个视图是圆，则这个几何体不可能是（ ）‎ ‎ A．球 B．长方体 C．圆柱 D． 圆锥 ‎2．关于空间两条直线和平面，下列命题正确的是（ ）‎ ‎ A．若，则 B．若，则 C．若，则 D．若，则 ‎3．下面给出四个条件：① 空间三个点；② 一条直线和一个点；③ 和直线都相交的两条直线；④ 两两相交的三条直线．其中能确定一个平面的条件有（ ）‎ ‎ A．0个 B．1个 C．2个 D．3个 ‎4．若是异面直线，是异面直线，则和的位置关系是（ ）‎ ‎ A． B．和异面 C．和相交 D．以上选项均有可能 ‎5．在下列命题中，不是公理的是（ ）‎ ‎ A．平行于同一个平面的两个平面相互平行 B．过不在同一条直线上的三点，有且只有一个平面 C．如果一条直线上两点在一个平面内，那么这条直线上所有的点都在此平面内 D．如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 ‎6．下列命题中，真命题是（ ）‎ ‎ A．若一个平面经过另一个平面的垂线，那么这两个平面相互垂直 B．若一个平面经过另一个平面的平行线，那么这两个平面相互平行 C．若一条直线平行于一个平面，则这条直线平行于平面内的任意直线 D．若一条直线同时平行于两个不重合的平面，则这两个平面平行 ‎7．下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）‎ ‎①正方形 ‎②圆锥 ‎③三棱台 ‎④正四棱锥 A．①② B．①③ C．①④ D．②④‎ ‎8．在棱长为的正方体上，分别用过共顶点的三条棱中点的平面截该正方体，则截去8个小棱锥后，剩下的几何体的体积为（ ）‎ ‎ A． B． C． D． ‎9．棱长为的正方体的内切球的表面积为（ ）‎ ‎ A． B． ‎ ‎ C． D． ‎10．如右图，某几何体的正视图与侧视图都是边长为的正方形，且体积为，则该几何体的俯视图可以是（ ）‎ ‎ ‎ A． B． C． D．‎ ‎11．将正方体的纸盒展开如图，直线，在原正方体的 ‎ 位置关系是（　　） ‎ ‎ A．平行 ‎ ‎ B．垂直 C．异面且成角 ‎ D．相交成角 ‎12．如图，是的直径，垂直所在的平面，点是圆周上不同于的任意一点，分别为的中点，则下列结论正确的是（ ）‎ ‎ A．平面 B．平面平面 C．与所成的角为 D． 第Ⅱ卷（非选择题共90分）‎ 二、填空题：（每小题5分，共20分）‎ ‎13. 平面截球的球面所得圆的半径为，球心到平面的距离为，则此球的体积为 ．‎ ‎14. 如图，正方体中，，点为的中点，点在上．若平面，则线段的长度等于 ．‎ ‎15. 已知平面，=，是空间一点，且到平面 、的距离分别是、，则点到的距离为 ．‎ ‎16. 棱长为的正四面体的表面积为 ．‎ 三、解答题：（本大题共6小题，共70分）‎ ‎17. （本小题满分10分）如图，已知点是平行四边形所在平面外一点，、 分别是、的中点．求证：平面．‎ ‎18. （本小题满分12分）如图，在三棱柱中，侧棱底面，，为的中点，，．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求四棱锥的体积．‎ ‎19. （本小题满分12分）如图，四棱锥中，底面，，点在线段上，且．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）若，，，，求四棱锥的体积．‎ ‎20. （本小题满分12分）‎8‎ ‎6‎ 已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为，高为的等腰三角形，侧视图（或称左视图）是一个底边长为，高为的等腰三角形．‎ ‎（Ⅰ）求该几何体的体积；‎ ‎（Ⅱ）求该几何体的侧面积．‎ ‎21. （本小题满分12分）如图，在四棱锥中，底面，四边形 是直角梯形，，，，．‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求点到平面的距离．‎ ‎22. （本小题满分12分）如图，在边长为的正方形中，、分别为、 的中点，现在沿、及把、和折起，使、、三点重合，重合后的点记为，求：‎ ‎（Ⅰ）这个几何体每个面的三角形的面积；‎ ‎（Ⅱ）这个几何体的体积；‎ ‎（Ⅲ）点到平面的距离．‎ ‎2017—2018学年上学期第一次月考 高二年级试题参考答案与评分标准 一、选择题（每题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A D A A D A D C C B 二、填空题（每题5分，共20分）‎ ‎13. ; 14. ; 15. ; 16. .‎ 三、解答题：（本大题共6小题，共70分）‎ ‎17. （本题满分10分）证明：‎ 设的中点为，如右图，连接．‎ 点、分别为、的中点，‎ 在中，，且；‎ 点为的中点，‎ ，且，‎ ，且，‎ 四边形为平行四边形，‎ ，‎ 又平面，平面，‎ 平面． …………………10分 另证：取的中点，证明平面平面，进而得平面．‎ ‎18. （本题满分12分）解：‎ ‎（Ⅰ）证明：连接交于点，连接．‎ ‎∵ 在中，分别为的中点，‎ ‎∴ ．‎ ‎∵ 平面，平面，‎ ‎∴ 平面； …………………4分 ‎（Ⅱ）过点做交于点．‎ ‎∵ 侧棱底面，‎ ‎∴ ，‎ ‎∴ 平面，即为四棱锥的高．…………………6分 ‎ 中，． …………………8分 ‎ 直角梯形中，，‎ ‎∴ 梯形的面积． …………………10分 ‎∴ 四棱锥的体积． …………………12分 ‎19. （本题满分12分）解：‎ ‎（Ⅰ）证明：∵ 底面，‎ ‎∴ ．‎ ‎∵ ，‎ ‎∴ 平面． …………………4分 ‎∵ ，‎ ‎∴ 平面； …………………6分 ‎（Ⅱ）中，，，，‎ ‎∴ ，， …………………8分 ‎∵ ，，，，，‎ ‎∴ 矩形的面积为， …………………10分 ‎∴ 四棱锥的体积． …………………12分 ‎20. （本题满分12分）解：‎ ‎（Ⅰ）； …………………6分 ‎（Ⅱ） ． …………………12分 ‎21. （本题满分12分）解：‎ ‎（Ⅰ）∵ PA平面PBCD,BC平面PBCD ，‎ ‎∴ PABC ,‎ 又∵ABBC ，PAAB=A，‎ ‎∴ BC平面PAB，‎ ‎∵ BC平面PBC，‎ ‎∴ 平面⊥平面； …………………6分 ‎(2), ∵ , ‎ 设点C到平面PBD的距离为,‎ ‎∵ ，‎ ‎ ∴ ,‎ ‎∴ ，即点C到平面PBD的距离为． …………………12分 ‎22. （本题满分12分）解：折起后的几何体如图所示．‎ ‎（Ⅰ）由、分别是、边的中点可得，，，‎ ；‎ 又，‎ ；……4分 ‎（Ⅱ）∵ 折前，‎ ‎∴ 折起，‎ ‎∴ 平面，‎ ‎∴ ； …………………8分 ‎（Ⅲ）设点到平面的距离为，则由得，‎ ，解得．‎ ‎∴ 点到平面的距离为． …………………12分