高考数学专题复习：《函数与方程》同步训练题

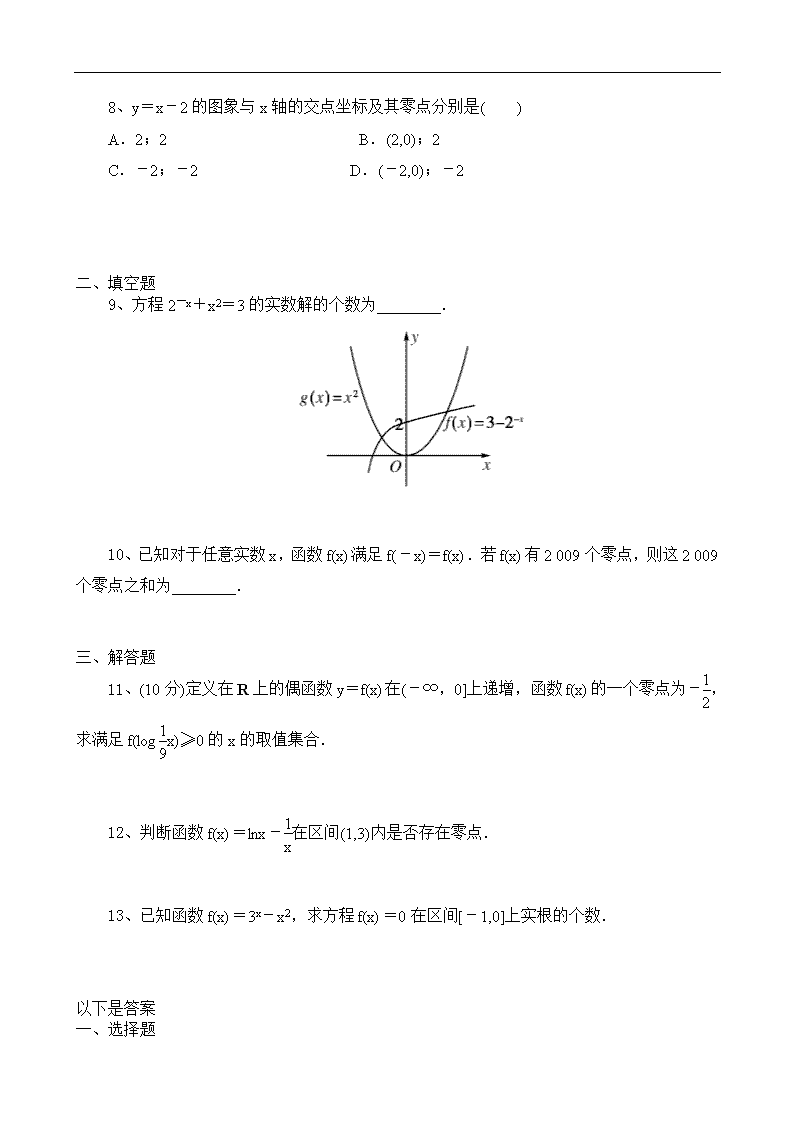
高考数学专题复习：《函数与方程》同步训练题

‎《函数与方程》同步训练题 一、选择题 ‎1、若函数f(x)的零点与g(x)＝4x＋2x－2的零点之差的绝对值不超过0.25，则f(x)可以是(　　)‎ A．f(x)＝4x－1 B．f(x)＝(x－1)2‎ C．f(x)＝ex－1 D．f(x)＝ln ‎2、设函数f(x)＝x3－x－2的零点为x0，则x0所在的区间是(　　)‎ A．(0,1) B．(1,2)‎ C．(2,3) D．(3,4)‎ ‎3、函数f(x)＝ax2＋2ax＋c(a≠0)的一个零点是－3，则它的另一个零点是(　　)‎ A．－1 B．1‎ C．－2 D．2‎ ‎4、函数f(x)＝x2＋x＋3的零点的个数是(　　)‎ A．0 B．1‎ C．2 D．3‎ ‎5、函数f(x)＝x2－ax－b的两个零点是2和3，求函数g(x)＝bx2－ax－1的零点．‎ ‎6、函数f(x)＝x2－4x－5的零点是________．‎ ‎7、函数f(x)＝x2＋4x＋a没有零点，则实数a的取值范围是(　　)‎ A．a<4 B．a>4‎ C．a≤4 D．a≥4‎ ‎8、y＝x－2的图象与x轴的交点坐标及其零点分别是(　　)‎ A．2；2 B．(2,0)；2‎ C．－2；－2 D．(－2,0)；－2‎ 二、填空题 ‎9、方程2－x＋x2＝3的实数解的个数为________．‎ ‎10、已知对于任意实数x，函数f(x)满足f(－x)＝f(x)．若f(x)有2 009个零点，则这2 009个零点之和为________．‎ 三、解答题 ‎11、(10分)定义在R上的偶函数y＝f(x)在(－∞，0]上递增，函数f(x)的一个零点为－，求满足f(logx)≥0的x的取值集合．‎ ‎12、判断函数f(x)＝lnx－在区间(1,3)内是否存在零点．‎ ‎13、已知函数f(x)＝3x－x2，求方程f(x)＝0在区间[－1,0]上实根的个数．‎ 以下是答案 一、选择题 ‎1、【解析】　4个选项中的零点是确定的．‎ A：x＝；B：x＝1；C：x＝0；D：x＝.‎ 又∵g(0)＝40＋2×0－2＝－1<0，‎ g＝4＋2×－2＝1>0，‎ ‎∴g(x)＝4x＋2x－2的零点介于之间．从而选A.‎ ‎【答案】　A ‎2、【解析】　解法一：令f(x)＝x3－()x－2，‎ 则f(0)＝0－()－2＝－4<0，‎ f(1)＝1－()－2＝－1<0，‎ f(2)＝23－()0＝7>0，‎ f(3)＝27－()1＝26>0，‎ f(4)＝43－()2＝63>0，‎ ‎∴f(1)·f(2)<0，‎ 故x0所在的区间是(1,2)．‎ 解法二：数形结合法，如图所示．‎ ‎【答案】　B ‎3、【解析】　由根与系数的关系得 ‎－3＋x＝－，∴x＝1.‎ 即另一个零点是1，故选B.‎ ‎【答案】　B ‎4、【解析】　方程x2＋x＋3＝0中，判别式Δ＝－11<0，故方程无实根，函数没有零点．‎ ‎【答案】　A ‎5、【解析】　由题意知方程x2－ax－b＝0的两根分别为2和3，‎ ‎∴a＝5，b＝－6，‎ ‎∴g(x)＝－6x2－5x－1.‎ 由－6x2－5x－1＝0得 x1＝－，x2＝－.‎ ‎∴函数g(x)的零点是－，－.‎ ‎6、　x2－4x－5＝(x－5)(x＋1)＝0，∴x＝5或－1.‎ ‎【答案】　－1或5‎ ‎7、B.　Δ＝16－‎4a<0，∴a>4.故选B ‎8、B【解析】　由y＝x－2＝0，得x＝2，‎ 故交点坐标为(2,0)，零点是2.‎ 二、填空题 ‎9、【解析】　分别作出函数f(x)=3-2-x与函数g(x)=x2的图象，如图所示．‎ ‎∵f(0)=2，g(0)=0，∴从图象上可以看出它们有2个交点．‎ ‎【答案】　2‎ ‎10、【解析】　设x0为其中一根，即f(x0)＝0，因为函数f(x)满足f(－x)＝f(x)，所以f(－x0)＝f(x0)＝0，‎ 即－x0也为方程一根，又因为方程f(x)＝0有2 009个实数解，所以其中必有一根x1，满足x1＝－x1，即x1＝0，所以这2 009个实数解之和为0.‎ ‎【答案】　0‎ 三、解答题 ‎11、【解析】　∵－是函数的一个零点，‎ ‎∴f(－)＝0.‎ ‎∵y＝f(x)是偶函数，且在(－∞，0]上递增，‎ ‎∴当logx≤0，即x≥1时，logx≥－，解得x≤3.即1≤x≤3.‎ 由对称性可知，当logx>0时，≤x<1.‎ 综上所述，x的取值范围为[，3].‎ ‎ ‎ ‎12、【解析】　因为函数f(x)＝ln x－的图象在[1,3]上是连续不断的一条曲线，且f(1)＝－1<0，f(3)＝ln 3－>0，从而由零点存在性定理知，函数在(1,3)内存在零点．‎ ‎13、【解析】　∵f(－1)＝3－1－(－1)2＝－<0，‎ f(0)＝30－02＝1>0，‎ ‎∴f(－1)·f(0)<0.‎ 又函数f(x)在[－1,0]上的图象是连续曲线，‎ ‎∴方程f(x)＝0在[－1,0]内有实根．‎ 又函数f(x)＝3x－x2在[－1,0]上是增函数，‎ ‎∴方程f(x)＝0在[－1,0]上只有一个实数根．‎