高一数学（人教A版）必修4能力提升：1-4-3 正切函数的性质与图象

高一数学（人教A版）必修4能力提升：1-4-3 正切函数的性质与图象

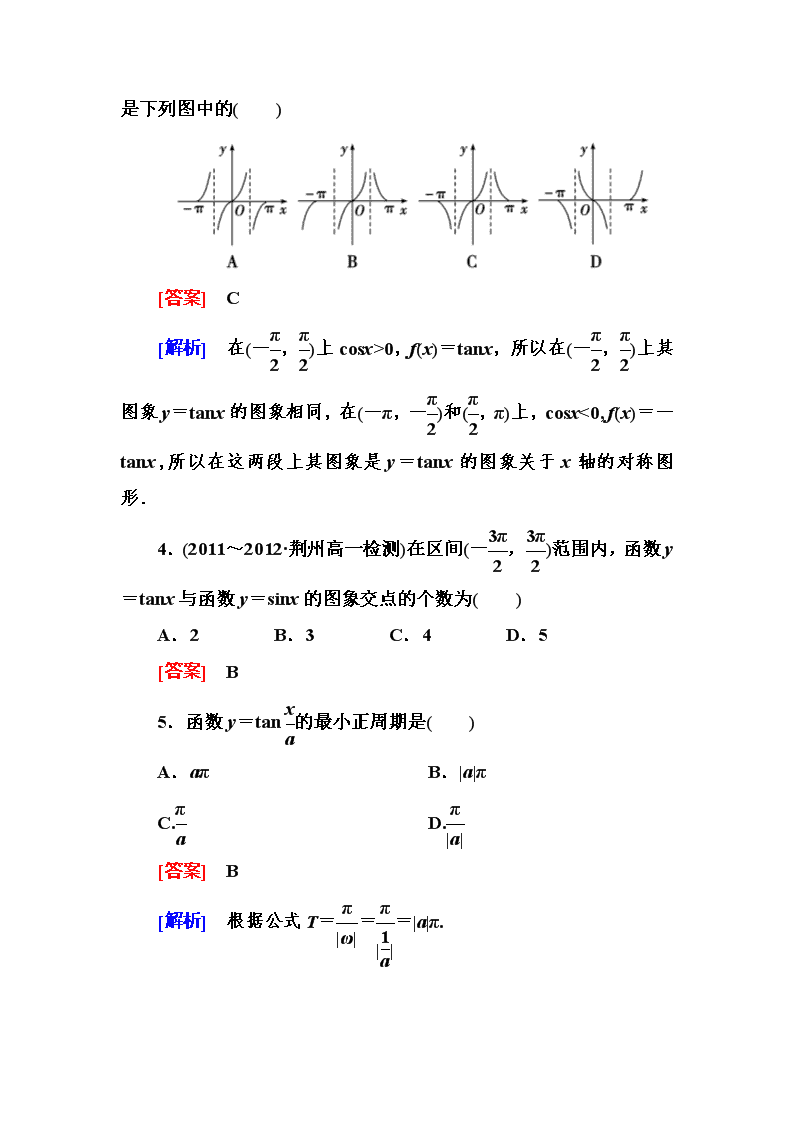
能 力 提 升 一、选择题 1．函数 y＝3tan 2x＋π 4 的定义域是( ) A. x|x≠kπ＋π 2 ，k∈Z B. x|x≠k 2π－3π 8 ，k∈Z C. x|x≠k 2π＋π 8 ，k∈Z D. x|x≠k 2π，k∈Z [答案] C [解析] 要使函数有意义，则 2x＋π 4 ≠kπ＋π 2(k∈Z)，则 x≠k 2π＋ π 8(k∈Z)． 2．函数 y＝tanx＋ 1 tanx 是( ) A．奇函数 B．偶函数 C．既是奇函数又是偶函数 D．既不是奇函数又不是偶函数 [答案] A [解析] 定义域是 x|x≠kπ＋π 2 ，k∈Z ∩{x|x≠kπ，k∈Z}＝ x|x≠kπ 2 ，k∈Z . 又 f(－x)＝tan(－x)＋ 1 tan－x ＝－ tanx＋ 1 tanx ＝－f(x)，即函数 y＝tanx＋ 1 tanx 是奇函数． 3．(福建福州模拟)函数 f(x)＝ sinx |cosx| 在区间[－π，π]内的大致图象 是下列图中的( ) [答案] C [解析] 在(－π 2 ，π 2)上 cosx>0，f(x)＝tanx，所以在(－π 2 ，π 2)上其 图象 y＝tanx 的图象相同，在(－π，－π 2)和(π 2 ，π)上，cosx<0, f(x)＝ －tanx，所以在这两段上其图象是 y＝tanx 的图象关于 x 轴的对称图 形． 4．(2011～2012·荆州高一检测)在区间(－3π 2 ，3π 2 )范围内，函数 y ＝tanx 与函数 y＝sinx 的图象交点的个数为( ) A．2 B．3 C．4 D．5 [答案] B 5．函数 y＝tan x a 的最小正周期是( ) A．aπ B．|a|π C.π a D. π |a| [答案] B [解析] 根据公式 T＝ π |ω| ＝ π |1 a| ＝|a|π. 6．下列函数中，同时满足：①在(0，π 2)上是增函数，②为奇函 数，③以π为最小正周期的函数是( ) A．y＝tanx B．y＝cosx C．y＝tanx 2 D．y＝|sinx| [答案] A [解析] 经验证，选项 B、D 中所给函数都是偶函数，不符合； 选项 C 中所给的函数的周期为 2π. 二、填空题 7．函数 y＝3tan(2x＋π 3)的对称中心的坐标为________________． [答案] (kπ 4 －π 6 ，0)(k∈Z) [解析] 令 2x＋π 3 ＝kπ 2 (k∈Z)， 得 x＝kπ 4 －π 6(k∈Z)， ∴对称中心的坐标为(kπ 4 －π 6 ，0)(k∈Z)． 8．(辽宁沈阳实中模拟)求函数 y＝tan(－1 2x＋π 4)的单调区间是 ________________． [答案] (2kπ－π 2 ，2kπ＋3 2π)(k∈Z) [解析] y＝tan(－1 2x＋π 4) ＝－tan(1 2x－π 4)， 由 kπ－π 2<1 2x－π 41，即 a>2 时，二次函 数在[－1,1]上递减，ymin＝(1－a 2)2－a2 4 ＝1－a＝－6，∴a＝7. 综上所述，a＝7 或 a＝－7. 11．已知函数 f(x)＝tanωx(ω>0)的图象的相邻两支截直线 y＝π 4 所 得线段长为π 4 ，求 f(π 4)的值． [解析] ∵ω>0，∴函数 f(x)＝tanωx 的周期为π ω ， 且在每个独立区间内都是单调函数， ∴两交点之间的距离为π ω ＝π 4 ， ∴ω＝4，f(x)＝tan4x， ∴f(π 4)＝tanπ＝0. 12．已知函数 f(x)＝3tan(1 2x－π 3)． (1)求 f(x)的定义域、值域； (2)讨论 f(x)的周期性，奇偶性和单调性． [解析] (1)由 1 2x－π 3 ≠π 2 ＋kπ，k∈Z， 解得 x≠5π 3 ＋2kπ，k∈Z. ∴定义域为{x|x≠5π 3 ＋2kπ，k∈Z}，值域为 R. (2)f(x)为周期函数，周期 T＝π 1 2 ＝2π. f(x)为非奇非偶函数． 由－π 2 ＋kπ<1 2x－π 3<π 2 ＋kπ，k∈Z， 解得－π 3 ＋2kπ

查看更多