江苏省无锡市大桥实验学校2019-2020学年高一下学期期中考试数学试题

江苏省无锡市大桥实验学校2019-2020学年高一下学期期中考试数学试题

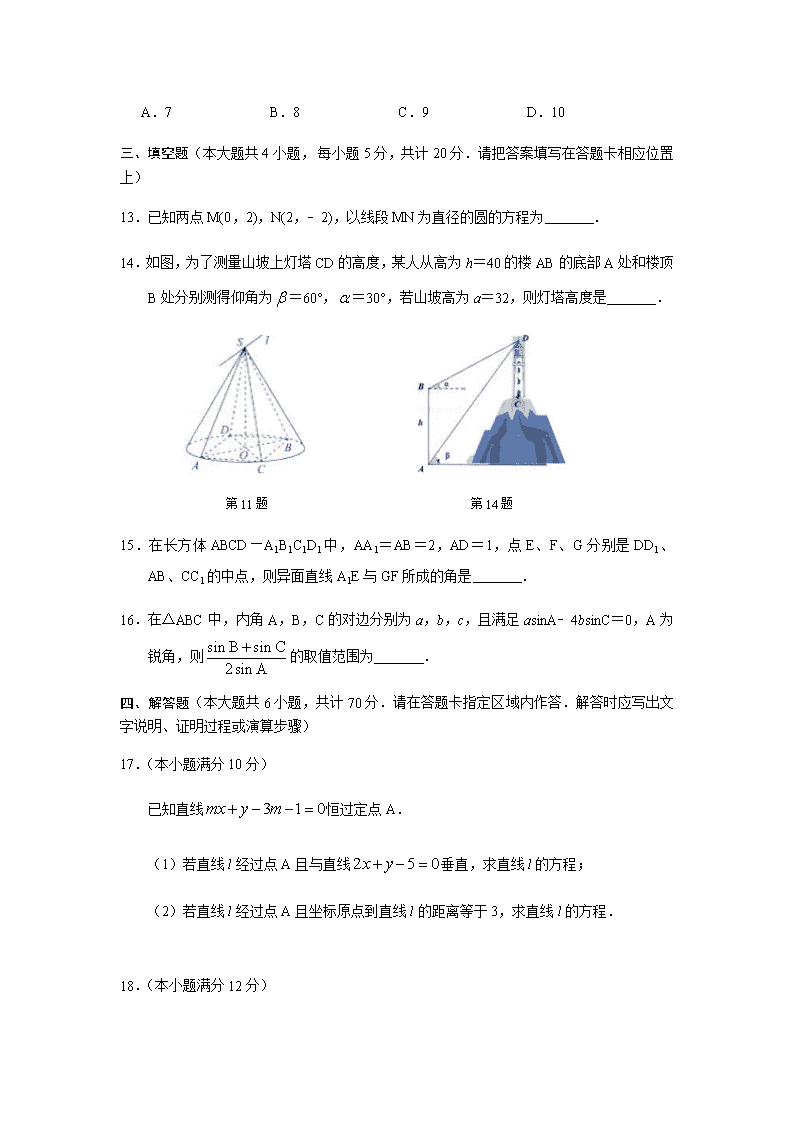
无锡市大桥实验学校2019—2020学年度第二学期期中考试 高一数学试卷 ‎2020．5‎ 一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎1．直线的倾斜角是 ‎ A．30° B．60° C．120° D．150°‎ ‎2．已知m为实数，直线l1：，l2：，若l1∥l2，则实数m的值 ‎ A．2 B．1 C．1或2 D．0或 ‎3．过点A(1，﹣1)、B(﹣1，1)且圆心在直线上的圆的方程是 ‎ A． B．‎ ‎ C． D．‎ ‎4．在△ABC，已知acosA＝bcosB，则△ABC的形状是 A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰三角形或直角三角形 ‎5．设m，n是两条不同的直线，，是两个不同的平面，则下列命题正确的是 A．若m∥n，n∥，则m∥n B．若∥，m，n，则m∥n C．若⊥＝m，n，则n⊥ D．若m⊥，m∥n，n，则⊥‎ ‎6．已知直线与圆C：交于A，B两点，则弦AB的长为 ‎ A．1 B． C．2 D．‎ ‎7．在△ABC中，角A，B，C的对边分别是a，b，c，若a：b：c＝4：3：2，则 ＝‎ ‎ A． B． C． D．‎ ‎8．已知某三棱柱的侧棱垂直于底面，且底面是边长为2的正三角形，若其外接球的表面积为，则该三棱柱的高为 ‎ A． B．3 C．4 D．‎ 二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎9．在△ABC中角A，B，C所对的边分别是a，b，c，若A＝，，，则角C大小是 ‎ A． B． C． D．‎ ‎10．若直线过点A(1，2)，且在两坐标轴上截距的绝对值相等，则直线l方程可能为 A． B． C． D．‎ ‎11．如图，已知圆锥的顶点为S，底面圆O的两条直径分别为AB和CD，且AB⊥CD，若平面SAD平面SBC＝l．以下四个结论中正确的是 A．AD∥平面SBC B．l∥AD C．若E是底面圆周上的动点，则△SAE的最大面积等于△SAB的面积 D．l与平面SCD所成的角为45°‎ ‎12．P，Q分别为圆M：与圆N：上的动点，A为x轴上的动点，则的值可能是 ‎ A．7 B．8 C．9 D．10‎ 三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）‎ ‎13．已知两点M(0，2)，N(2，﹣2)，以线段MN为直径的圆的方程为 ．‎ ‎14．如图，为了测量山坡上灯塔CD的高度，某人从高为h＝40的楼AB的底部A处和楼顶 B处分别测得仰角为＝60°，＝30°，若山坡高为a＝32，则灯塔高度是 ．‎ ‎ ‎ ‎ 第11题 第14题 ‎15．在长方体ABCD—A1B1C1D1中，AA1＝AB＝2，AD＝1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是 ．‎ ‎16．在△ABC中，内角A，B，C的对边分别为a，b，c，且满足asinA﹣4bsinC＝0，A为锐角，则的取值范围为 ．‎ 四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）‎ 已知直线恒过定点A．‎ ‎（1）若直线l经过点A且与直线垂直，求直线l的方程；‎ ‎（2）若直线l经过点A且坐标原点到直线l的距离等于3，求直线l的方程．‎ ‎18．（本小题满分12分）‎ 如图，已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点，AB是直径，CD＝1，直线CD⊥平面ABC．‎ ‎（1）证明：AC⊥BD；‎ ‎（2）若M为BD的中点，求证：OM∥平面DAC；‎ ‎（3）求三棱锥D—ABC的体积．‎ ‎19．（本小题满分12分）‎ 设△ABC的内角A，B，C的对边分别为a，b，c，已知2bcosB＝acosC＋ccosA．‎ ‎（1）求B；‎ ‎（2）若b＝，求a＋c的取值范围．‎ ‎20．（本小题满分12分）‎ 如图，在多面体ABCDEF中，ABCD是正方形，BF⊥平面ABCD，DE⊥平面ABCD，BF＝DE，点M为棱AE的中点．‎ ‎（1）求证：BD//EF；‎ ‎（2）求证：平面BMD∥平面EFC；‎ ‎（3）若AB＝1，BF＝2，求E点到平面ACF的距离．‎ ‎21．（本小题满分12分）‎ 如图，在某商业区周边有两条公路l1和l2，在点O处交汇；该商业区为圆心角、半径3km 的扇形．现规划在该商业区外修建一条公路AB，与l1，l2分别交于A，B，要求AB与扇形弧相切，切点T不在l1，l2上．‎ ‎（1）设OA＝akm，OB＝bkm 试用a，b表示新建公路AB的长度，求出a，b满足的关系式，并写出a，b的范围；‎ ‎（2）设∠AOT＝，试用表示新建公路AB的长度，并且确定A，B的位置，使得新建公路AB的长度最短．‎ ‎22．（本小题满分12分）‎ 如图，圆C与x轴相切于点T(1，0)，与y轴正半轴交于两点A，B（B在A的上方），且＝2．‎ ‎（1）求圆C的标准方程；‎ ‎（2）过点A任作一条直线与圆O：相交于M，N两点．①求证：为定值，并求出这个定值；②求△BMN的面积最大值．‎ 参考答案 ‎1．D 2．B 3．C 4．D 5．D 6．C 7．D 8．B ‎9．BD 10．ABC 11．ABD 12．CD ‎13． 14．28 15． 16．(，)‎ ‎17．‎ ‎ ‎ ‎18．‎ ‎19．‎ ‎ ‎ ‎20．‎ ‎21．‎ ‎ ‎ ‎ ‎ ‎22．‎