- 2021-06-23 发布 |
- 37.5 KB |
- 9页
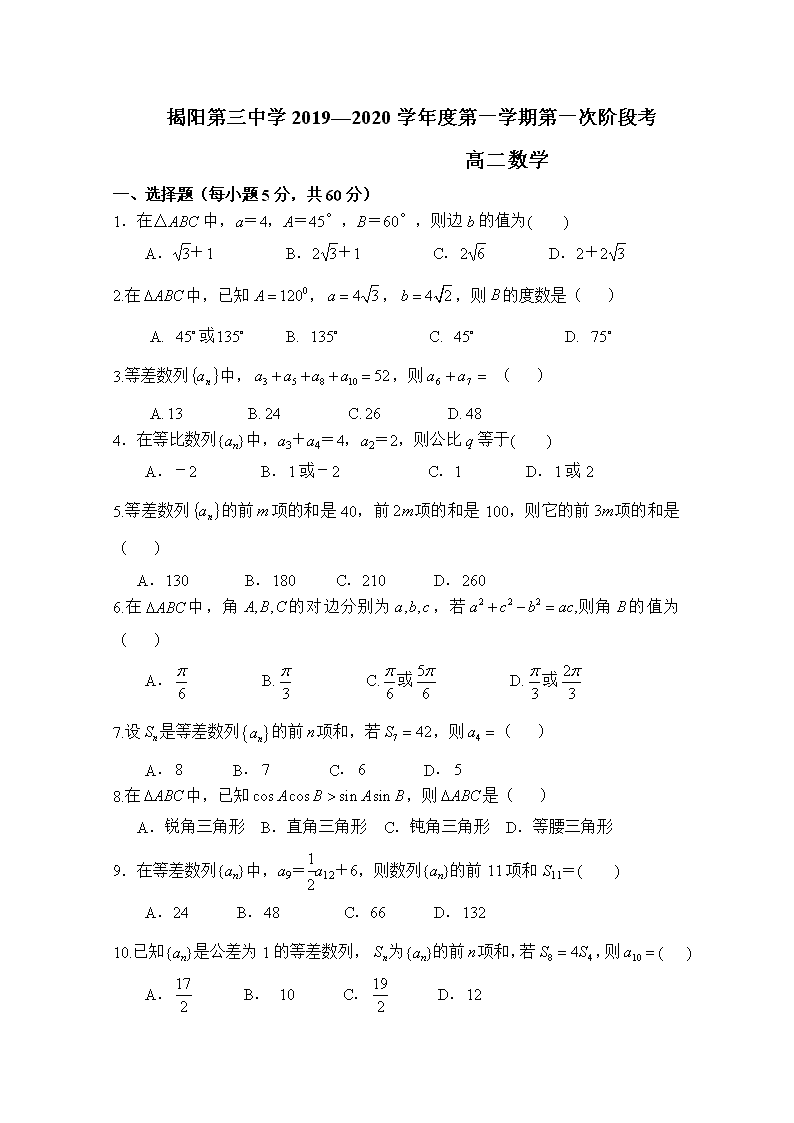


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年广东省揭阳市第三中学高二上学期第一次月考数学试题 word版
揭阳第三中学2019—2020学年度第一学期第一次阶段考 高二数学 一、选择题(每小题5分,共60分) 1.在△ABC中,a=4,A=45°,B=60°,则边b的值为( ) A.+1 B.2+1 C.2 D.2+2 2.在中,已知,,,则的度数是( ) A. 或 B. C. D. 3.等差数列中,,则 ( ) A. B. C. D. 4.在等比数列{an}中,a3+a4=4,a2=2,则公比q等于( ) A.-2 B.1或-2 C.1 D.1或2 5.等差数列的前项的和是40,前项的和是100,则它的前项的和是( ) A.130 B.180 C.210 D.260 6.在中,角的对边分别为,若则角的值为 ( ) A. B. C.或 D.或 7.设是等差数列的前项和,若,则( ) A. B. C. D. 8.在中,已知,则是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 9.在等差数列{an}中,a9=a12+6,则数列{an}的前11项和S11=( ) A.24 B.48 C.66 D.132 10.已知{an}是公差为1的等差数列,为{an}的前项和,若,则( ) A. B. 10 C. D.12 11.已知数列满足,若,则为 ( ) A. B. C. D. 12.设△ABC中角、、所对的边分别为,且,若成等差数列且,则边长为( ) A.5 B.6 C.7 D .8 二、填空题(每小题5分,共20分) 13.在△ABC中,ab=60,S△ABC=15,△ABC的外接圆半径为,则边c的长为________. 14.在中,则的值为________. 15.一船以每小时的速度向东航行,船在处看到一个灯塔在北偏东,行驶后,船到达C处,看到这个灯塔在北偏东,这时船与灯塔的距离为 . 16.数列{}的前项和为,若 . 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。) 17. (本小题满分10分) 在△ABC中,内角,,的对边分别为,,,且。 (1)求角的大小; (2)若,,求,的值. 18.(本小题满分12分) 设为等差数列,是等差数列的前项和,已知 ,. (1)求数列的通项公式; (2)为数列的前项和,求. 19. (本小题满分12分) 已知、、为的三内角,且其对边分别为、、,若. (1)求; (2)若,求的面积. A B C m l 20. (本小题满分12分) 如图,某河段的两岸可视为平行线 .有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距米的、两点,并观察对岸的点,测得,.() (1)求线段的长度; (2)求该河段的宽度. 21.(本小题满分12分)如果数列的前项和为. (1)求数列的通项公式; (2)求的最小值. 22.(本小题满分12分) 已知数列中,,,数列满足; (1)求证:数列是等差数列; (2)求数列中的最大值和最小值,并说明理由. 揭阳第三中学2019—2020学年第一学期第一次阶段答案 高二数学 一、选择题 1 2 3 4 5 6 7 8 9 10 11 12 C C C B B B C C D C D B 二、填空题 13. 3 14. 15. 16. 三、解答题 17. (本小题满分10分) 在△ABC中,内角,,的对边分别为,,,且。 (1)求角的大小; (2)若,,求,的值. 解:(1)∵,由正弦定理可得, ……2分 即得,……3分 ∴. ……5分 (2) ,由正弦定理得, ……6分 由余弦定理,得, ……8分 解得, ……9分 . ……10分 18.(本小题满分12分) 设为等差数列,是等差数列的前项和,已知,. (1)求数列的通项公式; (2)为数列的前项和,求. 解:(1)设等差数列的公差为, ……1分 则 ①,又 ② ……3分 联立①②,解得,,……5分 ∴数列的通项公式. ……6分 (2) ∵,∴, ……7分 ∴,……8分 又, ……9分 ∴数列为首项是-2,公差是等差数列,……10分 ∴. ……12分 19. (本小题满分12分) 已知、、为的三内角,且其对边分别为、、,若. (1)求; (2)若,求的面积. 解:(Ⅰ) ……2分 又, ……4分 , ……6分 (Ⅱ)由余弦定理 得 即:, ……9分 ……10分 ∴ ……12分 A B C m l D 20. (本小题满分12分) 如图,某河段的两岸可视为平行线.有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距米的、两点,并观察对岸的点,测得,. (1)求线段的长度; (2)求该河段的宽度. 解:(1)∵, ∴ …… 2分 由正弦定理得: ∴(米) …… 6分 (2)如图过点B作垂直于对岸,垂足为D,则BD的长就是该河段的宽度. …… 7分 在中,∵, ∴= ……11分 ∴该河段的宽度为米 …… 12分 21.(本小题满分12分)如果数列的前项和为. (1)求数列的通项公式; (2)求的最小值. 解:(1)当时, ……2分 当时,, ……5分 经检验,满足此式 ……6分 ∴ …… 7分 (2) ∵,…… 10分 ∴当时,取得最小值-576. ……12分 22.(本小题满分12分) 已知数列中,,,数列满足; (1)求证:数列是等差数列; (2)求数列中的最大值和最小值,并说明理由. (1)证明:∵ ……3分 又 ∴数列是首项为,公差为1的等差数列。……5分 (2) 解:由(1)可得: , ……7分 ∴ , ……9分 ∴当时,数列单调递减且,当时,数列单调递减且,……10分 ∴数列的最大值为,最小值为。……12分查看更多