2018-2019学年福建省武平县第一中学高二下学期期中考试 数学（文）Word版

2018-2019学年福建省武平县第一中学高二下学期期中考试 数学（文）Word版

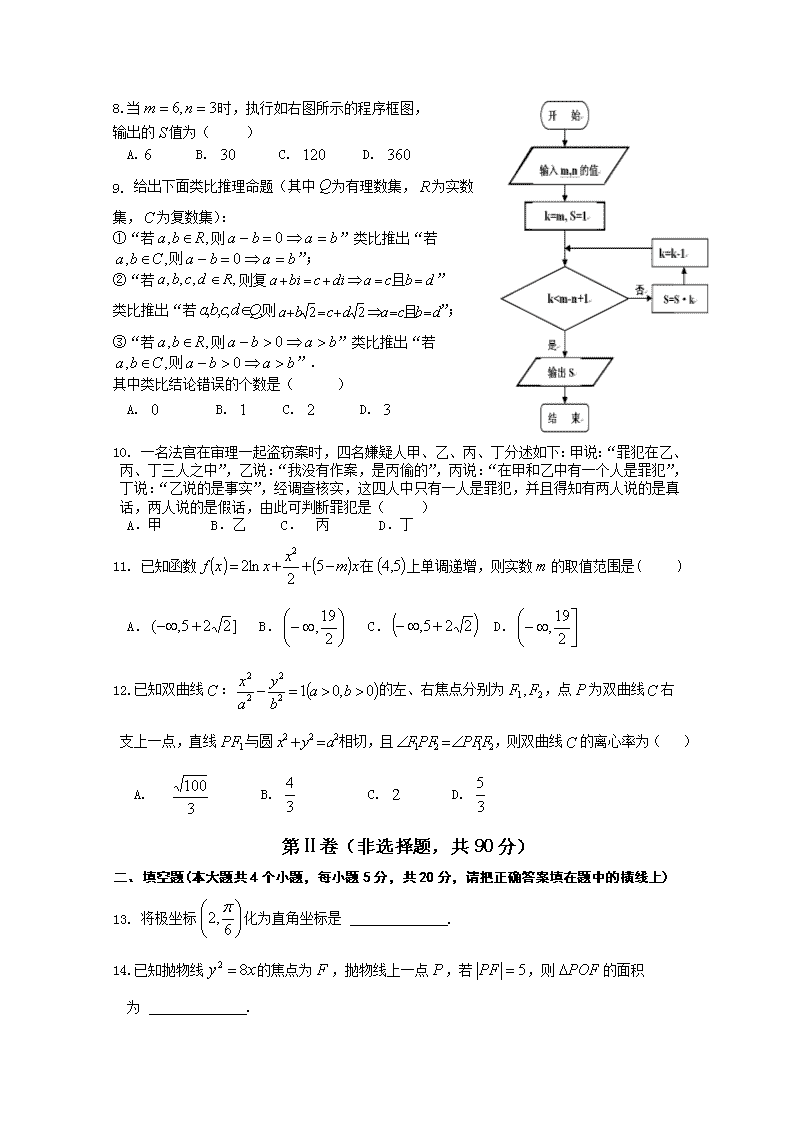
武平一中2018-2019学年第二学期半期考 高二数学(文)试题 ‎（考试时间：120分钟 总分：150分）‎ ‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.若为虚数单位，则复数的共轭复数是（　 ）‎ A. 　　 B. 　　 C. 　 D. ‎ ‎2. 设,则“”是“”的（ 　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎3.矩形的对角线互相垂直，正方形是矩形，所以正方形的对角线互相垂直。在以上三段论的推理中（ ）‎ A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 结论错误 ‎4.若洗水壶要用 分钟、烧开水要用分钟、洗茶杯要用分钟、取茶叶要用分钟、 沏茶 分钟，那么较合理的安排至少也需要 （ ）‎ A. 分钟 B. 分钟 C. 分钟 D. 分钟 ‎5. 用反证法证明命题:“若且，则全为”时，应假设为（　 　）‎ A.且 B.不全为 C.中至少有一个为 D.中只有一个为 ‎6.若，，则的大小关系是（ ）‎ A. B. C. D. 的大小由的取值确定 ‎7.下列有关命题的说法正确的是（ ）‎ A.若为真命题，则均为真命题. ‎ B.命题“若，则”的逆否命题为假命题.‎ C.命题：，则￢为：.‎ D.命题“若则或”的否命题为“若则或”.‎ ‎8.当时，执行如右图所示的程序框图，‎ 输出的值为（　 　）‎ A. B. C. D. ‎ 9. 给出下面类比推理命题（其中为有理数集，为实数集，为复数集）：‎ ‎①“若则”类比推出“若则”；‎ ‎②“若则复”‎ 类比推出“若则”；‎ ‎③“若则”类比推出“若则”. ‎ 其中类比结论错误的个数是（　 　）‎ A. 　 B. 　 C. 　 D. ‎ 10. 一名法官在审理一起盗窃案时，四名嫌疑人甲、乙、丙、丁分述如下：甲说：“罪犯在乙、‎ 丙、丁三人之中”，乙说：“我没有作案，是丙偷的”，丙说：“在甲和乙中有一个人是罪犯”，丁说：“乙说的是事实”，经调查核实，这四人中只有一人是罪犯，并且得知有两人说的是真话，两人说的是假话，由此可判断罪犯是（ ）‎ A．甲 B．乙 C． 丙 D．丁 ‎11. 已知函数在上单调递增，则实数的取值范围是(　 )‎ A． B． C． D．‎ ‎12.已知双曲线：的左、右焦点分别为，点为双曲线右支上一点，直线与圆相切，且，则双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎　　　　　　　　　　　　第Ⅱ卷（非选择题，共90分）‎ 二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中的横线上)‎ ‎13. 将极坐标化为直角坐标是 . ‎ ‎14.已知抛物线的焦点为，抛物线上一点，若，则的面积 为 . ‎ ‎15.已知命题：存在，使得成立，命题对任意， 恒成立，若命题是真命题，则实数的取值范围是 . ‎ ‎16.传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数．他们研究过如图所示的三角形数：‎ 将三角形数记为数列，将可被整除的三角形数按从小到大的顺序组成一个新数列，可以推测：是数列中的第 项． ‎ 三、解答题(本大题共6小题，共70分．解答应写出文字说明, 证明过程或演算步骤.)‎ ‎17.（本题满分10分）已知函数，其中为实数，且在处取得的极值为。‎ ‎⑴求的表达式；‎ ‎⑵若在处的切线方程。‎ ‎18.（本题满分12分）为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查．已知该校共有学生人，其中男生人，从全校学生中抽取了容量为的样本，得到一周参加社区服务的时间的统计数据好下表：‎ 超过小时 不超过小时 男 女 ‎（1）求；‎ ‎（2）能否有%的把握认为该校学生一周参加社区服务时间是否超过小时与性别有关？‎ 附：‎ ‎19.（本题满分12分）“双十一网购狂欢节”源于淘宝商城（天猫）年月日举办的促销活动，当时参与的商家数量和促销力度均有限，但营业额远超预想的效果，于是月日成为天猫举办大规模促销活动的固定日期.如今，中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近年“双十一”期间的宣传费用（单位：万元）和利润（单位：十万元）之间的关系，搜集了相关数据，得到下列表格：‎ ‎（万元）‎ ‎（十万元）‎ ‎（1）请用相关系数说明与之间是否存在线性相关关系（当时，说明与 之间具有线性相关关系）；‎ ‎（2）建立关于的线性回归方程（系数精确到），预测当宣传费用为万元时的利润，‎ 附参考公式：回归方程中和最小二乘估计公式分别为 ‎，，相关系数 参考数据：，，，‎ ‎20．（本题满分12分）在平面直角坐标系中，已知曲线（为参数），在以原点为极点， 轴的非负半轴为极轴建立的极坐标系中，直线的极坐标方程为．‎ ‎（1）求曲线的普通方程和直线的直角坐标方程；‎ ‎（2）过点且与直线平行的直线交于两点，求线段的距离．‎ ‎21.（本题满分12分）已知，动点满足,设动点的轨迹为曲线．‎ ‎（1）求曲线的方程；‎ ‎（2）已知直线与曲线交于两点，若点，求证：为定值.‎ ‎22.（本题满分12分）已知函数.‎ ‎（1）讨论的单调性；‎ ‎（2）当时，不等式对于任意恒成立，求实数的取值范围.‎ 参考答案 一、选择题(本大题共12小题，每小题5分，共60分．)‎ ‎　　CAACB ACCBB DD 二、填空题(本大题共4个小题，每小题5分，共20分)‎ ‎13. 14.　　　15. 　　　　　16.‎ 三、解答题(本大题共6小题，共70分．解答应写出文字说明, 证明过程或演算步骤.)‎ ‎17.【解】(1)因为，所以; ........1分 由在处取得的极值为，可得，..........3分 解之得：,经检验，符合题意 ‎ 所以（没检验扣1分）. ...........6分 ‎(2)由(1)可得，，，‎ 所以切线方程为. 　　　　　　　　　..........10分 ‎18. 【解】（1）由已知，该校有女生400人，故，得　　，.....3分 从而． 　　..........5分 ‎（2）作出列联表如下：‎ 超过小时的人数 不超过小时的人数 合计 男 女 合计 ‎． 　　 ...........11分 所以没有%的把握认为该校学生一周参加社区服务时间是否超过小时与性别有关．‎ ‎...........12分 ‎19. 解：（1）由题意得， ...........2分 又，，，‎ 所以 ...........4分 所以，与之间具有线性相关关系. ...........5分 ‎（2）因为， 　　　 　..........7分 ‎（或，）‎ ‎...........9分 所以关于的线性回归方程为 .‎ 当时，‎ 故可预测当宣传费用为万元时的利润为十万元（或万元）　　.......12分 ‎20．解：（1）曲线化为普通方程为， .　　　　..........3分 由，得，‎ 所以直线的直角坐标方程为． 　　　　　　　 ...........6分 （2） 直线的参数方程为（为参数），‎ 代入,化简得， ‎ 设两点所对应的参数分别为， ，‎ 则，∴　　　　　．...........12分 ‎21.解：设动点，，动点M满足 ，‎ 可得：，得曲线C的方程：　.......5分 ‎(注:没写扣1分)‎ · 由，得，显然.‎ 设，由韦达定理得：，‎ ‎...........7分 ‎ ‎ 为定值． 　　　　　　　...........12分 22. 解：（1）函数的定义域为， ...........1分 当时，，所以在上单调递增； 　 ...........2分 当时，令得，；令得，.‎ 则函数在上单调递增，在上单调递减.‎ 综上所述，当时，在上单调递增；‎ 当时，在上单调递增，在上单调递减.‎ ‎ 　　　 ...........5分 ‎ ‎（2）设，‎ 则题意等价于：当时，恒成立，只需.‎ ‎，设，则，‎ 所以在上单调递增.又，，‎ 所以存在唯一，使，即，‎ 且当时，，即，函数单调递减，‎ 当时，，即，函数单调递增.‎ 所以，‎ 即.‎ 所以，实数的取值范围为. 　　　　 ...........12分