【数学】2019届一轮复习人教A版平面向量的概念及其线性运算学案

【数学】2019届一轮复习人教A版平面向量的概念及其线性运算学案

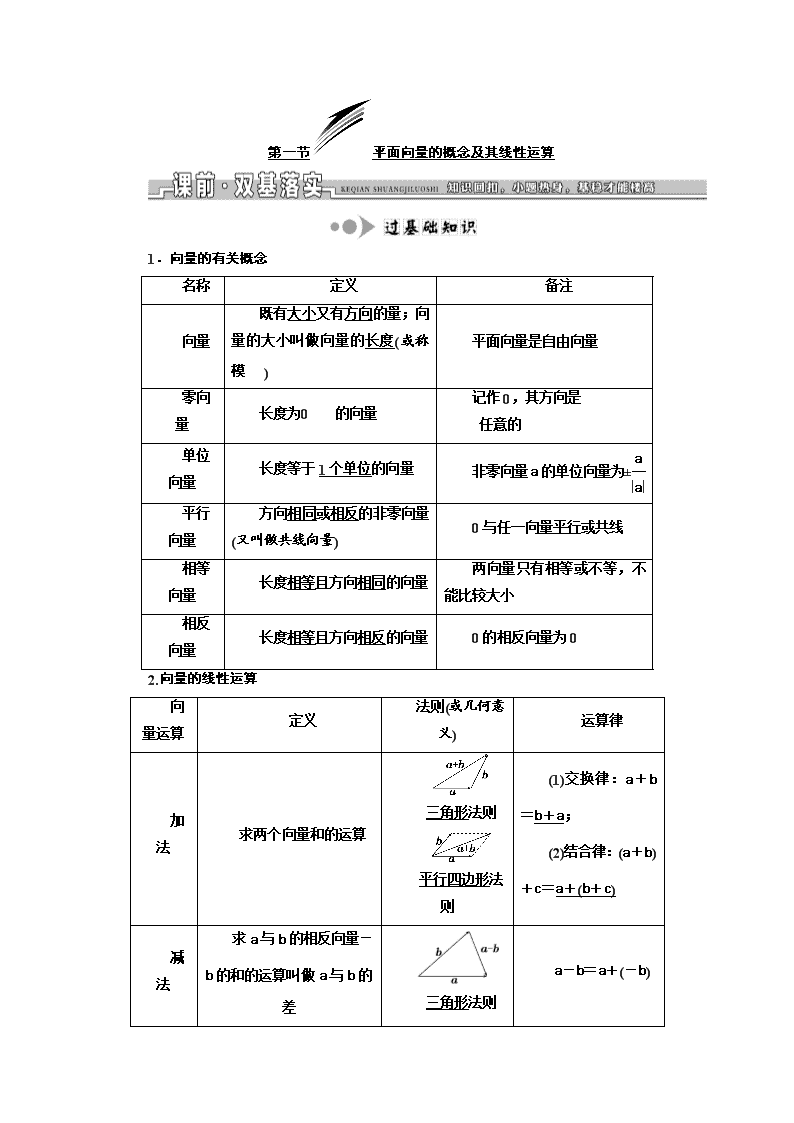
第一节平面向量的概念及其线性运算 ‎1．向量的有关概念 名称 定义 备注 向量 既有大小又有方向的量；向量的大小叫做向量的长度(或称)‎ 平面向量是自由向量 零向量 长度为的向量 记作0，其方向是 ‎ 任意的 单位向量 长度等于1个单位的向量 非零向量a的单位向量为± 平行向量 方向相同或相反的非零向量(又叫做共线向量)‎ ‎0与任一向量平行或共线 相等向量 长度相等且方向相同的向量 两向量只有相等或不等，不能比较大小 相反向量 长度相等且方向相反的向量 ‎0的相反向量为0‎ ‎2.向量的线性运算 向量运算 定义 法则(或几何意义)‎ 运算律 加法 求两个向量和的运算 三角形法则 平行四边形法则 ‎(1)交换律：a＋b＝b＋a；‎ ‎(2)结合律：(a＋b)＋c＝a＋(b＋c)‎ 减法 求a与b的相反向量－b的和的运算叫做a与b的差 三角形法则 a－b＝a＋(－b)‎ 数乘 求实数λ与向量a的积的运算 ‎（1）|λa|＝|λ||a|；‎ ‎（2）当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ＝0时，λa＝0‎ λ(μa)＝(λμ)a；‎ ‎(λ＋μ)a＝λa＋μa；‎ λ(a＋b)＝λa＋λb ‎3.共线向量定理 向量a(a≠0)与b共线，当且仅当有唯一一个实数λ，使得b＝λa.‎ ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．(　　)‎ ‎(2)|a|与|b|是否相等与a，b的方向无关．(　　)‎ ‎(3)若向量与向量是共线向量，则A，B，C，D四点在一条直线上．(　　)‎ ‎(4)当两个非零向量a，b共线时，一定有b＝λa，反之成立．(　　)‎ 答案：(1)×　(2)√　(3)×　(4)√‎ ‎2.如图，设P，Q两点把线段AB三等分，则下列向量表达式错误的是(　　)‎ A．＝　　　　　　 B．＝ C．＝－ D．＝ 解析：选D　由数乘向量的定义可以得到A、B、C都是正确的，只有D错误．‎ ‎3．设a，b都是非零向量，下列四个选项中，一定能使＋＝0成立的是(　　)‎ A．a＝2b B．a∥b C．a＝－b D．a⊥b 解析：选C　“＋＝0，且a，b都是非零向量”等价于“非零向量a，b共线且反向”，故答案为C.‎ ‎4．设D为△ABC所在平面内一点，＝3，则(　　)‎ A．＝－＋ B．＝－ C．＝＋ D．＝－ 解析：选A　由题意得＝＋＝＋＝＋－＝－＋.‎ ‎5．若菱形ABCD的边长为2，则|－＋|＝________.‎ 解析：|－＋c|＝|＋＋|＝||＝2.‎ 答案：2‎ ‎6．已知a与b是两个不共线向量，且向量a＋λb与－(b－‎3a)共线，则λ＝________.‎ 解析：由题意知存在k∈R，使得a＋λb＝k[－(b－‎3a)]，所以解得 答案：－ 　　　　 ‎[考什么·怎么考]‎ 高考对本部分内容不会单独考查，多渗透到平面向量的线性运算中，难度较小.‎ ‎1．设a0为单位向量，下列命题中：①若a为平面内的某个向量，则a＝|a|·a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0，假命题的个数是(　　)‎ A．0　　　　　　　　　 B．1‎ C．2 D．3‎ 解析：选D　向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．‎ 综上所述，假命题的个数是3.‎ ‎2．给出下列命题：‎ ‎①若a＝b，b＝c，则a＝c；‎ ‎②若A，B，C，D是不共线的四点，则＝是四边形ABCD为平行四边形的充要条件；‎ ‎③a＝b的充要条件是|a|＝|b|且a∥b；‎ ‎④若a∥b，b∥c，则a∥c.‎ 其中正确命题的序号是________．‎ 解析：①正确．∵a＝b，∴a，b的长度相等且方向相同，‎ 又b＝c，∴b，c的长度相等且方向相同，‎ ‎∴a，c的长度相等且方向相同，故a＝c.‎ ‎②正确．∵＝，∴||＝||且∥，‎ 又A，B，C，D是不共线的四点，‎ ‎∴四边形ABCD为平行四边形；‎ 反之，若四边形ABCD为平行四边形，‎ 则∥且||＝||，因此，＝.‎ ‎③不正确．当a∥b且方向相反时，即使|a|＝|b|，也不能得到a＝b，故|a|＝|b|且a∥b不是a＝b的充要条件，而是必要不充分条件．‎ ‎④不正确．考虑b＝0这种特殊情况．‎ 综上所述，正确命题的序号是①②.‎ 答案：①②‎ ‎[怎样快解·准解]‎ 有关平面向量概念的6个注意点 ‎(1)相等向量具有传递性，非零向量的平行也具有传递性．‎ ‎(2)共线向量即为平行向量，它们均与起点无关．‎ ‎(3)向量可以平移，平移后的向量与原向量是相等向量．解题时，不要把它与函数图象的移动混淆．‎ ‎(4)非零向量a与的关系：是与a同方向的单位向量，－是与a反方向的单位向量．‎ ‎(5)两个向量不能比较大小，只可以判断它们是否相等，但它们的模可以比较大小．‎ ‎(6)两平行向量有向线段所在的直线平行或重合，易忽视重合这一条件．‎ 　　　　 ‎[考什么·怎么考]‎ 平面向量的线性运算是高考对平面向量考查的一个重点内容，主要考查三角形法则及平行四边形法则的应用，通常有两个考查角度：‎ ‎(1)向量的线性表示；‎ ‎(2)加(减)法运算几何意义的应用．‎ 考题多以选择题或填空题的形式出现，属于低档题目．‎ ‎1．(2018·武汉调研)设M为平行四边形ABCD对角线的交点，O为平行四边形ABCD所在平面内的任意一点，则＋＋＋等于(　　)‎ A． 　　　　　　　　　 B．2 C．3 D．4 解析：选D　因为M是平行四边形ABCD对角线AC，BD的交点，所以＋＝2，＋＝2，所以＋＋＋＝4.‎ ‎2．(2018·广东五校协作体第一次诊断考试)设D是△ABC所在平面内一点，＝2，则(　　)‎ A．＝－ B．＝－ C．＝－ D．＝－ 解析：选A　＝＋＝－＝－－＝－，选A.‎ ‎3．设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC.若＝λ1＋λ2 (λ1，λ2为实数)，则λ1＋λ2＝________.‎ 解析：＝＋＝＋＝＋(＋)＝－＋，所以λ1＝－，λ2＝，即λ1＋λ2＝.‎ 答案： ‎[怎样快解·准解]‎ ‎1．用已知向量表示未知向量的方法 构造三角形，关键在于搞清构成三角形的三个向量间的相互关系，能熟练地找出图形中的相等向量，熟练运用相反向量将加减法相互转化．‎ ‎2．用已知向量表示未知向量的4步骤 ‎(1)观察各向量的位置；‎ ‎(2)寻找相应的三角形或多边形；‎ ‎(3)运用法则找关系；‎ ‎(4)化简结果．‎ ‎3．向量线性运算的2个常用结论 ‎(1)在△ABC中，D是BC的中点，则＝(＋)；‎ ‎(2)O为△ABC的重心的充要条件是＋＋＝0.‎ 　　　　 向量共线问题常见题型有两种，一是根据条件证明三点共线，二是利用三点共线求参数的值.题目难度一般较小.‎ ‎[典题领悟]‎ 设两个非零向量a与b不共线，‎ ‎(1)若＝a＋b，＝‎2a＋8b，＝3(a－b)，‎ 求证：A，B，D三点共线；‎ ‎(2)试确定实数k，使ka＋b和a＋kb同向．‎ 解：(1)证明：∵＝a＋b，＝‎2a＋8b，＝‎3a－3b，‎ ‎∴＝＋＝‎2a＋8b＋‎3a－3b＝5(a＋b)＝5，‎ ‎∴，共线．又∵它们有公共点B，∴A，B，D三点共线．‎ ‎(2)∵ka＋b与a＋kb同向，‎ ‎∴存在实数λ(λ>0)，使ka＋b＝λ(a＋kb)，‎ 即ka＋b＝λa＋λkb.∴(k－λ)a＝(λk－1)b.‎ ‎∵a，b是不共线的两个非零向量，‎ ‎∴解得或 又∵λ>0，∴k＝1.‎ ‎[解题师说]‎ ‎1．共线向量定理的3个应用 证明向量共线 对于向量a，b，若存在实数λ，使a＝λb，则a与b共线 证明三点共线 若存在实数λ，使＝λ，则A，B，C三点共线 求参数 的值 利用共线向量定理及向量相等的条件列方程(组)求参数的值 ‎2．求解向量共线问题的注意事项 ‎(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用．‎ ‎(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．‎ ‎(3)若a与b不共线且λa＝μb，则λ＝μ＝0.‎ ‎(4)直线的向量式参数方程，A，P，B三点共线⇔＝(1－t)＋t (O为平面内任一点，t∈R)．‎ ‎(5)＝λ＋μ (λ，μ为实数)，若A，B，C三点共线，则λ＋μ＝1.‎ ‎[冲关演练]‎ ‎1．在四边形ABCD中，＝a＋2b，＝－‎4a－b，＝－‎5a－3b，则四边形ABCD的形状是(　　)‎ A．矩形　　　　　　　　　 B．平行四边形 C．梯形 D．以上都不对 解析：选C　由已知，得＝＋＋＝－‎8a－2b＝2(－‎4a－b)＝2，故∥.又因为与不平行，所以四边形ABCD是梯形．‎ ‎2．(2018·贵州适应性考试)已知向量e1与e2不共线，且向量＝e1＋me2，＝ne1＋e2，若A，B，C三点共线，则实数m，n满足的条件是(　　)‎ A．mn＝1 B．mn＝－1‎ C．m＋n＝1 D．m＋n＝－1‎ 解析：选A　因为A，B，C三点共线，所以一定存在一个确定的实数λ，使得＝λ eq o(AC,sup7(―→))，所以有e1＋me2＝nλe1＋λe2，由此可得所以mn＝1.‎ ‎(一)普通高中适用作业 A级——基础小题练熟练快 ‎1．设D，E，F分别为△ABC的三边BC，CA，AB的中点，则＋＝(　　)‎ A． 　　　　　　　　　　　 B. C. D． 解析：选A　由题意得＋＝(＋)＋(＋)＝(＋)＝.‎ ‎2．已知O是正六边形ABCDEF的中心，则与向量平行的向量为(　　)‎ A．＋ B．＋＋ C．＋＋ D．＋＋ 解析：选B　＋＋＝＝2＝－2.‎ ‎3．设向量a，b不共线，＝‎2a＋pb，＝a＋b，＝a－2b，若A，B，D三点共线，则实数p的值为(　　)‎ A．－2 B．－1‎ C．1 D．2‎ 解析：选B　因为＝a＋b，＝a－2b，所以＝＋＝‎2a－b.又因为A，B，D三点共线，所以，共线．设＝λ，所以‎2a＋pb＝λ(‎2a－b)，所以2＝2λ，p＝－λ，即λ＝1，p＝－1.‎ ‎4．下列四个结论：‎ ‎①＋＋＝0；②＋＋＋＝0；‎ ‎③－＋－＝0；④＋＋－＝0，‎ 其中一定正确的结论个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选C　①＋＋＝＋＝0，①正确；②＋＋＋＝＋MO―→＋＝，②错误；③－＋－＝＋＋＝＋＝0，③正确；④＋＋－＝＋＝0，④正确，故①③④正确．‎ ‎5．(2018·广东东莞二模)如图所示，已知＝3，＝a，＝b，＝c，则下列等式中成立的是(　　)‎ A．c＝b－a ‎ B．c＝2b－a C．c＝‎2a－b ‎ D．c＝a－b 解析：选A　因为＝3，＝a，＝b，所以＝＋＝＋＝＋(－)＝－＝b－a，故选A.‎ ‎6．设平行四边形ABCD的对角线交于点P，则下列命题中正确的个数是(　　)‎ ‎①＝＋；②＝(＋)；‎ ‎③＝－；④＝.‎ A．1 B．2‎ C．3 D．4‎ 解析：选C　由向量加法的平行四边形法则，知①＝＋，②＝(＋)都是正确的，由向量减法的三角形法则，知③＝－是正确的，因为， 的大小相同，方向相反，所以④＝是错误的．‎ ‎7．设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ＝________.‎ 解析：因为向量λa＋b与a＋2b平行，‎ 所以可设λa＋b＝k(a＋2b)，则所以λ＝.‎ 答案： ‎8．已知▱ABCD的对角线AC和BD相交于O，且＝a，＝b，则＝________，＝________.(用a，b表示)‎ 解析：如图，＝＝－＝b－a，＝－＝－－＝－a－b.‎ 答案：b－a　－a－b ‎9．(2018·河南三市联考)在锐角△ABC中，＝3，＝x＋y，则＝________.‎ 解析：由题设可得＋＝3(－)，‎ 即4＝3＋，‎ 亦即＝＋，‎ 则x＝，y＝，故＝3.‎ 答案：3‎ ‎10．已知S是△ABC所在平面外一点，D是SC的中点，若＝x＋y＋z，则x＋y＋z＝________.‎ 解析：依题意得＝－＝(＋)－＝－＋＋，因此x＋y＋z＝－1＋＋＝0.‎ 答案：0‎ B级——中档题目练通抓牢 ‎1．已知在等腰梯形ABCD中，AB∥CD，AB＝2CD，点M是腰BC的中点，若 ＝λ＋μ，则λ，μ的值分别为(　　)‎ A.， B.， C．1， D.， 解析：选A　因为＝(＋)＝(＋＋)＝(＋＋)＝＋，所以λ＝，μ＝.‎ ‎2．已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d共线反向，则实数λ的值为(　　)‎ A．1 B．－ C．1或－ D．－1或－ 解析：选B　由于c与d共线反向，则存在实数k使c＝kd(k＜0)，于是λa＋b＝k.‎ 整理得λa＋b＝ka＋(2λk－k)b.‎ 由于a，b不共线，所以有 整理得2λ2－λ－1＝0，解得λ＝1或λ＝－.‎ 又因为k＜0，所以λ＜0，故λ＝－.‎ ‎3．(2018·长春质检)在△ABC中，D为△ABC所在平面内一点，且＝＋，则＝(　　)‎ A. B. C. D. 解析：选B　如图，由已知得，点D在△ABC中与AB平行的中位线上，且在靠近BC边的三等分点处，从而有S△ABD＝S△ABC，S△ACD＝S△ABC，S△BCD＝S△ABC＝S△ABC，所以＝. ‎ ‎4．已知a，b是非零向量，命题p：a＝b，命题q：|a＋b|＝|a|＋|b|，则p是q的__________条件(选填“充要”“充分不必要”“必要不充分”“既不充分也不必要”)．‎ 解析：若a＝b，则|a＋b|＝|‎2a|＝2|a|，|a|＋|b|＝|a|＋|a|＝2|a|，即p⇒q.‎ 若|a＋b|＝|a|＋|b|，由加法的运算法则知a与b同向共线，‎ 即a＝λb，且λ>0，故q⇒/ p.‎ 所以p是q的充分不必要条件．‎ 答案：充分不必要 ‎5．在梯形ABCD中，已知AB∥CD，AB＝2CD，M，N分别为CD，BC的中点．若＝λ＋μ，则λ＋μ＝________.‎ 解析：法一：由＝λ＋μ，‎ 得＝λ·(＋)＋μ·(＋)，‎ 则＋＋＝0，‎ 得＋＋＝0，‎ 得＋＝0.‎ 又因为，不共线，‎ 所以由平面向量基本定理得 解得所以λ＋μ＝.‎ 法二：连接MN并延长交AB的延长线于点T，‎ 由已知易得AB＝AT，‎ ‎∴＝＝λ＋μ，‎ 即＝λ＋μ，‎ ‎∵T，M，N三点共线，∴λ＋μ＝1.∴λ＋μ＝.‎ 答案： ‎6.在△ABC中，D，E分别为BC，AC边上的中点，G为BE 上一点，且GB＝2GE，设＝a，＝b，试用a，b表示，.‎ 解：＝(＋)＝a＋b.‎ ＝＋＝＋＝＋(＋)‎ ‎＝＋(－)‎ ‎＝＋ ‎＝a＋b.‎ ‎7．设e1，e2是两个不共线的向量，已知＝2e1－8e2，＝e1＋3e2，＝2e1－e2.‎ ‎(1)求证：A，B，D三点共线；‎ ‎(2)若＝3e1－ke2，且B，D，F三点共线，求k的值．‎ 解：(1)证明：由已知得＝－＝(2e1－e2)－(e1＋3e2)＝e1－4e2，‎ ‎∵＝2e1－8e2，∴＝2.‎ 又∵与有公共点B，∴A，B，D三点共线．‎ ‎(2)由(1)可知＝e1－4e2，‎ ‎∵＝3e1－ke2，且B，D，F三点共线，‎ ‎∴存在实数λ，使＝λ，‎ 即3e1－ke2＝λe1－4λe2，‎ 得 解得k＝12.‎ C级——重难题目自主选做 ‎1.如图，直线EF与平行四边形ABCD的两边AB，AD分别交于E，F两点，且交其对角线于K，其中，＝，＝，＝λ，则λ的值为(　　)‎ A. B. C. D. 解析：选A　因为＝，＝，‎ 则＝，＝2，‎ 由向量加法的平行四边形法则可知＝＋，‎ 所以＝λ＝λ(＋)＝λ＝λ＋2λ，由E，F，K三点共线可得λ＋2λ＝1，所以λ＝.‎ ‎2．在直角梯形ABCD中，∠A＝90°，∠B＝30°，AB＝2，BC＝2，点E在线段CD上，若＝＋μ，则μ的取值范围是________．‎ 解析：由题意可求得AD＝1，CD＝，所以＝2.‎ ‎∵点E在线段CD上，‎ ‎∴＝λ (0≤λ≤1)．‎ ‎∵＝＋，‎ 又＝＋μ＝＋2μ＝＋ ，‎ ‎∴＝1，即μ＝.‎ ‎∵0≤λ≤1，‎ ‎∴0≤μ≤.‎ 即μ的取值范围是.‎ 答案： ‎(二)重点高中适用作业 A级——保分题目巧做快做 ‎1.设D，E，F分别为△ABC的三边BC，CA，AB的中点，则＋＝(　　)‎ A． 　　　　　　　　　　　B. C. D． 解析：选A　由题意得＋＝(＋)＋(＋)＝(＋)＝.‎ ‎2.(2018·合肥质检)已知O，A，B，C为同一平面内的四个点，若2＋＝0，则向量等于(　　)‎ A.－ B．－＋ C．2－ D．－＋2 解析：选C　因为＝－，＝－，所以2＋＝2(－)＋(－)＝－2＋＝0，所以＝2－.‎ ‎3.(2018·江西八校联考)在△ABC中，P，Q分别是边AB，BC上的点，且AP＝AB，BQ＝BC.若＝a，＝b，则＝(　　)‎ A.a＋b B．－a＋b C.a－b D．－a－b 解析：选A　＝＋＝＋＝＋(－)＝＋＝a＋b，故选A.‎ ‎4．下列四个结论：‎ ‎①＋＋＝0；②＋＋＋＝0；‎ ‎③－＋－＝0；④＋＋－＝0，‎ 其中一定正确的结论个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选C　①＋＋＝＋＝0，①正确；②＋＋＋＝＋＋＝，②错误；③－＋－＝＋＋＝＋‎ eq o(DC,sup7(―→))＝0，③正确；④＋＋－＝＋＝0，④正确．故①③④正确．‎ ‎5．已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d共线反向，则实数λ的值为(　　)‎ A．1 B．－ C．1或－ D．－1或－ 解析：选B　由于c与d共线反向，则存在实数k使c＝kd(k＜0)，于是λa＋b＝k.‎ 整理得λa＋b＝ka＋(2λk－k)b.‎ 由于a，b不共线，所以有 整理得2λ2－λ－1＝0，解得λ＝1或λ＝－.‎ 又因为k＜0，所以λ＜0，故λ＝－.‎ ‎6.(2018·南宁模拟)已知e1，e2是不共线向量，a＝me1＋2e2，b＝ne1－e2，且mn≠0，若a∥b，则＝________.‎ 解析：∵a∥b，∴a＝λb，即me1＋2e2＝λ(ne1－e2)，则故＝－2.‎ 答案：－2‎ ‎7．已知a，b是非零向量，命题p：a＝b，命题q：|a＋b|＝|a|＋|b|，则p是q的____________________条件(选填“充要”“充分不必要”“必要不充分”“既不充分也不必要”)．‎ 解析：若a＝b，则|a＋b|＝|‎2a|＝2|a|，|a|＋|b|＝|a|＋|a|＝2|a|，即p⇒q.‎ 若|a＋b|＝|a|＋|b|，由加法的运算法则知a与b同向共线，即a＝λb，且λ>0，故q⇒/ p.‎ 所以p是q的充分不必要条件．‎ 答案：充分不必要 ‎8．已知S是△ABC所在平面外一点，D是SC的中点，若＝x＋y＋z ‎，则x＋y＋z＝________.‎ 解析：依题意得＝－＝(＋)－＝－＋＋，因此x＋y＋z＝－1＋＋＝0.‎ 答案：0‎ ‎9.已知D为三角形ABC边BC的中点，点P满足＋＋＝0，＝λ，求实数λ的值．‎ 解：如图所示，由＝λ且＋＋＝0，得P为以AB，AC为邻边的平行四边形的第四个顶点，‎ 因此＝－2，所以λ＝－2.‎ ‎10．设e1，e2是两个不共线的向量，已知＝2e1－8e2，＝e1＋3e2，＝2e1－e2.‎ ‎(1)求证：A，B，D三点共线；‎ ‎(2)若＝3e1－ke2，且B，D，F三点共线，求k的值．‎ 解：(1)证明：由已知得＝－＝(2e1－e2)－(e1＋3e2)＝e1－4e2，‎ ‎∵＝2e1－8e2，‎ ‎∴＝2.‎ 又∵与有公共点B，‎ ‎∴A，B，D三点共线．‎ ‎(2)由(1)可知＝e1－4e2，‎ ‎∵＝3e1－ke2，且B，D，F三点共线，‎ ‎∴存在实数λ，使＝λ，‎ 即3e1－ke2＝λe1－4λe2，‎ 得 解得k＝12.‎ B级——拔高题目稳做准做 ‎1．(2018·长春质检)在△ABC中，D为△ABC所在平面内一点，且＝＋，则＝(　　)‎ A. B. C. D. 解析：选B　如图，由已知得，点D在△ABC中与AB平行的中位线上，且在靠近BC边的三等分点处，从而有S△ABD＝S△ABC，S△ACD＝S△ABC，S△BCD＝S△ABC＝S△ABC，所以＝. ‎ ‎2.(2018·河南中原名校联考)如图，在直角梯形ABCD中，AB＝2AD＝2DC，E为BC边上一点，＝3，F为AE的中点，则＝(　　)‎ A.－ B.－ C．－＋ D．－＋ 解析：选C　＝＋＝＋ ‎＝－＋(＋＋)‎ ‎＝－＋ ‎＝－＋＋＋(＋＋)‎ ‎＝－＋.‎ ‎3.在梯形ABCD中，已知AB∥CD，AB＝2CD，M，N分别为CD，BC的中点．若＝λ＋μ，则λ＋μ＝________.‎ 解析：法一：由＝λ＋μ，‎ 得＝λ·(＋)＋μ·(＋)，‎ 则＋＋＝0，‎ 得＋＋＝0，‎ 得＋＝0.‎ 又因为，不共线，‎ 所以由平面向量基本定理得 解得所以λ＋μ＝.‎ 法二：连接MN并延长交AB的延长线于T，‎ 由已知易得AB＝AT，‎ ‎∴＝＝λ＋μ，‎ 即＝λ＋μ，‎ ‎∵T，M，N三点共线，∴λ＋μ＝1.‎ ‎∴λ＋μ＝.‎ 答案： ‎4．在直角梯形ABCD中，∠A＝90°，∠B＝30°，AB＝2，BC＝2，点E在线段CD上，若＝＋μ，则μ的取值范围是________．‎ 解析：由题意可求得AD＝1，CD＝，所以＝2.‎ ‎∵点E在线段CD上，‎ ‎∴＝λ (0≤λ≤1)．‎ ‎∵＝＋，‎ 又＝＋μ＝＋2μ＝＋，‎ ‎∴＝1，即μ＝.‎ ‎∵0≤λ≤1，∴0≤μ≤.‎ 即μ的取值范围是.‎ 答案： ‎5．经过△OAB重心G的直线与OA，OB分别交于点P，Q，设＝m，＝n，m，n∈R，求＋的值．‎ 解：设＝a，＝b，则＝(a＋b)，‎ ＝－＝nb－ma，‎ ＝－＝(a＋b)－ma＝a＋b.‎ 由P，G，Q共线得，存在实数λ使得＝λ，‎ 即nb－ma＝λa＋λb，‎ 则消去λ，得＋＝3.‎ ‎6．已知O，A，B是不共线的三点，且＝m＋n(m，n∈R)．‎ ‎(1)若m＋n＝1，求证：A，P，B三点共线；‎ ‎(2)若A，P，B三点共线，求证：m＋n＝1.‎ 证明：(1)若m＋n＝1，‎ 则＝m＋(1－m) ‎＝＋m(－)，‎ ‎∴－＝m(－)，‎ 即＝m，∴与共线．‎ 又∵与有公共点B，‎ ‎∴A，P，B三点共线．‎ ‎(2)若A，P，B三点共线，‎ 则存在实数λ，使＝λ，‎ ‎∴－＝λ(－)．‎ 又＝m＋n.‎ 故有m＋(n－1)＝λ－λ，‎ 即(m－λ)＋(n＋λ－1)＝0.‎ ‎∵O，A，B不共线，∴，不共线，‎ ‎∴∴m＋n＝1.‎