- 2021-06-23 发布 |
- 37.5 KB |
- 4页

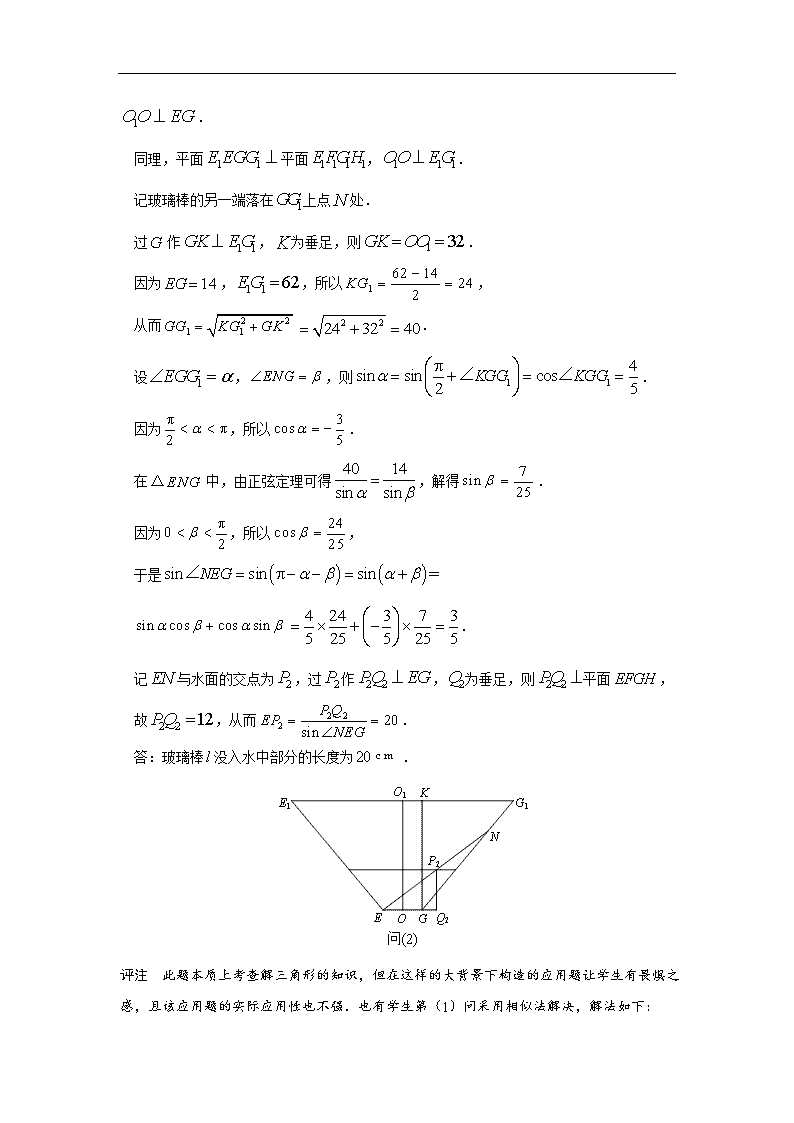
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013-2017高考数学分类汇编-第8章 立体几何-3 空间点,直线,平面之间的位置关系(理科)
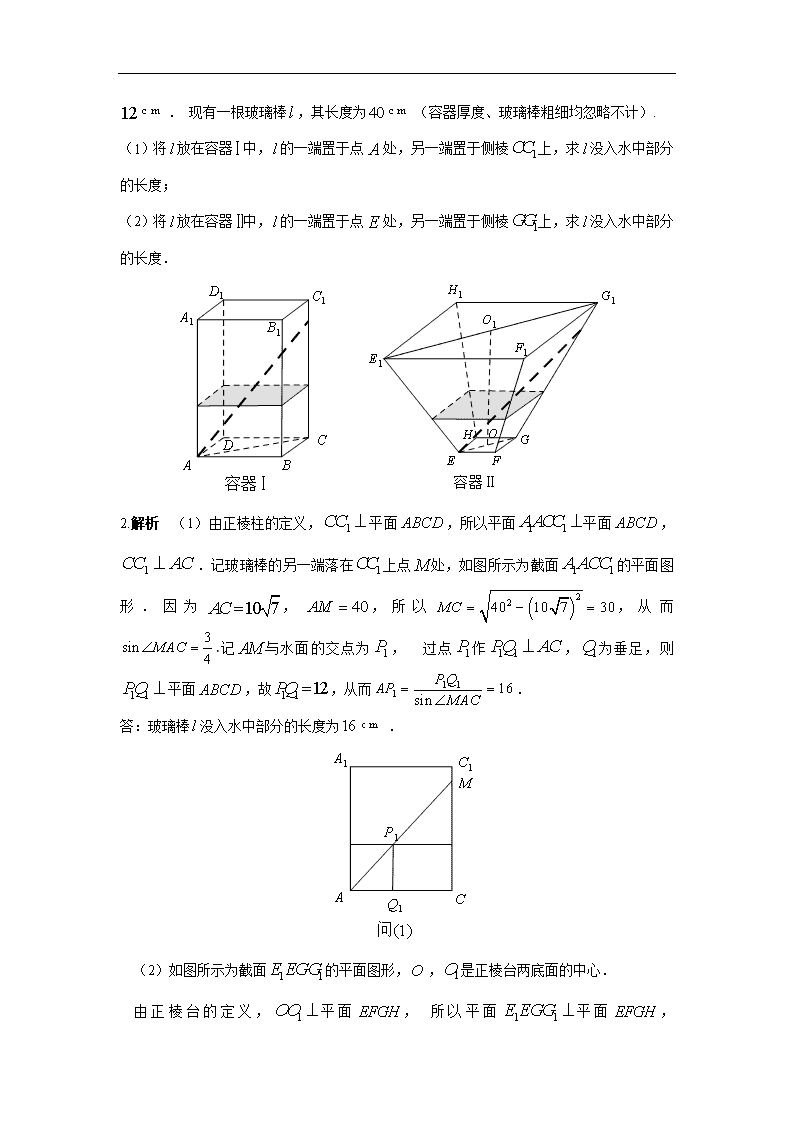
第3节 空间点、直线、平面之间的位置关系 1.已知直线,分别在两个不同的平面,内,则“直线和直线相交”是“平面和平面相 交”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 1.A 解析 由直线和直线相交,可知平面有公共点,所以平面和平面相交.反过来,如果平面和平面相交,直线和直线不一定相交,可能与两平面的交线都平行.故选A. 题型90 证明“点共面”“线共面”“点共线”或“线共点” ——暂无 1. (2013安徽理3) 在下列命题中,不是公理的是( ). A. 平行于同一个平面的两个平面相互平行 B. 过不在同一条直线上的三点,有且只有一个平面 C. 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 D. 如果两个不重合的平面有一个公共点,那么他们有且只有一条过该点的公共直线 题型91 截面问题——暂无 1. (2013安徽理15) 如图,正方体的棱长为,为的中点,为线段上的动点,过点的平面截该正方体所得的截面记为.则下列命题正确的是 (写出所有正确命题的编号) ①当时,为四边形 ②当时,为等腰梯形 ③当时,与的交点满足 ④当时,为六边形 ⑤当时,的面积为 2.(2017江苏18)如图所示,水平放置的正四棱柱形玻璃容器和正四棱台形玻璃容器的高均为,容器的底面对角线的长为,容器的两底面对角线,的长分别为和. 分别在容器和容器中注入水,水深均为 . 现有一根玻璃棒,其长度为(容器厚度、玻璃棒粗细均忽略不计). (1)将放在容器中,的一端置于点处,另一端置于侧棱上,求没入水中部分 的长度; (2)将放在容器中,的一端置于点处,另一端置于侧棱上,求没入水中部分 的长度. 2.解析 (1)由正棱柱的定义,平面,所以平面平面,.记玻璃棒的另一端落在上点处,如图所示为截面的平面图形.因为,,所以,从而.记与水面的交点为, 过点作,为垂足,则平面,故,从而. 答:玻璃棒没入水中部分的长度为. (2)如图所示为截面的平面图形,,是正棱台两底面的中心. 由正棱台的定义,平面, 所以平面平面, . 同理,平面平面,. 记玻璃棒的另一端落在上点处. 过作,为垂足,则. 因为,,所以, 从而. 设,,则. 因为,所以. 在中,由正弦定理可得,解得. 因为,所以, 于是 . 记与水面的交点为,过作,为垂足,则平面, 故,从而. 答:玻璃棒没入水中部分的长度为. 评注 此题本质上考查解三角形的知识,但在这样的大背景下构造的应用题让学生有畏惧之感,且该应用题的实际应用性也不强.也有学生第(1)问采用相似法解决,解法如下: ,,所以,, 所以由,,即,解得. 答:玻璃棒没入水中部分的长度为. 题型92 异面直线的判定——暂无 1.(2015年广东理8)若空间中个不同的点两两距离都相等,则正整数的取值( ) A.至多等于 B.至多等于 C.等于 D.大于 1.解析 正四面体的四个顶点两两距离相等,即空间中个不同的点两两距离都相等, 则正整数可以等于4,而且至多等于4.假设可以等于5,则不妨先取出其中4个点,为,,,,则构成一个正四面体的四个顶点,设第5个点为点,则点和点,,也要构成一个正四面体,此时点要么跟点重合,要么点和点关于平面对称,但此时的长又不等于,故矛盾.故选B.查看更多