- 2021-06-23 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
福建省三明一中2019-2020学年高二上学期第二次月考数学答案
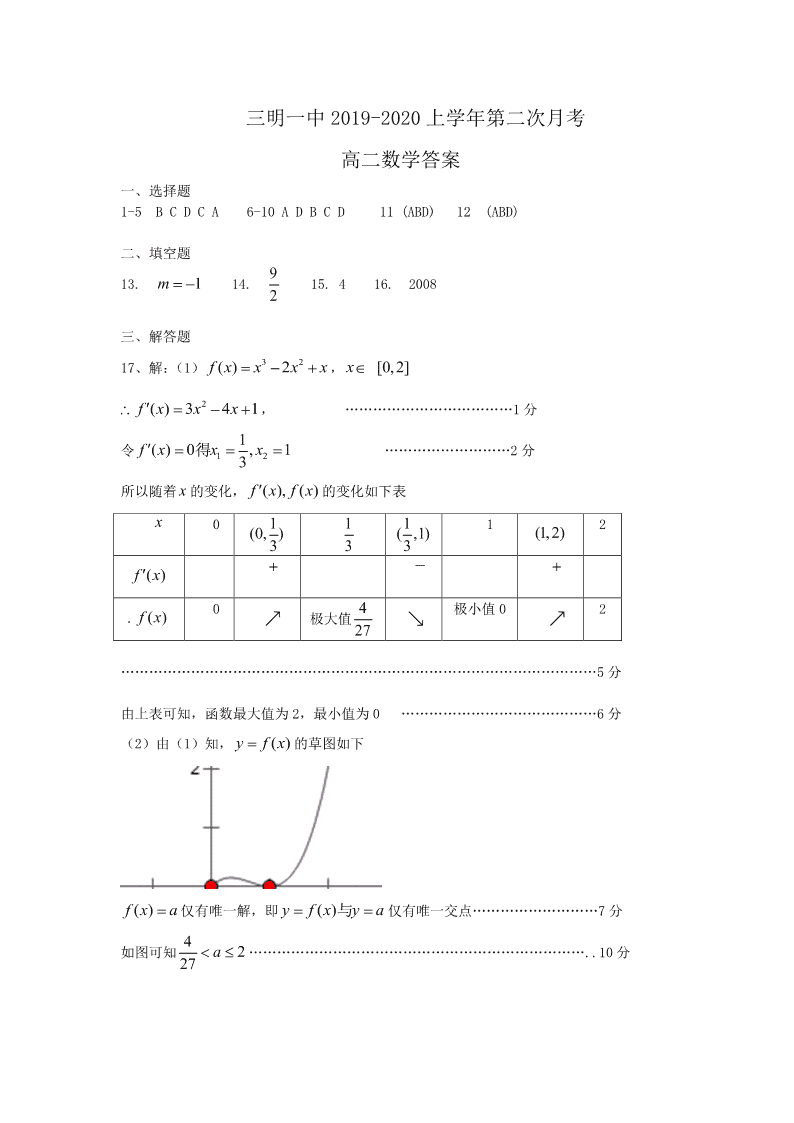
三明一中 2019-2020 上学年第二次月考 高二数学答案 一、选择题 1-5 B C D C A 6-10 A D B C D 11 (ABD) 12 (ABD) 二、填空题 13. 1m 14. 9 2 15. 4 16. 2008 三、解答题 17、解:(1) 32( ) 2f x x x x , x [0,2] 2( ) 3 4 1f x x x , ………………………………1 分 令 12 1( ) 0 , 13f x x x 得 ………………………2 分 所以随着 x 的变化, ( ), ( )f x f x 的变化如下表 x 0 1(0, )3 1 3 1( ,1)3 1 (1,2) 2 ()fx _ . ()fx 0 极大值 4 27 极小值 0 2 …………………………………………………………………………………………5 分 由上表可知,函数最大值为 2,最小值为 0 ……………………………………6 分 (2)由(1)知, ()y f x 的草图如下 ()f x a 仅有唯一解,即 ()y f x y a与 仅有唯一交点………………………7 分 如图可知 4 227 a………………………………………………………………..10 分 18.解(1)方程 22 113 xy kk 表示椭圆 即椭圆标准方程为 22 113 xy kk ,…………………………………2 分 所以只需要 1 0, 1kk 即 …………………………………4 分 故 p 为真命题时, 1k ……………………………………………………….5 分 (2) 2, 1 0x R kx kx 恒成立 则可知 ① 当 0k 时,不等式成立 ………………………………………6 分 ②当 2 00 040 40 kk k kk ………………………8 分 综上可知04k 命题 :0 4qk ……………………………………………9 分 由已知可知, p为假,命题 q为真 ………………………………………10 分 即 1 1404 k kk ……………………………………………12 分 19. 解 (1)直线 AB 的方程是 y=2 (x-p 2),与 y2=2px 联立, 从而有 4x2-6px+p2=0 ………………………………………………………….2 分 所以 12 3 2x x p , ……………………………………………………………..3 分 由抛物线定义得 |AB|= 12 5 52x x p p , …………………………………………………5 分 所以 p=2,从而抛物线方程为 y2=4x …………………………………………6 分 (2)由于 p=2,则 直线 AB: 22yx,即 2 2 0xy 由已知OC OA OB,所以四边形OACB 为平行四边形 ………………7 分 2OACB OABS S AB d (其中 d 为O 到直线 AB 的距离) ……………8 分 又 22 2 0 0 2 2 52 ( 1) d ………………………………………………….10 分 2 5 2 5 5OABCS …………………………………………………………….12 分 20 解:(1) 2( ) ln 2 , 0f x x x x x 1( ) 2 2f x xx ……………………………………2 分 故 (1) 1, (1) 1ff,即切点为(1,1),切线的斜率为 1……………4 分 所以所求的切线方程为 0xy…………………………………………5 分 (2) 2( ) ln , 0f x x ax x x ,即 ln xax x 设 ln() xg x x x ,则 min()a g x ………………………6 分 又 2 2 ln 1() xxgx x ……………………………………7 分 设 2( ) ln 1h x x x ,则易知 单调递增………………8 分 由 (1) 0,h 可知 (0,1), ( ) 0; (1, ), ( ) 0x h x x h x ……………………9 分 即 (0,1), ( ) 0; (1, ), ( ) 0x g x x g x 所以 在(0,1) 上单调递减,在(1, ) 时单调递增…………11 分 即 min( ) (1) 1g x g,所以 1a ………………………………………………12 分 21 (1)证明 ∵ DC=BC=1,DC⊥BC,∴BD= 2,……………………………1 分 又 AD= 2,AB=2,∴AD2+BD2=AB2, ∴∠ADB=90°,∴AD⊥BD…………………………………………………………..2 分 又平面 ADEF⊥平面 ABCD,平面 ADEF∩平面 ABCD=AD, ∴BD⊥平面 ADEF,----------------------------------------------------------------------------4 分 又 BD⊂平面 BDM, ∴平面 BDM⊥平面 ADEF.---------------------------------------------------------------------5 分 (2)解 在平面 DAB 内过点 D 作 DN⊥AB,垂足为 N, ∵AB∥CD,∴DN⊥CD, 又平面 ADEF⊥平面 ABCD,平面 ADEF∩平面 ABCD=AD,DE⊥AD, ∴ED⊥平面 ABCD,∴DN⊥ED, 以 D 为坐标原点,DN 所在的直线为 x 轴,DC 所在的直线为 y 轴,DE 所在的直线为 z 轴, 建立空间直角坐标系如图所示.……………………………………………………6 分 ∴B(1,1,0),C(0,1,0),E(0,0, 2),N(1,0,0),………………………………….7 分 设 M(x0,y0,z0),EM→ =λEC→(0≤λ<1), ∴(x0,y0,z0- 2)=λ(0,1,- 2), ∴x0=0,y0=λ,z0= 2(1-λ), ∴M(0,λ, 2(1-λ)).……………………………………………………………….8 分 设平面 BDM 的法向量为 n1=(x,y,z), 则 n1·DM→ =0, n1·DB→ =0, 又DM→ =(0,λ, 2(1-λ)),DB→ =(1,1,0),…………………………………………..9 分 ∴ λy+ 21-λz=0, x+y=0, 令 x=1,得 y=-1,z= λ 21-λ, 故 n1=(1,-1, λ 21-λ)是平面 BDM 的一个法向量.------------------------10 分 ∵平面 ABF 的一个法向量为DN→ =(1,0,0),-------------------------------------------11 分 ∴|cos〈n1,DN→ 〉|= 1 1+1+ λ2 21-λ2 =1 2,得 λ=2 3, ∴M(0,2 3, 2 3 ), ∴点 M 在线段 CE 的三等分点且靠近点 C 处.---------------------------------------12 分 22. 综上可知 ()fx在区间[0,1] 上只有唯一的零点 …………………………12 分查看更多