2020届二轮复习平面向量的实际背景及基本概念课件（10张）（全国通用）

2020届二轮复习平面向量的实际背景及基本概念课件（10张）（全国通用）

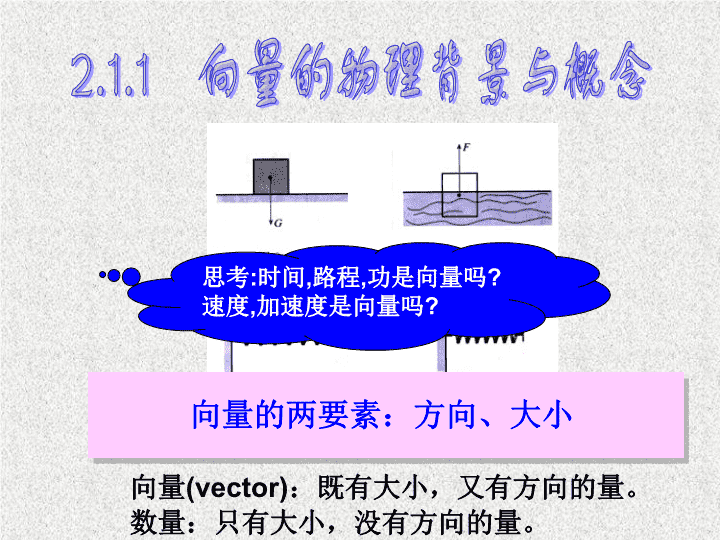
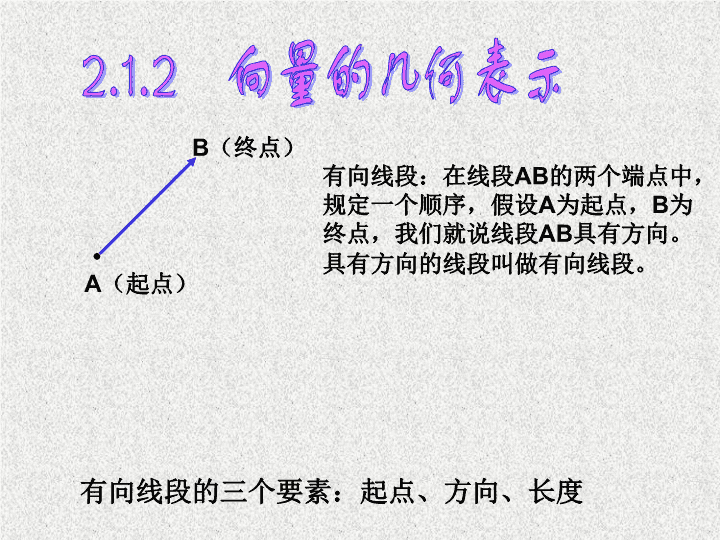
2.1.1 向量的物理背景与概念 向量 (vector) ：既有大小，又有方向的量。 数量 ：只有大小，没有方向的量。 思考 : 时间 , 路程 , 功是向量吗 ? 速度 , 加速度是向量吗 ? 向量的两要素：方向、大小 2.1.2 向量的几何表示 由于实数与数轴上的点一一对应，所以 数量 常常用数轴上的一个点表示，如 3 ， 2 ， -1 ， … 而且不同的点表示不同的数量。 对于 向量 ，我们常用带箭头的线段来表示，线段按一定比例（标度）画出，它的长度表示向量的大小，箭头表示向量的方向。 0 1 2 3 -1 有向线段： 在线段 AB 的两个端点中，规定一个顺序，假设 A 为起点， B 为终点，我们就说线段 AB 具有方向。具有方向的线段叫做有向线段。 有向线段的三个要素： 起点、方向、长度 A （起点） B （终点） 2.1.2 向量的几何表示 1 、向量的几何表示 ：用有向线段表示。 2.1.2 向量的几何表示 思考 : “ 向量就是有向线段 , 有向线段就是向量 .” 的说法对吗 ? 向量 AB 的大小，也就是向量 AB 的 长度 （或称 模 ），记作 |AB| 。 长度为 0 的向量叫做 零向量 ，记作 0 。 长度等于 1 个单位的向量，叫做 单位向量 。 2 、向量的字母表示 ：（ 1 ） a , b , c , . . . （ 2 ）用表示向量的有向线段的起点和终点字母 表示，例如， AB ， CD 1. 温度含零上和零下温度，所以温度是向量（ ） 判断题 × × 2. 向量的模是一个正实数。（　　 ） × 注 : 向量不能比较大小 2.1.2 向量的几何表示 长度相等且方向相同的两个向量表示相等向量， 但是两个向量之间 只有相等关系 ，没有大小之分， “ 对于向量 ， ， ＞ ，或 ＜ ” 这种说法是错误的 . 3. 若 |a|>|b| ，则 a > b ( ) 平行向量又叫做共线向量 各向量的终点与直线 l 之间有什么关系？ 如： a b c （１） 平行向量： 方向 相同 或 相反 的 非零向量 叫做平行向量 (parallel vectors) 。 记作 a ∥b ∥c 规定： 0 与任一向量平行。 问： 把一组平行于直线 l 的向量的起点平移到直线 l 上的 一点 O ，这时它们是不是平行向量？ o l . C OC = c A OA = a OB = b B 2.1.3 相等向量与共线向量 向量相等 向量 平行 平行向量一定是相等向量吗 ? ? 相等向量一定是平行向量吗 ? （ 2 ） 相等向量： 长度 相等 且 方向相同 的向量叫做相等向量。 记作： a = b 规定： 0 = 0 a b ？ 1. 若非零向量 AB//CD ，那么 AB//CD 吗？ 2. 若 a//b , 则 a 与 b 的方向一定相同或相反吗？ o . b a A B C D D C B A 2.1.3 相等向量与共线向量 11 个 例 1 ．如图设 O 是正六边形 ABCDEF 的中心，写出图中  与向量 OA 相等的向量。 OA = DO = CB 变式一：与向量 OA 长度相等的向量 有多少个？ 变式二：是否存在与向量 OA 长度相等，方向 相反的向量？ 存在，为 FE CB 、 DO 、 FE 变式三：与向量 OA 长度 相等的 共线向量有哪些？ 2.1.3 相等向量与共线向量 课堂讨论 1. 判断下列命题是否正确，若不正确，请简述理由 .  ① 向量 与 是共线向量，则 A 、 B 、 C 、 D 四点必在一直线上； ②单位向量都相等； ③任一向量与它的相反向量 ( 长度相同 , 方向相反的向量 ) 不相等；  ④共线的向量，若起点不同，则终点一定不同。 (×) (×) (×) (×) 2. 下面几个命题： C （ 3 ）若 |a|=|b| ，则 a = b （ 2 ）若 |a|=0 ，则 a = 0 |a|=|b| a ∥ b （ 4 ）两个向量 a 、 b 相等的充要条件是 （ 1 ）若 a = b ， b = c ，则 a = c 。 当 b ≠ 0 时成立。 问：若 a ∥ b ， b ∥ c, 则 a ∥c A ． 0 　　 B. 1 C. 2 D. 3 其中正确的个数是 ( ) （ 5 ）若 A 、 B 、 C 、 D 是不共线的四点，则 AB=DC 是 四边形 ABCD 是平形四边形的等价条件。 A B D C B A C D 课堂讨论