- 2021-06-23 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届辽宁省沈阳铁路实验中学高三10月月考(2017
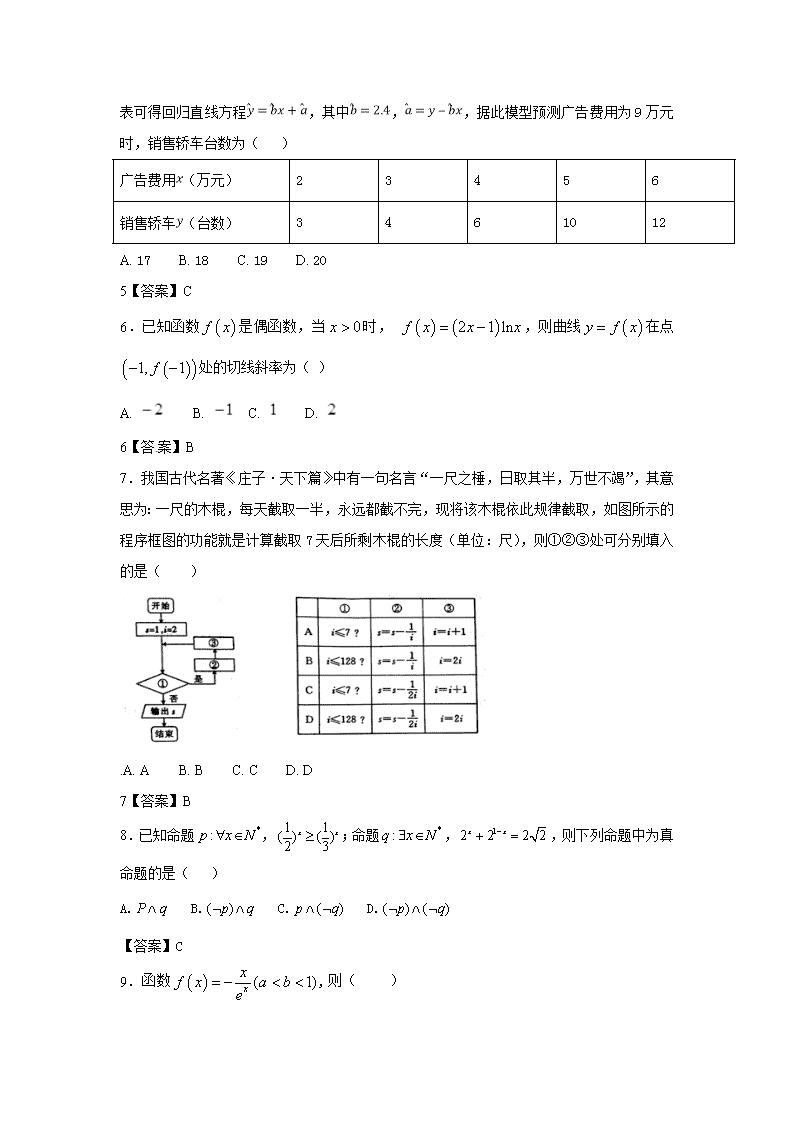
沈阳铁路实验中学2017-2018年高三第一次月考 数 学(理) 命题人:殷裕民 本试卷分第Ⅰ卷和第Ⅱ卷两部分。满分150分,考试时间120分钟。 注意事项: 1.答第Ⅰ卷前,考生务必将自己的姓名、考号填写在答题卡上。 2.单项选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦 干净后,再选涂其它答案标号,答在试卷上无效。其它试题答在答题卡上。 3.考试结束后,考生将答题卡交回。【来源:全,品…中&高*考+网】 第Ⅰ卷 一、选择题(共12小题,每小题5分,共计60分) 1.已知集合, ,则 ( ) A. B. C. D. 1【答案】C 2.已知复数的实部和虚部相等,则 A. B. C. D. 2【答案】D 3.使不等式2x2-5x-3≥0成立的一个充分而不必要条件是( ) A. x<0 B. x≥0 C. x∈{-1,3,5} D. x≤-或x≥3 3【答案】C 4.若,则=( ) A. 1 B. C. D. 【答案】D 5. 某厂家为了解销售轿车台数与广告宣传费之间的关系,得到如表统计数据表:根据数据表可得回归直线方程,其中,,据此模型预测广告费用为9万元时,销售轿车台数为( ) 广告费用(万元) 2 3 4 5 6 销售轿车(台数) 3 4 6 10 12 A. 17 B. 18 C. 19 D. 20 5【答案】C 6.已知函数是偶函数,当时, ,则曲线在点处的切线斜率为( ) A. B. C. D. 6【答案】B 7.我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( ) .A. A B. B C. C D. D 7【答案】B 8.已知命题,;命题,,则下列命题中为真命题的是( ) A. B. C. D. 【答案】C 9.函数,则( ) A. B. C. D. 的大小关系不能确定 9【答案】C 10.函数的定义域和值域都是,则( ) A. 1 B. 2 C. 3 D. 4 10【答案】C【来源:全,品…中&高*考+网】 【解析】试题分析:当时,函数是单调递减函数,,解得,当时,函数是单调递增函数不成立,所以,那么,故选C. 考点:1.指数函数;2.对数. 11.已知与都是定义在上的奇函数,且当时, (),若恰有4个零点,则正实数的取值范围是( ) A. ; B. ; C. ; D. . 11【答案】C 12.已知定义在上的函数满足条件,且函数是偶函数,当时, (),当时, 的最小值为3,则a的值等于( ) A. B. e-2 C. 2 D. 1 12【答案】A 第II卷 二、填空题(共4小题,每小题5分,共计20分) 13.__________. 13【答案】 14.若函数是奇函数,则使成立的的取值范围是__________. 14【答案】 15.已知实数a≠1,函数f(x)=,若f(1﹣a)=f(a﹣1),则a的值为 . 16.如果对定义在上的函数,对任意两个不相等的实数都有,则称函数为“函数”. 下列函数①;②;③;④ 是“函数”的所有序号为_______. 16【答案】①③ 三、解答题(共6题,总计70分) 17.已知函数的定义域为. (1)求; (2)当时,求的最小值. 17【答案】(1);(2). 18.近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出次成功交易,并对其评价进行统计爱,商品和服务评价的列联表如下表: 对服务好评 对服务不满意 合计 对商品好评 对商品不满意 合计 (1)是否可以在犯错误概率不超过的前提下,认为商品好评与服务好评有关? (2)若将频率视为概率,某人在该购物平台上进行的次购物中,设对商品和服务全好评的次数为随机变量,求的数学期望. 参考数据: 【来源:全,品…中&高*考+网】 (,其中) 18【答案】(1)可以(2)见解析 【解析】试题分析:(1)由已知列出关于商品和服务评价的2×2列联表,代入公式求得k2的值,对应数表得答案; (2)每次购物时,对商品和服务全好评的概率为0.4,且X的取值可以是0,1,2,3,X~B(3,0.4).求出相应的概率,可得对商品和服务全好评的次数X的分布列(概率用组合数算式表示);利用二项分布的数学期望和方差求X的数学期望. 试题解析: 解:(1) ,可以在犯错误概率不超过的前提下,认为商品好评与服务好评有关. (2)由题意的取值可以是.每次购物时,对商品和服务都好评的概率为 所以; ; ; . 的分布列为: 所以. 19.已知c>0,命题p:函数在R上单调递减,命题q:不等式的解集是R,若为真命题, 为假命题,求c的取值范围。 19【答案】 【解析】试题分析: 分类讨论p真q假和p假q真两种情况,可得c的取值范围是. 试题解析: 由已知得:p,q两个命题有且只有一个命题为真命题。有下列两种情形: (i)p真q假 (ii)p假q真。 当p为真命题时:根据指数函数的性质得:0查看更多