数学理卷·2018届广东汕头市高三普通高中毕业班教学质量监测试题（2018

数学理卷·2018届广东汕头市高三普通高中毕业班教学质量监测试题（2018

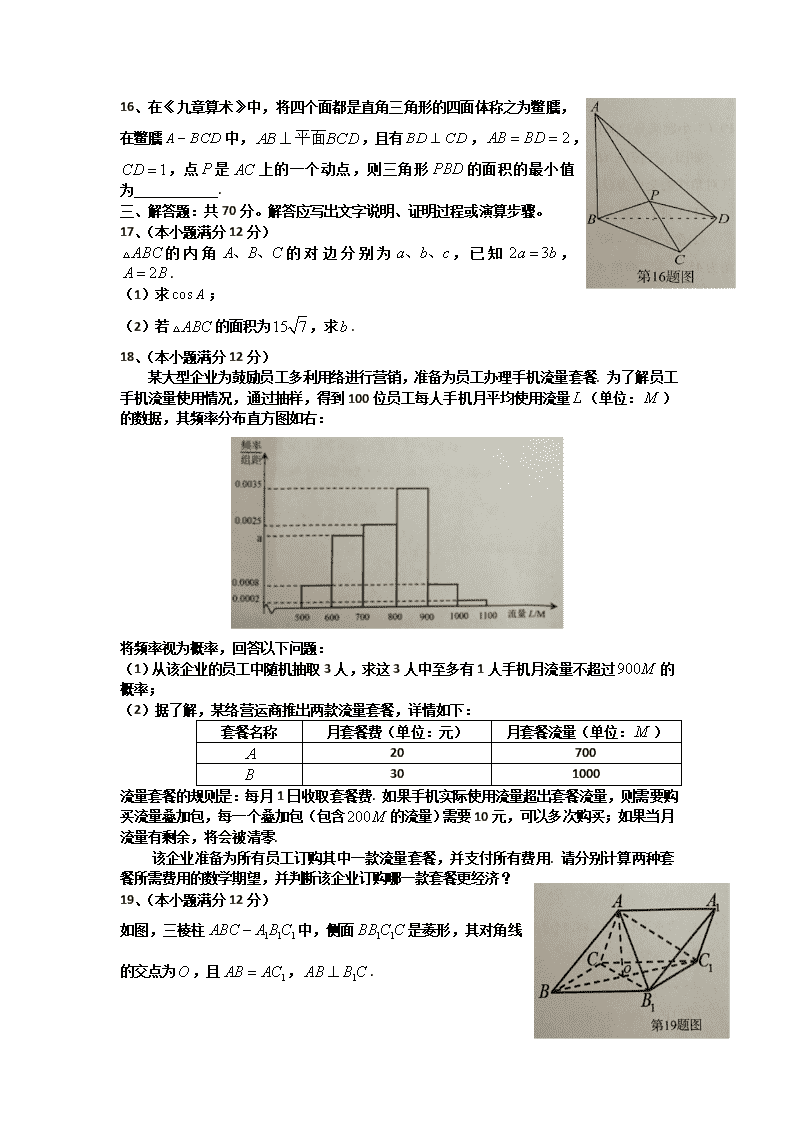
汕头市2017-2018学年度普通高中毕业班教学质量监测试题 理科数学 注意事项：‎ 1、 答卷前，考生务心用黑色字迹的钢笔或签字笔将自己的姓名、学校、座位号、考生号填写在答题卡上. ‎ 2、 选择题每小题选出答案后，用铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.‎ 3、 非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液. 不按以上要求作答的答案无效.‎ 4、 作答选做题时，请先用铅笔填涂选做题的题号对应的信息点，再作答. 漏涂、错涂、多涂的，答案无效.‎ 5、 考生必须保持答题卡的整洁. 考试结束后，将试卷和答题卡一并交回.‎ 第Ⅰ卷（共60分）‎ 一、 选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合要求的。‎ 1、 已知集合，则（ ）‎ ‎ . . . .‎ 2、 已知是复数的共轭复数，若，则复数对应的点位于（ ）‎ ‎.第一象限 .第二象限 .第三象限 .第四象限 3、 若两个非零向量满足，，则的夹角是（ ）‎ ‎. . . .‎ 4、 记为等差数列的前项和，，则的值为（ ）‎ ‎. . . .‎ 5、 执行右图的程序框图，如果输入的，则输出的（ ）‎ ‎. . . .‎ 6、 已知命题关于的方程没有实根；命题.若“”和“”都是假命题，则实数的取值范围是（ ）‎ ‎. . . .‎ 1、 某电商设计了一种红包，打开每个红包都会获得三种福卡（“和谐”、“爱国”、“敬业”）中的一种，若集齐三种卡片可获得奖励，小明现在有4个此类红包，则他获奖的概率为（ ）‎ ‎. . . .‎ 2、 将偶函数的图像向右平移个单位得到函数的图像，则在上的最小值是（ ）‎ ‎. . . .‎ 3、 某多面体的三视图如图所示，则该多面体的各个三角形面中，最大面积为（ ）‎ ‎ . . . .‎ 4、 已知圆锥的母线长为，它的底面圆周和顶点都在一个表面积为的球面上，则该圆锥的体积为（ ）‎ ‎. . . .‎ 5、 已知函数，则不等式的解集为（ ）‎ ‎ . . . .‎ 6、 已知函数有两个零点，则实数的取值范围是（ ）‎ ‎. . . .‎ 第Ⅱ卷（共90分）‎ 一、 填空题：本题共4小题，每小题5分，共20分。‎ 13、 已知实数满足，则目标函数的最大值为 .‎ 14、 展开式中，含项的系数是 .（用数字填写答案）‎ 15、 数列中，，，其中满足：对于任意的，均有成等差. 数列的前20项和 .‎ 13、 在《九章算术》中，将四个面都是直角三角形的四面体称之为鳖臑，在鳖臑中，，且有，，，点是上的一个动点，则三角形的面积的最小值为 .‎ 一、 解答题：共70分。解答应写出文字说明、证明过程或演算步骤。‎ 17、 ‎（本小题满分12分）‎ 的内角的对边分别为，已知，.‎ （1） 求；‎ （2） 若的面积为，求.‎ 18、 ‎（本小题满分12分）‎ 某大型企业为鼓励员工多利用络进行营销，准备为员工办理手机流量套餐. 为了解员工手机流量使用情况，通过抽样，得到100位员工每人手机月平均使用流量（单位：）的数据，其频率分布直方图如右：‎ 将频率视为概率，回答以下问题：‎ （1） 从该企业的员工中随机抽取3人，求这3人中至多有1人手机月流量不超过的概率；‎ （2） 据了解，某络营运商推出两款流量套餐，详情如下：‎ 套餐名称 月套餐费（单位：元）‎ 月套餐流量（单位：）‎ ‎20‎ ‎700‎ ‎30‎ ‎1000‎ 流量套餐的规则是：每月1日收取套餐费. 如果手机实际使用流量超出套餐流量，则需要购买流量叠加包，每一个叠加包（包含的流量）需要10元，可以多次购买；如果当月流量有剩余，将会被清零.‎ 该企业准备为所有员工订购其中一款流量套餐，并支付所有费用. 请分别计算两种套餐所需费用的数学期望，并判断该企业订购哪一款套餐更经济？‎ 19、 ‎（本小题满分12分）‎ 如图，三棱柱中，侧面是菱形，其对角线的交点为，且，. ‎ （1） 求证：；‎ ‎（2）设，若直线与平面所成的角为，求二面角的大小.‎ 20、 ‎（本小题满分12分）‎ 已知椭圆的离心率为，短轴长为，左右顶点分别为，点是椭圆上异于的任意一点，记直线的斜率分别为. ‎ （1） 求椭圆的方程，并证明：是定值；‎ （2） 设点是椭圆上另一个异于的点，且满足直线的斜率等于，试探究：直线是否经过定点？如果是，求出该定点，如果不是，请说明理由.‎ 21、 ‎（本小题满分12分）‎ 已知函数.‎ （1） 讨论的单调性；‎ （2） 当时，，求的取值范围.‎ 请考生在第22，23题中任选一题作答. 作答时一定要用铅笔在答题卡上把所选题目对应的题号涂黑（都没涂黑的视为选做第22题）.‎ 22、 ‎（本小题满分10分）选修：坐标系与参数方程 在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的极坐标方程为.‎ （1） 求曲线和直线的交点的极坐标；‎ （2） 已知为曲线上的一动点，设直线与曲线的交点为，求面积的最小值.‎ 23、 ‎（本小题满分10分）选修：不等式选讲 已知函数 （1） 当时，解不等式；‎ （2） 求函数的最小值.‎ 汕头市2017~2018学年度普通高中毕业班第一学期 统一监测试题理科数学参考答案 一、选择题.‎ BBDAB CCACB CA 二、填空题.‎ ‎13. 14. 15. 16. ‎ ‎16.作于，于 易证，，‎ 得，‎ 因此 设，则 所以时， ‎ 三、解答题.‎ ‎17.（1）由正弦定理得……1分 ‎， ……2分 ‎， ……3分 ‎ ……4分 ……5分 ‎（2），……6分 ……7分 ‎……8分 ‎ ……9分 ‎……10分 得到……11分 又，可得. ……12分 ‎18. （1）依题意，，……1分 得 ……2分 从该企业的员工中随机抽取3人，可近似的看为独立重复实验，每人手机月流量不超过900M的概率为，……3分 至多1人可分为恰有一人和0人手机月流量不超过900M，‎ 设事件A为“3人中至多有1人手机月流量不超过900M” ，……4分 则……5分 ‎ （2）若该企业选择A套餐，设一个员工的所需费用为，则可能为……6分 的分布列为 X ‎20‎ ‎30‎ ‎40‎ P ‎……7分 ‎……8分 若该企业选择B套餐，设一个员工的所需费用为，则可能为……9分 的分布列为 Y ‎30‎ ‎40‎ P ‎……10分 ‎……11分 订购A套餐更经济. ……12分 第19题图 x z y ‎19.（1）四边形是菱形 ……1分 ‎，且 ‎ ‎ 平面 ……2分 ‎……3分 ‎， 是的中点，……4分 又， 平面……5分 ‎（2）（法一）‎ 直线与平面的所成角等于直线与平面的所成角 平面 直线与平面的所成角为，……6分即 不妨设菱形的边长为2，则在等边三角形中，‎ 在直角三角形中，……7分 以为原点建立空间直角坐标系，则……8分 设平面的一个法向量为 则得……9分 而平面的一个法向量为……10分 ‎……11分 二面角的大小为. ……12分 ‎（法二）‎ 不妨设菱形的边长为2，则在等边三角形中，‎ 设 以为原点建立空间直角坐标系，则……6分 ‎ 平面的法向量为 依题意有，，……7分 得到……8分 因此， ‎ 设平面的一个法向量为 则得……9分 而平面的一个法向量为……10分 ‎……11分 二面角的大小为. ……12分 ‎20. （1）依题意有，……1分 解得 ……2分 椭圆的方程为，……3分，设 则……4分 ……5分 ‎（2）（法一），，……6分 即 设的方程为，，‎ ‎……7分 则，……8分 ‎……9分 得 ‎……10分 化简得，或……11分 即的方程为或，‎ 因为经过右顶点，舍去；所以直线经过定点……12分 ‎（法二），，……6分即 当轴时，直线方程为……7分 的斜率存在时，设的方程为，，‎ ‎，……8分 则，‎ ‎……9 分 得……10分 化简得,或……11分 即的方程为或，‎ 因为经过右顶点，舍去；所以直线经过定点……12分 ‎（法三）设的方程为 ‎，……6分 ‎，……7分得，‎ 设的方程为 ‎， ‎ ‎，得，……8分 ‎，……9分 ‎……10分 直线的方程为 ……11分 即 所以直线经过定点.……12分 ‎21（1） ……1分 时，，在上递增 ……2分 时，由得，……3分 ‎，，在上递减 ；，，在上递增 ……4分 ‎（2）变形为 令, ‎ 令，可得 ……5分 令， ……6分 时，，在上单调递增 ……7分 的值域是 ……8分 当时，没有实根，，……9分 在上单调递增, ，符合题意. ……10分 当时，有唯一实根，时，，……11分 ‎ ‎ 在上递减， ，不符题意. ……12分 综上，的取值范围是. ‎ ‎22（1）曲线转化为直角坐标：，，……1分 即 ‎ 直线转化为直角坐标：，即 ……2分 联立得到曲线和直线的交点，……3分……4分 它们的极坐标为.（注：也可以）……5分 ‎（2）由（1）得，……6分 因此，的面积取得最小时也就是到直线的距离最小的时候 设 则到直线的距离……7分……8分 当时，取得最小值……9分 因此的面积的最小值为……10分 ‎23（1）当时, ……1分 时，，得，即有……2分 时，，得，即有……3分 时，，得，即有……4分 综上，不等式的解集为R. ……5分 ‎（2）……6分 ‎ ‎ ‎……7分 ‎……8分 ‎……9分 当且仅当且时取“=”‎ 函数的最小值为……10分